 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Rodrigo
Join Date: Mar 2020
Posts: 9
Rep Power: 6  |
Hi everyone
I found an equation of numerical integration over of control volume: 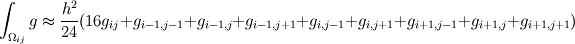 I am wondering why it is 16/24 and 1/24. I would like to get the formula for 3D numerical integration, which should based on 3x3x3 points. What the weight should be? The equation is from this paper (SIAM J. SCI. COMPUT. Vol. 20, No. 4, pp. 1165-1191) on page 1172 http://diyhpl.us/~bryan/papers2/frey...0algorithm.pdf |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,783
Rep Power: 71    |
Quote:
You can find the formula also in the Finite Volume chapter of the textbook Ferziger, Peric and Street |
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
||
|
|

|
|
|
|
|
#4 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
double post ...
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,783
Rep Power: 71    |
||
|
|

|
|
|
|
|
#6 |
|
New Member
Rodrigo
Join Date: Mar 2020
Posts: 9
Rep Power: 6  |
Thank you all!
The coefficients are different from the paper. Any reason for that? |
|
|
|

|
|
|
|
|
#7 |
|
New Member
Rodrigo
Join Date: Mar 2020
Posts: 9
Rep Power: 6  |
||
|
|

|
|
|
|
|
#8 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
Quote:
I think it's point two! |
||
|
|

|
||
|
|
|
#9 | |
|
New Member
Rodrigo
Join Date: Mar 2020
Posts: 9
Rep Power: 6  |
Quote:
You can check on page 1172: http://diyhpl.us/~bryan/papers2/frey...0algorithm.pdf |
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
Seems that the formula in the paper is wrong. Or they may use a generic weighting of the points.
Note that the only important fact is that the sum of all points contributing to integral must sum to unity. If the weights are different than the quadrature is defined according a different norm or point distribution. Regards |
|
|
|

|
|
|
|
|
#11 |
|
New Member
Rodrigo
Join Date: Mar 2020
Posts: 9
Rep Power: 6  |
||
|
|

|
|
|
|
|
#12 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
I have used my brain, starting from the one dimensional case. it's actually really simple.
You have to understand how the multi-D quadrature works on tensor-product elements. |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,783
Rep Power: 71    |
The general rule is to write the quadratic polinomial in x,y,z by factored 1D lagrangian interpolation, then the integral is analytic. You get the formula for the 3x3x3 stencil.
|
|
|
|

|
|
|
|
|
#14 |
|
Super Moderator
|
||
|
|

|
|
|
|
|
#15 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
||
|
|

|
|
|
|
|
#16 |
|
New Member
Rodrigo
Join Date: Mar 2020
Posts: 9
Rep Power: 6  |
||
|
|

|
|
|
|
|
#17 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
||
|
|

|
|
|
|
|
#18 |
|
New Member
Rodrigo
Join Date: Mar 2020
Posts: 9
Rep Power: 6  |
||
|
|

|
|
|
|
|
#19 |
|
Super Moderator
|
The formula in the paper is only exact for an affine function of the form
a + b x + c y So it is not based on Simpson. There are many possibilities and its not obvious what the authors have done. One suggestion: do a least squares fit of the nine values to the function a + b (x - x_i) + c (y - y_j) Then the integral is a * h^2 So what is a ? |
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
Yes I think we agree on that.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [snappyHexMesh] meshing of very small patches in comparison with the overall geometry | christos | OpenFOAM Meshing & Mesh Conversion | 3 | December 17, 2014 16:55 |
| [snappyHexMesh] Adding layers goes wrong with SnappyHexMesh | Elise | OpenFOAM Meshing & Mesh Conversion | 1 | April 22, 2013 02:32 |
| the initialization of the coupled level set method and vof model in FLUENT 13.0 | dutliang | FLUENT | 3 | December 13, 2011 21:28 |
| Problem on high density ratio in Level Set method | Kai Yan | Main CFD Forum | 10 | December 25, 2007 06:12 |
| [Gmsh] Gmsh and samplesurface | touf | OpenFOAM Meshing & Mesh Conversion | 2 | December 10, 2007 02:27 |