 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: May 2020
Posts: 1
Rep Power: 0  |
Hello,
So I've got this problem that I need to solve the governing equations (x,y momentum and continuity with pressure correction (SIMPLE)) over a computational plane. But, I dont know how will I procceed from the physical plane to the computational one. I've been trying to figure this out from John D. Anderson's book but I can't find the solution. The physical space is a duct with a 90degrees turn at some distance. I have the original grid with its nodes so I know the position of the nodes at the first place. The grid is compressed near the wall also. How could I transform it into a computational space with η, ξ ? How can I transform the governing equations correctly with η and ξ ? Thanks. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Dear mech_eng_gr,
are you familiar with the chain rule? Consider a field variable f as a function of 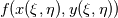 . Now you can start from the physical side . Now you can start from the physical side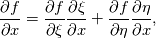 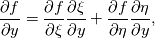 resulting in 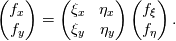 Or you start from the other side with 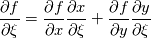 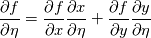 resulting in  Now since both sides must be identical it holds 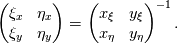 Here you may use the Cramer's rule for the right side. Now all you have to do is simply to replace your derivative expressions with the relations above before discretization. Moreover after that you also have to discretize the covariant metric terms 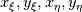 . .Regards Last edited by Eifoehn4; June 1, 2020 at 07:34. |
|
|
|

|
|
 |
| Tags |
| computational, grid, transformation |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| SU2-7.0.1 on ubuntu 18.04 | hyunko | SU2 Installation | 7 | March 16, 2020 04:37 |
| transformation code from gambit grid | dinhanh | Mesh Generation & Pre-Processing | 0 | June 5, 2017 09:34 |
| what is the computational formula of the grid spacings Δx+,Δy+,Δz+? | Detian Liu | Mesh Generation & Pre-Processing | 2 | April 26, 2013 11:48 |
| GRID TO GRID INTERPOLATION in FLUENT | calogero | FLUENT | 3 | June 4, 2003 08:32 |
| Non-uniform grid calculation | Aspens | Main CFD Forum | 1 | February 23, 2000 14:15 |