 |
|
|
[Sponsors] | |||||
LES box filter, filters big scales instead of small scales! |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Hello,
As you know, in LES, the filter function must filter(remove) the small scales and keep the large scales. But for the box filter in physical space(a), you can see that it keeps the values within range 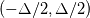 which means that small scales from which means that small scales from 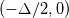 and and 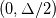 are kept and the scales bigger than are kept and the scales bigger than 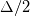 are set to zero. are set to zero. I think this is in conflict with its spectral definition! In spectral space(b), it keeps the small wave numbers (big scales) and removes the large wavenumbers (small scales). Can somebody explain this to me? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
You are confusing the concepts. In the physical space the filter function is represented and you have the convolution product with the variable to produce the filtered variable. The more delta is greater, the more the variable is filtered. The transfer function in spectral space will show the effects of the filter function along the wavenumbers. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
|
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
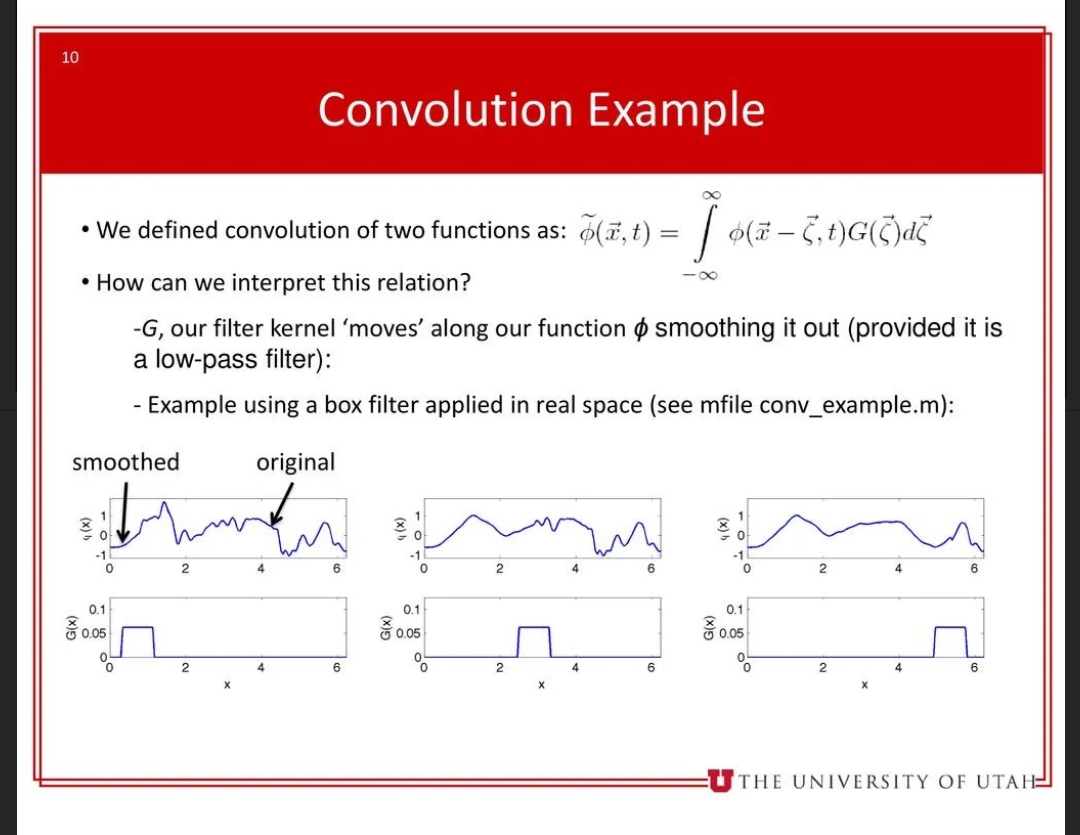
There are a lot of textbook you can use to see the filtering in physical space. It makes smoother the original function.
The concept is explained by the slide at page 8 in my lecture https://www.researchgate.net/publica...extFileContent |
|
|
|

|
|
 |
| Tags |
| les filter |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Y+ value for Large Eddy Simulation | yannossss | Main CFD Forum | 15 | March 21, 2017 23:41 |
| Dynamic Smagorinsky model- Filtering Concept | saeedi | Main CFD Forum | 34 | November 29, 2015 22:43 |
| Do small boats slow big boats? | Richard Scott | Main CFD Forum | 13 | August 3, 2004 03:51 |
| SGS small scales == fluctuant scales ?? | Bin Li | Main CFD Forum | 6 | February 26, 2004 12:35 |
| LES: Difference between physical space and fourier | K.Senthil Kumar | Main CFD Forum | 3 | July 3, 2000 08:36 |