 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Guest
Posts: n/a
|
Does anyone please tell me if inviscid flow can be rotational or not? What is the nature of rotational flow?
|
|

|
||
|
|
|
#2 |
|
Guest
Posts: n/a
|
Yes. Inviscid flow can be rotational. Rotational flow may be characterized by vorticity, which is the curl of velocity. A simple example is a vortex ring (like a cigarette smoke puff but without the diffusion process)
Check out fundamental fluid dynamic books. It is important NOT to confuse potential flow with inviscid flow (which may be the source of your confusion). While potential flow satisfies the equation of motion of inviscid flow dynamics, the reverse is not necessarily true. That is, an inviscid flow is not necessarily potential (the former may contain vorticity, which induces rotational and not potential flow) Adrin Gharakhani |
|

|
||
|
|
|
#3 |
|
Guest
Posts: n/a
|
Inviscid flow can be rotational. As pointed out in an earlier reply, inviscid flows with vortices are good examples.
It might help to know that vorticity is conserved in inviscid flows, i.e., Euler equations are incapable of vorticity production. So in an inviscid flow computation, vorticity (in the form of point vortices or vortex blobs or continuous fields) can only come in as a part of the inflow and can not be produced or destroyed by the Euler equations. Note also that the vortex rings can never be formed without viscosity though they can exist in a purely inviscid fluid. |
|

|
||
|
|
|
#4 |
|
Guest
Posts: n/a
|
> Euler equations are incapable of vorticity production. So in an inviscid flow computation, vorticity (in the form of point vortices or vortex blobs or continuous fields) can only come in as a part of the inflow and can not be produced or destroyed by the Euler equations.
This is true _only_ for the incompressible (and constant density) case. Example: baroclinic vorticity generation (without solid boundaries). Adrin Gharakhani |
|

|
||
|
|
|
#5 |
|
Guest
Posts: n/a
|
(1). It is not a good idea to mix these two terms at the same time. (2). At the begining, you have this equation called the Navier-Stokes equations, which represent the conservation of mass, momentum and energy. It contains viscosity terms. (3). Now, if you take the curl operation on the momentum equations, you will get this so-called "vorticity" equation. Remember that, the vorticity equation is derived from the momentum equation, so it has viscosity terms in it also. (4). If you set the viscosity terms to zero, you are going to get this mathematical equation, called "inviscid" equations, whether it is the inviscid momentum equations or the inviscid vorticity equation. (5). The inviscid momentum equation is generally called "Euler Equation" in contrast to the Navier-Stokes equations which has viscosity terms. (6). In the vorticity equation(derived from the Navier-Stokes equations), in addition to the viscosity terms, there are convection terms, stretching terms, production terms due to expansion, non-uniform density, and general body force. (7). So, even though you drop the viscosity terms, there are still many other terms in the vorticity equation, including the production terms. (8). So far, we have touched only the "inviscid" vs "viscous" forms of equation. (9). The rest of that is easy. The only time when the flow is "irrotational" is when the vorticity is everywhere zero. If there are still many terms in the vorticity equation (after dropping the viscosity terms), then you know that vorticity is normally non-zero. So, most of the time, it is rotational even without viscosity terms. (10). In old days, the inviscid equation was still very difficult to solve. So, the Euler equation was further simplified (second time) by setting the vorticity to zero (it is called "irrotational"). As a result, one can express the velocity in terms of the velocity potential and derive the so-called "potential flow"equation. (11). So, "potential flow" is "irrotational flow". And for the incompressible flow, the equation is the Laplace equation. The Laplace equation was the main focus in the 19th century. (12). Remember that, Euler equation and Laplace equation are simplified equations derived from the Navier-Stokes equations.(by setting the viscosity to zero, and then by setting the vorticity to zero, respectively)
|
|

|
||
|
|
|
#6 |
|
Guest
Posts: n/a
|
curved shocks can be a source of vorticity in an inviscid flow. i think there may be other potential sources but I can't remember what the others might be.
|
|

|
||
|
|
|
#7 |
|
Guest
Posts: n/a
|
where the velocity varies, where there exist vortex; where the entropy increases, where creates vortex.
|
|

|
||
|
|
|
#8 |
|
Senior Member
Nick
Join Date: Nov 2010
Posts: 126
Rep Power: 15  |
Many thanks guys you explained things that confused me for awhile. Especial thanks to Adrian, John and Kalyan
|
|
|
|

|
|
|
|
|
#9 |
|
New Member
Wencan Wu
Join Date: May 2018
Posts: 2
Rep Power: 0  |
I dont agree with you.
After a normal shock, velocity changes while no vortex exists. In laminar boundary layer, there entropy increases but no vortex generates. |
|
|
|

|
|
|
|
|
#10 |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
The vorticity equation derived from momentum equation for an inviscid incompressible flow is pressented below
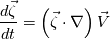 , where , where  I read in several textbooks that, from this equation we come to the conclusion that if 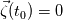 , then , then 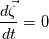 for for 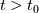 Also in many of theses textbooks is written that this equation agrees with Kelvin's circulation theorem, which states that, if an inviscid fluid is initially irrotational then it remains irrotational at all subsequent times. I can't understand, at least from a mathematical point of view, how that conclusion is made |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
||
|
|

|
|
|
|
|
#12 |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
||
|
|

|
|
|
|
|
#13 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Note that d/dt is the lagrangian derivative, formally that means the vorticity along the path-line.
|
|
|
|

|
|
|
|
|
#14 |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
||
|
|

|
|
|
|
|
#15 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
Setting x=0 does not automatically imply anything about dx/dt
For example, if x=1, it does not imply that d(1)/dt is anything Knowing f(a) doesn't tell you anything about f'(a) |
|
|
|

|
|
|
|
|
#16 | |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
Quote:
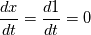 . The only thing I can think of is that if . The only thing I can think of is that if 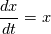 is an ordinary diff equation of position then x = 0 is a solution to this ode and so it satisfies the differential equation is an ordinary diff equation of position then x = 0 is a solution to this ode and so it satisfies the differential equation 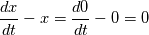 . .This type of solution means that if the system is at rest then it stays at rest. Can this be an analogy to the pde equation of vorticity? |
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
Join Date: Jul 2009
Posts: 357
Rep Power: 19  |
You have an initial value problem, with zero as the initial condition. The solution then is a constant, and that constant is the initial value zero. It really is that simple.
|
|
|
|

|
|
|
|
|
#18 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
You have to consider t=0, that is the equation writes dz/dt|t=0 = (z.grad v)|t=0 |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
When I say put vorticity=0 or x=1, I mean at one instance, not for all time.
For example, a new born child is born at a height (in US) of 20 inches. Eventually the baby grows into an adult and becomes much taller than 20 inches. d(baby height)/dt is not zero (for all time). Again.... f(a)=0 does not imply that f(t)=0 for all t. It simply means that f at t=a is 0. And it also does not imply anything about f'(t) = anything. So yes, you are missing something very obvious, again and again about general mathematical notation. Then you have the vorticity transport equation: 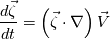 This equation is a general equation which relates the change of vorticity to velocity/vorticity field. Only from this equation can you evaluate what is 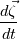 Without this equation, you know nothing about the change in vorticity. |
|
|
|

|
|
|
|
|
#20 |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
Quote:
Let me use some different notation just in case we implie the same thing but we "lost in translation" 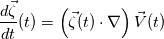 If we know that 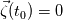 then, all I can say is then, all I can say is 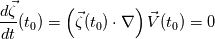 This is all I can understand. If you are telling me that there is something more than that, I'm sorry but maybe I need to go back to the basics, and the come back again to ask for help |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| interFoam inviscid and rotational | pablodecastillo | OpenFOAM Running, Solving & CFD | 7 | June 16, 2012 08:15 |
| Convergence for inviscid flow over sylinder | Rjakk | Main CFD Forum | 2 | March 21, 2007 10:53 |
| Inviscid flow | Atit Koonsrisuk | CFX | 12 | January 2, 2003 12:40 |
| Separation by Euler equations | Jitendra | Main CFD Forum | 9 | July 5, 2000 14:58 |