 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Sangho Ko
Join Date: Oct 2021
Location: South Korea
Posts: 136
Rep Power: 4  |
Hello everyone.
I'm reading paper and I don't understand some part. So I want to ask you. Link of this paper is below. https://www.researchgate.net/publica...bulence_Models I'm not good at English so there can be difficulty to communicate. Also cause of this, there is a confusion of nomenclature and it is hard to understand meaning of sentence from paper. So please understand me. In addition there are many questions. Cause of many questions, it can be annoying. Sorry. But I really need your help. Please understand me. Thanks  1. In page 1, "Finally, further from the impingement point the flow does revert to a thin shear flow but by no means to a simple one, with the maximum shear stress occurring outside the wall region and the flow thus retaining a significant memory of its upstream history. " * Actually I'm not sure that I understand the correct meaning of this sentence because my English is not good. But I've written qustions to extent that I understand. If I misundertand the meaning of sentence, let me know. A. Thin shear flow What is thin shear flow? B. Wall region What is wall region? I've uploaded figure that describe what I understand(wall jet region). C. Retaining a significant memory of its upstream history What does it mean? 2. In page 6, 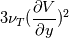 A. How it can be derived? I don't know how it is derived? 3. In page 6, "In a simple shear flow the action of 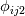 is to transfer a proportion of the energy generated in streamwise fluctuations to those in the plane orthogonal to the mean velocity" is to transfer a proportion of the energy generated in streamwise fluctuations to those in the plane orthogonal to the mean velocity"A. Transfer a proportion of the energy generated in streamwise fluctuations to those in the plane orthogonal to the mean velocity I don't undertstand this situation. 4. In page 6, "thus the intervention of 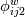 reduces the effective generation rate of reduces the effective generation rate of 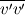 ." ." A. Reduction of generation rate of
4. In page 6, "Thus, in a stagnation flow the wall ‘damping’ term 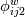 actually leads to an augmentation of the turbulent velocity normal to the wall. " actually leads to an augmentation of the turbulent velocity normal to the wall. "A. Damping term ' In question 2 and 3, we've seen 5. In page 6, We note, however, that if (as proposed in ref. [13]) the recorded mean velocity of the single hot wire on the axis is interpreted as 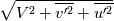 , Fig. 3, the predicted profile with Model 3 for H/D = 6 accords quite well with the experimental data with, in particular, the strongly non-linear variation very close to the wall being well captured. A. Mean velocity and fluctuation
6. In page 6, "Model 1 and, to a lesser extent, Model 2 produce too high near-wall velocities because the turbulence levels they predict are excessive." "Model 4 gives too low velocities because of the excessive mixing of the jet before coming under the influence of the wall." A. Excessive mixing In my opinion, I think I understand first sentence properly. 7. In page 8, "Models 3 and 4 achieve close correspondence with the measurements whereas Models 1 and 2 produce too rapid mixing as would be expected from the excessive predicted levels of shear stress shown in Fig. 6. " A. Damping function '
8. In page 9, "The reason for this apparent inconsistency is that, unlike the case of a thin shear layer, the normal stress terms make a substantial contribution to the mean momentum budget for r/D < 1.5" A. Normal stress term and Mean momentum What does it mean? Thanks for reading this long questions. I'm not good at English so please excuse my bad English. I'm not professional about turbulence. But I'm interested in that field. So help me please Thanks 
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
1A. Simple shear flows are your elementary flows like Couette flows and the the boundary layer that develops between parallel layers of fluid with different velocities. It is not the viscous sublayer. The point is, even though far from the point of stagnation, a wall boundary layer develops, thi wall boundary layer is still rather complex and not an elementary boundary layer that you find over a flat plate.
1B. The wall region of a jet impingement flow is the region away from the stagnation point where the wall boundary layer is developing and the flow is mostly parallel with the wall (instead of normal to the wall). There's a lot of pictures like so that demonstrate this. 1C. It means the correlation time and length scales are larger than in simple shear flows. The correlation is the information. 2A. The production term is the product of the Reynolds stress with the deformation. I forget how to derive exactly 3 but the square of the gradient should be there. The production is exact if you know the Reynolds stresses. Maybe the wiki gives you some hints. 3. What you have written down is the stress-strain correlation. The mechanism being discussed is the pressure-strain correlation. 4. This is again the influence of the pressure-strain and how it acts differently here compared to simple shear flows. 5. This requires a lesson in how hot-wires work and hot to correct them in practical scenarios. A single wire hotwire has a strong sensitivity flow perpendicular to its axis but it can't differentiate which velocity is which. In other words, single-wire HWA doesn't actually measure V even if you orient the hot-wire perfectly. (to be continued) |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
A further note on the damping term that I think will help you understand your remaining questions. The damping term in ordinary shear flows steals energy from streamwise fluctuations transfers them orthogonal to the flow direction. In other words, it mixes them out.
When turbulence encounters a wall, something entirely different happens. Due to the kinematic blocking effect of the wall (i.e. the flow encounters a wall) the wall-normal gradients are zero. Keep in mind that wall-normal is also streamwise with respect to the impinging jet (i.e. wall-normal and jet-axis are the same direction). The kinematic constraint is dV/dy and dv'/dy=0. This means that v' tends towards a maximum at the wall. This isn't merely a claim of the authors, it's basic physics guaranteed to occur (unless the fluid somehow teleports itself through the wall). The pressure-strain correlation is one of the mechanisms that allows this transfer of energy (augmenting the v') to take place. This phenomenon would actually correspond to a negative turbulence viscosity in ordinary mixing length models. In simple shear flows, the damping term steals energy from the v' fluctuations (and mixes them down); in the case of impinging jets it can do the opposite and amplify them, but it does so only near the stagnation region where the impinging effect occurs. 6. In simple shear layers, streamwise (i.e. wall parallel) fluctuations are larger than normal ones. For impinging jets, wall-normal fluctuations (which is streamwise-jet) can become large. Again, be very careful with the meaning of streamwise for a shear layer versus an impinging jet. In a wall-bounded shear layer, the wall is parallel with the mean flow. In an impinging jet, the wall is normal to the jet axis. |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Sangho Ko
Join Date: Oct 2021
Location: South Korea
Posts: 136
Rep Power: 4  |
Quote:
But apart from that, I don't understand why dV/dy and dv'/dy must be zero on the wall when jet impinges to the wall? I think if jet is shot to the wall, jet must approach stagnation point. Then mean normal velocity(V) becomes zero in stagnation point.(V=0) There is no flow rate that towards to wall. Flow never penetrates into the wall. So I think as jet approaches to the wall, mean velocity of jet(V) should be decreased. It means there is a Mean velocity gradient(dV/dy). But why dV/dy must be zero on the wall for jet impingement? And also why v' must be maximum on the wall? If dv'/dy must be zero on the wall, v' can be maximum or minimum. But how can we decide whether v' must be maximum or minimum? I've guessed it in terms of Boussinesq's hyptothesis to grasp approximate trend because I think both Boussinesq's hypothesis and Reynolds Stress model have similar concept although there can be difference of quantification. (Mixing: Boussinesq's hypothesis 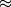 Reynolds Stress Model: "Damping term steals energy from streamwise fluctuations then transfers them orthogonal to the flow direction.") Reynolds Stress Model: "Damping term steals energy from streamwise fluctuations then transfers them orthogonal to the flow direction.")(Is upper convincing? I want to be confirmed whether I understand properly or not.) I think dV/dy becomes maximum on the wall when jet impinges to the wall.(as I've told you in upper) Because it approaches to the stagnation point, velocity of jet is decreased extreamly. Cause of this high fluctuation(v') occurs. But why dV/dy must be zero on the wall when jet impinges to the wall? Thanks 
|
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
The kinematic blocking condition, the boundary condition for a wall (regardless of slip or non-slip), is that the wall normal gradient is zero. Actually it's not just just V and v' but also U,W, u', and w'. Exactly on the wall the velocity is zero, but in a layer of fluid just above the wall, they approach maximums. This happens actually also for simple shear flows (k is maximum near the wall and 0 exactly on the wall). It may appear that there are two sets of conditions being applied in a small region (near the wall in this case) and that is true. The reconciliation of these two conditions is exactly what leads to boundary layers in physics. See figure 2. You can see that v' abruptly goes to zero in a very small region next to the wall.
You can't interpret maximum/minimum that way for vectors because the flow direction can be the opposite. Furthermore, the rms v' is the same whether positive or negative. Mixing means I take areas of stuff with high quantities and I send them to areas of with low quantities of stuff. I.e. i.e. if I put sugar in my coffee, I stir it to mix the areas with high sugar concentration with low sugar concentration to get an even drink. If the opposite happens (I stir my coffee and sugar cubes start forming), we don't call it mixing! Eddy viscosity models generally consider energy is transferred from regions of high to low strain and not the opposite. If you want to understand why v' is a maximum near the wall (but not on the wall) we can continue further but it has nothing to do with what turbulence model you are using. Last edited by LuckyTran; February 20, 2022 at 17:25. |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Sangho Ko
Join Date: Oct 2021
Location: South Korea
Posts: 136
Rep Power: 4  |
Quote:
 Actually what I want to know is not what model is most appropriate but why that physical situation happens. 1. I can see v' abruptly goes to zero from figure 2. But I don't understand how it is related to reason why dv'/dy=0 and v' becomes maximum near the wall. 2. I can understand the situation that "energy from streamwise fluctuations then transfers them orthogonal to the flow direction." But I want to know how it can be same context with "consider energy is transferred from regions of high to low strain and not the opposite" "streamwise fluctuations=High strain" : Actually I think it can be, cause of fluctuation. "orthogonal to the flow direction= Low strain": But I don't understand how this can be applied. Scenario that I've thought about upper is follow. Let's assume there is a flow on the flat plate like uploaded figure. From this figure we can see there is a velocity difference in x-direction between upper side and below side because of fluctuation(u') It means there is a high strain by velocity gradient(difference, du/dy). But there is No velocity difference in y-direction between left side and right side(blue colored line) It means there is no strain and velocity gradient(No dv/dx). So I guess 'transform of energy from high strain to low strain' means energy from streamwise fluctuation(High strain) is trasferred to orthogonal direction(Low strain). So energy(v') that is orthogonal to the flow direction occurs and it starts to mix. Is it right? Thanks 
Last edited by FluidKo; February 21, 2022 at 02:24. Reason: To add some coment |
||
|
|

|
||
 |
| Tags |
| jet impingement, turbulence |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Need help with arriving at the results of a journal paper | vivjk94 | Main CFD Forum | 6 | February 1, 2021 08:33 |
| The results of the viv numerical simulation do not match the results of the paper | zxh666hahah | OpenFOAM Verification & Validation | 0 | September 5, 2020 01:28 |
| Validating a paper on wing tip vortices | holy | FLUENT | 4 | May 3, 2012 06:20 |
| default values of kOmega (Wilcox) different from paper | romant | OpenFOAM Running, Solving & CFD | 2 | August 3, 2011 06:43 |
| Question about Hrv's Gamma diff scheme paper | santiagomarquezd | OpenFOAM Programming & Development | 1 | December 10, 2010 10:06 |