 |
|
|
[Sponsors] | |||||
Confusion in calculation of u', the velocity flucation |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
CPark
Join Date: Apr 2021
Location: Germany
Posts: 11
Rep Power: 5  |
Dear all,
I have a simple dataset with just the 3 components of velocity,  , ,  and and 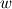 , and I am trying to compute the turbulence kinetic energy, , and I am trying to compute the turbulence kinetic energy, 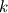 , in which the velocity fluctuations need to be computed. , in which the velocity fluctuations need to be computed.The velocity fluctuation 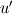 is simply, is simply, 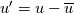 , where , where 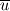 is the time average of is the time average of  . .The confusion is, say the dataset exists from time 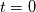 to to 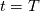 with a finite number time steps and i would like to compute with a finite number time steps and i would like to compute 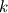 for each timestep. So for example for for each timestep. So for example for  where where 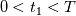 , I need to compute the , I need to compute the 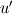 at this specific time. Then, is at this specific time. Then, is 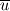 the time average between the time average between 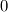 and and 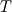 or is it between or is it between 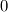 and and 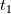 ? ?It is a simple base theory for CFD but I just ran into this confusion while trying to calculate 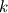 by myself instead of relying on programs. by myself instead of relying on programs.
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
You should average all times. There is only one average.
Technically the answer is neither. What you are looking for is the population quantity in statistics. What you can obtain is a sample estimate of the population quantity. The real time average is from time going from negative infinity to positive infinity. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
The time averaging must be theoretically extended up to T->Infinite. Therefore, in practice you have to compute from 0 to T, but T must be enough large. |
|
|
|

|
|
|
|
|
#4 | |
|
New Member
CPark
Join Date: Apr 2021
Location: Germany
Posts: 11
Rep Power: 5  |
Quote:
This leads me to another question. Since k is a time varying parameter and involves the mean of the squared u' (UPrime2mean as OpenFoam calls it), does it mean that this mean is not computed as poulation average but instead just the average up until the specific time t that I am computing k for? |
||
|
|

|
||
|
|
|
#5 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
|
||
|
|

|
||
|
|
|
#6 | |
|
New Member
CPark
Join Date: Apr 2021
Location: Germany
Posts: 11
Rep Power: 5  |
Quote:
So is the (u'u')_bar term a time varying parameter? |
||
|
|

|
||
|
|
|
#7 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
[f_fil(x,t)]_bar = F(x) |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
UMean and UPrime2Mean are averages from 0 to T and both of these are sample estimates for population statistics. There are infinite number of possible such estimators. You only really care about the best estimator that you get in the very last time dir because it is averaged over the longest time duration. Getting the population value is not possible unless you have the entire population ensemble, which means running your simulation until T=>infinity.
Hence, it's nearly impossible to directly calculate the time-varying u' and time-varying k at runtime because you don't know (and can never know) the population statistics. You must calculate it until T=>infinity, save U at all the times you care about, and then post-process it a posteriori. If you waned to do this manually you would run your simulation with fieldAverage option set. Go to the very last time dir and find UMean. Copy (and overwrite) this latest UMean into all previous time dirs. Then do something like: Code:
foamCalc addSubtract U subtract -field UMean -resultName UPrime And then calculate k. |
|
|
|

|
|
|
|
|
#9 | |
|
New Member
CPark
Join Date: Apr 2021
Location: Germany
Posts: 11
Rep Power: 5  |
Quote:
However, I am not sure how k can be time varying when it only depends on the 3 directional components of UPrime2Mean which are not time varying. What am I missing? |
||
|
|

|
||
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
|
||
|
|

|
||
|
|
|
#11 |
|
New Member
CPark
Join Date: Apr 2021
Location: Germany
Posts: 11
Rep Power: 5  |
I am currently considering LES for k, the resolved k to be precise.
Apologies, I did not really get what you meant by "[f_fil(x,t)]_bar = F(x)" but thanks for helping me recall that in LES it is a filtering operation instead of averaging. I completely missed that. Anyhow, according to Sagaut's book on LES for incompressible flow, the resolved turbulence kinetic energy is simply half of the squared of filtered velocity (page 51). Since the velocity data I have is for the given grid, the filtered velocity in my case is simply this velocity data. Does this sound like a valid statement? |
|
|
|

|
|
|
|
|
#12 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
Your LES database provided for sure the filtered velocity. From that you can deduce the k (unsteady) but also the approximation for the RANS (steady) velocity and the fluctuations. My previous notation means you can apply the time averaging to the filtered variable and the result is a steady field. |
||
|
|

|
||
|
|
|
#13 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
The instantaneous k depends on the three direction components of u', not uPrime2Mean. UPrime2Mean is the root mean square of u', it is a statistic like UMean. k inherits the temporal characteristics of u'.
You can get the time-averaged k from UPrime2Mean, but not the instantaneous k. 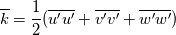 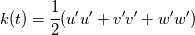 And 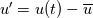 UPrime2Mean is 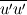 , ,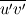 , ,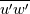 , ,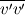 etc. etc.
|
|
|
|

|
|
|
|
|
#14 | |
|
New Member
CPark
Join Date: Apr 2021
Location: Germany
Posts: 11
Rep Power: 5  |
Quote:
Quote:
Thank you FMDenaro and LuckyTran for your kind replied. I have eventually figured it out with your help and managed to calculate the TKE of my dataset. |
||
|
|

|
||
 |
| Tags |
| turbulence kinetic energy, velocity component, velocity fluctuation |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Panel-Method, velocity calculation | mrbm | Main CFD Forum | 17 | August 5, 2022 11:03 |
| fluctuation component of velocity (Urms) calculation from RANS simulation results | atul1018 | Main CFD Forum | 5 | February 4, 2021 10:09 |
| Calculation of tangential velocity | lxlylzl.123 | FLUENT | 4 | November 18, 2020 14:13 |
| Time dependent angular velocity calculation UDF | shashankmechguy | Fluent UDF and Scheme Programming | 1 | July 26, 2018 02:23 |
| The problem for velocity calculation using turbulent model in openfoam. | mscheng | OpenFOAM Running, Solving & CFD | 6 | September 10, 2013 08:35 |