 |
|
|
[Sponsors] | |||||
On the discretization of cross-diffusion like terms in turbulence models |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
|
With a misuse of nomenclature, I define as "cross-diffusion" the terms of the following form:
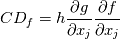 which appear in the RHS of a transport equation for the independent variable  and where and where  and and  are non constant and might themselves involve are non constant and might themselves involve 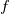 . .The two most known examples of these terms are for the Spalart-Allmaras model (where really the term "cross" is a misuse): 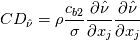 and the latest iterations of the Wilcox and Menter 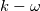 models, whose models, whose 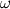 equations contain terms of the form: equations contain terms of the form: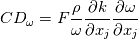 where F is non constant and also discontinuous. A common way to discretize 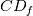 in the SA model is by exploiting the following equality: in the SA model is by exploiting the following equality: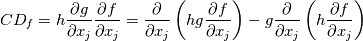 which allows an implicit treatment and enhances stability. However, the same is not formally valid for the 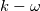 because of the discontinuity in because of the discontinuity in 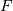 . Still, for shocks, even the SA rearrangement would be invalid, because of the discontinuity in . Still, for shocks, even the SA rearrangement would be invalid, because of the discontinuity in 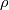 . .My question then is, have you ever tried this sort of discretization with some turbulence model different from the SA, despite it not being formally valid? Was it effective nonetheless in enhancing stability with only negligible differences in results? |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,275
Rep Power: 34   |
Quote:
I do this way in Wildkatze and it was observed to produce some instabilities so i under-relaxed this term a bit. However this is not the biggest source of instability in my opinion, still the term is nasty over-all. I should add that over-all implementation in Wildkatze is very stable but it is hard to pin point what exactly creates this stability. I implemented based on what i think would be stable method based on over all experiences with numerical method. So under-relaxing this term was not the only thing done. Better gradients i believe also plays a big role in all this. |
||
|
|

|
||
|
|
|
#3 | |
|
Senior Member
|
Quote:
And, while you need to use some underrelaxation factor specific to it, you have found that this way of implementing it is still superior to, say, the one suggested by Menter, where the whole 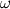 source term implicit part gets the following coefficient (where P, D and C stand for production, destruction and cross-diffusion)? source term implicit part gets the following coefficient (where P, D and C stand for production, destruction and cross-diffusion)?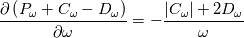 And finally, that you didn't find notable differences in the results with the two formulations? Thanks for the clarification |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,275
Rep Power: 34   |
I meant I use this one only. I directly compute it from the gradients coming from Turbulence Model.
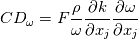 I use it in an explicit manner so no terms go to the Ap. Though now that you have put this thought into me, I MIGHT consider implicit formulation. I do under-relax it because it was found to be bit unstable. Nowadays the current implementation is very stable in Wildkatze. Perhaps the reason is that flow model is stable so may be turbulence model is adjusting to it. Usually turbulence models make flow unstable but since flow model is very robust it all seem to work out. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
|
Ok, I see, thanks.
Then I suggest you to try the Menter recipe. I never had any specific problem with it. My alternative formulation is kind of still a random idea at the moment, but it works great for SA. My concern is more around the resulting solution, because what I called F in the CD for k-w is something with a discontinuous derivative and I don't think that the rearrangement is valid there. But it would be even worst for SA with shocks, as the density itself is then discontinuous. I would have tried myself, but I'm currently validating a rewrite of the original formulation, so this can only happen somehow later. To be honest, there are also slight inconsistencies in the reformulation above when seen from a FV context. That is, you can't implement it correctly if you just volume integrate the two terms. You need to approach them from a point source perspective. |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,781
Rep Power: 71    |
Quote:
Paolo, just my curiosity, why do you talk of discontinuity, this is for the unresolved shock layer? Formally, in your viscous flow problem there is no singularity. And the action of the turbulence model should smooth the gradients. In conclusion, you could consider to limit the numerical oscillations around the spikes of the functions. |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
|
For SA it was my speculation, and while in practical terms I have a discontinuity, I see what you mean that I formally don't have one. Indeed, I never had any practical problem with the SA reformulation shown above, not even for "practical" discontinuities like shocks.
But as the discontinuity will practically be there for any practical resolution (I mean in case of shocks), the question arises about if the given reformulation will practically work as the original one. I wasn't the one that devised the reformulation for SA, so I never really cared about it. For the k-w case it is a different matter, it's really just the F definition that involves functions with a discontinuous derivative. Obviously, a much less severe case with respect to a shock, but it is also always there around the boundary layer. Finally, in both models, a FV implementation also needs the following approximation of the last term: 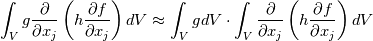
Last edited by sbaffini; January 31, 2023 at 06:40. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,781
Rep Power: 71    |
Have a look to the second mean value theorem, it could be useful for your FV implementation.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| 2D or 3D turbulence benchmark models | Deep111090 | Main CFD Forum | 2 | January 3, 2022 15:41 |
| Table bounds warnings at: END OF TIME STEP | CFXer | CFX | 4 | July 16, 2020 23:44 |
| variety of turbulence models in cfx? | hamidciv | CFX | 5 | January 4, 2016 02:41 |
| Turbulence intensity - cross wind on a body | Fabio88 | Main CFD Forum | 0 | May 4, 2015 03:44 |
| Why Turbulence models are not universal. | Senthil | Main CFD Forum | 4 | July 5, 2000 04:34 |