[Bottikowski96]

Hello together,

I am trying to simulate a turbulent channel flow without an inlet velocity. Therefore, I read some references and where it states that the simulations use forcing by a constant pressure gradient, represented by the forcing term f=(1,0,0) in the Navier-Stokes equation ([1], p. 3->screenshot is attached). What does this mean for the boundary conditions?

Thanks in advance

[1]: A. W. Vreman, J. G. M. Kuerten: 'Comparison of direct numerical simulation databases of turbulent channel flow at Reτ = 180'

[FMDenaro]

It means you have periodic BCs in streamwise and spanwise directions.

[Bottikowski96]

Thanks for you answer. But does it mean that I have to define a pressure value at the inlet and outlet to get a pressure gradient?

[FMDenaro]

Originally Posted by Bottikowski96

Thanks for you answer. But does it mean that I have to define a pressure value at the inlet and outlet to get a pressure gradient?

No, you have a constant pressure gradient term in the momentum equation plus a periodic fluctuation field you solve by means of the pressure equation with periodic BCs.

[Bottikowski96]

Okay, I got it. Thanks for your help!

[sbaffini]

Said otherwise, you need periodic boundary conditions and an x-momentum source term = 1, everything else is as usual

[Bottikowski96]

And what is the outcome of the periodic BCs in streamwise and spanwise directions? Are they used to saying the flow repeats in those directions?

[LuckyTran]

You have a plane channel, i.e. 2D, so you repeat the flow in spanwise direction.

You have a fully developed flow in the streamwise direction and that's why you use the periodic there. If this was instead a developing flow problem then you would specify the flow at the inlet (i.e. a velocity inlet) and likely you would not use the body force either.

You cannot force symmetry boundary conditions in spatially and temporally resolved simulations mirror-ing leads to very unnatural results. Instead you use natural conditions.

[Bottikowski96]

@sbaffini: So, I need periodic BC in streamwise and spanwise directions and no-slip conditions at the wall, right? What about the pressure, do I need a BC for it e.g. p=0 at the outlet? Moreover, I need to solve the incompressible NS-equations WITH a forcing term only in x-direction f=(1,0,0), right? And through the forcing term, the wall shear stress results in 1 which leads to a friction velocity of 1 (because the density is also 1)?

[LuckyTran]

The forcing term allows you to use periodic BCs on the remaining resulting pressure field. That's why you're doing it.

[sbaffini]

Originally Posted by Bottikowski96

@sbaffini: So, I need periodic BC in streamwise and spanwise directions and no-slip conditions at the wall, right? What about the pressure, do I need a BC for it e.g. p=0 at the outlet? Moreover, I need to solve the incompressible NS-equations WITH a forcing term only in x-direction f=(1,0,0), right? And through the forcing term, the wall shear stress results in 1 which leads to a friction velocity of 1 (because the density is also 1)?

As mentioned by LuckyTran, you need periodic bc's on pressure as well. All the other answers are YES

[Bottikowski96]

Thanks again for your answers, I really appreciate that! I really want to be sure that I have understood everything, so I have a further question regarding the BC. I would use the following BC for a 2D channel flow with height 'h' and length 'l':

no-slip BC : u=v=0 at y=0 and at y=h
periodic pressure BC: p(x=0) = p(x=l)

Would that be correct?

[sbaffini]

Originally Posted by Bottikowski96

Thanks again for your answers, I really appreciate that! I really want to be sure that I have understood everything, so I have a further question regarding the BC. I would use the following BC for a 2D channel flow with height 'h' and length 'l':

no-slip BC : u=v=0 at y=0 and at y=h
periodic pressure BC: p(x=0) = p(x=l)

Would that be correct?

Yes but, practically, it also depends from the specific scheme. The basic idea is to extend your scheme stencil at the boundaries using values from the other side

[Bottikowski96]

All right. Then, it would be possible to perform a simulation of a channel flow only with the no-slip conditions, because the forcing term causes the fluid to move?

[sbaffini]

Originally Posted by Bottikowski96

All right. Then, it would be possible to perform a simulation of a channel flow only with the no-slip conditions, because the forcing term causes the fluid to move?

Exactly. Once you look at the equations, your forcing term will be equivalent to an average pressure gradient, which will need an average wall shear stress to be balanced in the periodic setting. So, you'll get the average velocity profile that, according to your scheme, provides the average wall shear stress that balances the forcing term.

[Bottikowski96]

But why will be the forcing term equivalent to the pressure gradient term in the NS equations? In the case of a laminar, steady, incompressible channel flow, u (velocity in x direction) is unequal to zero and v (velocity in y direction) is equal to zero. Hence, the mass balance equation results in ∂u/∂x=0. Therefore, the y-momentum equation results in -(1/rho)*∂p/∂y=0 and the x-momentum equation in 0=-(1/rho) ∂p/∂x + nue*∂u∂u/∂y∂y + f_x, because all terms connected to v vanish as well as the gradients of u in x-direction.

[FMDenaro]

Originally Posted by Bottikowski96

But why will be the forcing term equivalent to the pressure gradient term in the NS equations? In the case of a laminar, steady, incompressible channel flow, u (velocity in x direction) is unequal to zero and v (velocity in y direction) is equal to zero. Hence, the mass balance equation results in ∂u/∂x=0. Therefore, the y-momentum equation results in -(1/rho)*∂p/∂y=0 and the x-momentum equation in 0=-(1/rho) ∂p/∂x + nue*∂u∂u/∂y∂y + f_x, because all terms connected to v vanish as well as the gradients of u in x-direction.

To understand the question, you should consider the non-dimensional form of the momentum equation using the u_tau velocity as reference. The pressure gradient requires a splitting to highlight the forcing term

You can read the details in Sec. 5.1 here (you can disregard the time-dependent forcing part):
https://www.researchgate.net/publica...ection_methods

[sbaffini]

Originally Posted by Bottikowski96

But why will be the forcing term equivalent to the pressure gradient term in the NS equations? In the case of a laminar, steady, incompressible channel flow, u (velocity in x direction) is unequal to zero and v (velocity in y direction) is equal to zero. Hence, the mass balance equation results in ∂u/∂x=0. Therefore, the y-momentum equation results in -(1/rho)*∂p/∂y=0 and the x-momentum equation in 0=-(1/rho) ∂p/∂x + nue*∂u∂u/∂y∂y + f_x, because all terms connected to v vanish as well as the gradients of u in x-direction.

Because:



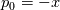so it implies the existence of a pressure that is linearly decreasing along x. Which is exactly what we know exists in such case.

In a sense, it's not different from when you solve for a gauge pressure, where the reference pressure disappears from momentum because it only is under gradient. Here, that linear part under gradient becomes a constant source and, by explicitly adding that source (and using periodicity for pressure) you are implicitly solving only for the pressure part on top of that linear variation.

[LuckyTran]

Note that you can definitely run a case with a specified pressure at the inlet and outlet. Your question was specifically about how the source term works.

Consider a pressure field such that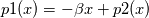

If p2 is periodic then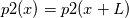

The pressure at any two stations separated by L is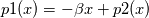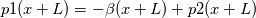


subtract one from the other and you get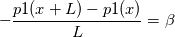



Beta is your forcing term and it is exactly equal to the pressure drop per period which is what you would have if you did a pressure inlet and outlet. Alternatively, if you take a normal navier-stokes solver, add a forcing term to it, it allows you to use periodic BCs on p2 (not the original p1 which is not periodic). Both approaches are equivalent. It's up to you which flavor you like.

[Bottikowski96]

Originally Posted by sbaffini

Exactly. Once you look at the equations, your forcing term will be equivalent to an average pressure gradient, which will need an average wall shear stress to be balanced in the periodic setting. So, you'll get the average velocity profile that, according to your scheme, provides the average wall shear stress that balances the forcing term.

Originally Posted by LuckyTran

Beta is your forcing term and it is exactly equal to the pressure drop per period which is what you would have if you did a pressure inlet and outlet. Alternatively, if you take a normal navier-stokes solver, add a forcing term to it, it allows you to use periodic BCs on p2 (not the original p1 which is not periodic). Both approaches are equivalent. It's up to you which flavor you like.

I have simulated a 2D laminar channel flow without a forcing term, with no-slip BC and ∂p/∂x=1 (in form of the BC: p(x=0)=length of channel | p(x=l)=0). This delivers the correct results. Then, I tried to run the same benchmark with no-slip BC again, but instead of the above pressure BC, I used a forcing term of f=(1,0). But then I get a velocity of zero in both directions in the entire domain. Why is that the case?