 |
|
|
[Sponsors] | |||||
NSEs with Incompressible Ideal gas as buoyancy term |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Nov 2023
Posts: 8
Rep Power: 2  |
Hi all,
I would like to know if the following formulation is correct. I am trying to express the NSEs in conservative form using the incompressible ideal gas model as the buoyancy term. Incompressible ideal gas assumes: 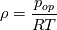 Where the density only varies with temperature and not pressure. The NSEs expressed in conservative form: 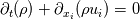 - Continuity - Continuity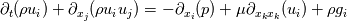 - Momentum - Momentum![c_{p}[ \partial_{t}(\rho T) + \partial_{x_{i}}(\rho u_{i} T)]= \kappa \partial_{x_{i}x_{i}}(T) + \dot{q} c_{p}[ \partial_{t}(\rho T) + \partial_{x_{i}}(\rho u_{i} T)]= \kappa \partial_{x_{i}x_{i}}(T) + \dot{q}](/Forums/vbLatex/img/e0e4c54dbf8bf2eb8667dc6c20351102-1.gif) - Energy - EnergyNote that the viscous dissipation and pressure work terms have been omitted from the energy equation. My question from here is, how do I proceed to solve this system of equations numerically? Given that I have expressed the density as a function of purely temperature, do I substitute it into my continuity, momentum, and energy equations? Or do I solve my system of equations separately from my equation of state, only updating the density field after marching forward in time. Any literature recommendations explaining the incompressible ideal gas model in detail, and especially its numerical implementation would be greatly appreciated. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
You certainly can substitute the equation of state directly and eliminate density if this is the only CFD you will ever do.
General purpose solvers will use various approaches because they want their code to solve many different types of problems, i.e. they want the same code to be easily switchable from incompressible idea gas to classical ideal gas with just the push of a button. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
Do you have some specific reason for that formulation? For small temperature variation, the Bousinnesq model works fine. Otherwise have a look to the low Mach formulations. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Join Date: Nov 2023
Posts: 8
Rep Power: 2  |
The code available to me uses the Boussinesq model, but the temperature range I encounter in my scenario is very large. From what I understand, Boussinesq assumes the density variation due to temperature is small, and thus approximately linear. This is not the case for me.
I chose to use the incompressible ideal gas model instead, as the pressure variation in my problem is very small. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
I am confused why you are asking how to numerically solve something if you already have a working code. What even is the question? I can't validate the performance of your code for you.
|
|
|
|

|
|
|
|
|
#6 | |
|
New Member
Join Date: Nov 2023
Posts: 8
Rep Power: 2  |
Quote:
Apart from the versatility of being able to switch between models, what are other benefits with applying the EOS separately from the NSEs? Is the implementation in the main solving loop more straightforward? Also, are there any additional modelling errors as opposed to substituting the EOS directly? Thanks, |
||
|
|

|
||
|
|
|
#7 | |
|
New Member
Join Date: Nov 2023
Posts: 8
Rep Power: 2  |
Quote:
The current code I have is purely incompressible, density is constant. I am not sure if I can include density as a field straight away, especially during the step which solves for pressure as a Poisson equation. I am still looking into this. |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
What you have is constrained coupled system of equations. You have your transport equations plus the EOS (the constraint).
When you hard-code the constraint into the transport equation you also force the errors/correctors to be forcibly propagated. When these correctors are large, they can cause the problem to diverge. A similar issue also occurs in the pressure-velocity coupling problem when you solve a Poisson problem for pressure. Not propagating them can mean you need more sweeps to converge (until the correctors are propagated throughout the domain). There is always a tradeoff between stability and convergence rate. Hence, there are endless permutations of solvers available. For example, sometimes you start cranking and end up with a negative temperature, now you have a negative density and you're screwed. |
|
|
|

|
|
|
|
|
#9 | |
|
New Member
Join Date: Nov 2023
Posts: 8
Rep Power: 2  |
Quote:
I will have to look further into this. Thanks for your advice |
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Starting from your code, it is suitable to use the low Mach formulation. That is largely used for combustion problems. This way you take into account larghe temperature gradient.
|
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 178
Rep Power: 4  |
Quote:
|
|
|
|

|
|
|
|
|
#12 |
|
New Member
Join Date: Nov 2023
Posts: 8
Rep Power: 2  |
Sorry I'm confused, why would the incompressible fluid be inviscid? And how exactly does this help?
|
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 178
Rep Power: 4  |
I never said anything about inviscid.
|
|
|
|

|
|
|
|
|
#14 | |
|
New Member
Join Date: Nov 2023
Posts: 8
Rep Power: 2  |
Quote:
My scenario is boundary layer flow over a flat surface, with temperature dependent heat release. I am not simulating combustion with species transport. |
||
|
|

|
||
|
|
|
#15 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 178
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#16 |
|
New Member
Join Date: Nov 2023
Posts: 8
Rep Power: 2  |
Correct. If I could, I would simply use the Boussinesq approximation with the incompressible NS, but my temperature range is very large. I can expect a deltaT of the order of 1000 K
|
|
|
|

|
|
 |
| Tags |
| buoyancy, convection, ideal gas, temperature and density |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| How does Fluent calculate the specific enthalpy for incomp. ideal gas? | brunolago | FLUENT | 0 | October 7, 2022 06:08 |
| Incompressible ideal gas | Nadaaaa22 | FLUENT | 5 | September 8, 2019 20:27 |
| Energy equation - Incompressible Ideal Gas? | Wingman | ANSYS | 3 | April 9, 2017 00:49 |
| difference between ideal gas and incompressible? | Ric | Main CFD Forum | 1 | March 24, 2007 12:07 |
| Gas pressure question | Dan Moskal | Main CFD Forum | 0 | October 24, 2002 22:02 |