 |
|
|
[Sponsors] | |||||
Maths problem when deriving conservation of energy equations. |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Abid
Join Date: Jun 2009
Posts: 4
Rep Power: 17  |
Hi,
Ive been reading John Andersons book 'Computational Fluid Dynamics the basics with applications'. Im upto the part where the energy equation is being derived. The energy equation is derived in nonconservation form and is in terms of the total energy e+ 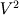 /2. This is on page 70. /2. This is on page 70. It then goes on to describe other ways that the equation can be written in different energy terms and begins to do some manipulations to rewrite the energy equations in terms of internal energy only. It starts by multiplying the momentum equations in nonconversation form by u, v, and w respectively. The original momentum equations are given below:  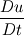 = - = -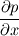 + +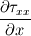 + +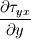 + +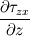 + + 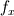 -- (2.50a) -- (2.50a) 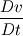 = - = -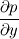 + +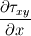 + + + +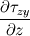 + + 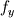 -- (2.50b) -- (2.50b) 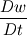 = - = -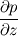 + + + +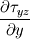 + +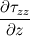 + + 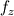 -- (2.50c) -- (2.50c)The first part of the manipulation involves multiplying the equations 2.50a, 2.50b, and 2.50c by u, v and w respectively. The book gives the results as shown below:  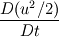 = - = -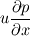 + +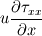 + +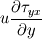 + +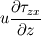 + + 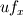 -- (2.67) -- (2.67)  = - = -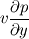 + +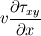 + +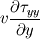 + +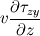 + + 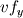 -- (2.68) -- (2.68) 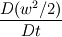 = - = -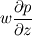 + +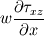 + + + +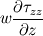 + + 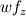 -- (2.69) -- (2.69)I can understand the right hand sides of the above three equations. But I dont understand how to get the left hand sides. I am confused how the following is equal:  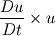 = =  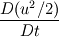 Can someone show me how this is done, and also tell me what area of differential mathematics I need to read to plug the gap in my knowledge. Thank you. |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Abid
Join Date: Jun 2009
Posts: 4
Rep Power: 17  |
||
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| turbulent energy spectrum problem | cfd.newbie | Main CFD Forum | 6 | September 24, 2015 16:13 |
| SIMPLE and energy equation convergence | Fabio | Main CFD Forum | 0 | June 1, 2007 06:06 |
| finite volume | daniel | Main CFD Forum | 17 | April 11, 2005 20:36 |
| Energy equation convergence problem | Reza | Main CFD Forum | 0 | August 27, 2003 13:09 |
| extremely simple problem... can you solve it properly? | Mikhail | Main CFD Forum | 40 | September 9, 1999 09:11 |