 |
|
|
[Sponsors] | |||||
[swak4Foam] Boundary condition set using groovyBC or codedFixedValue |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
behzad Ghasemi
Join Date: Sep 2013
Location: Iran
Posts: 56
Rep Power: 12  |
Hi dear foamers,
I want to solve 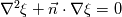 equation and obtain B (magnetic flux density) that is defined like equation and obtain B (magnetic flux density) that is defined like 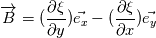 . actually the maxwell equations are rewritten based on vector potential . actually the maxwell equations are rewritten based on vector potential 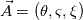 that in 2D becomes that in 2D becomes 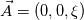 and and 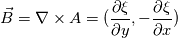 . my reference paper is "Level set method for two-phase incompressible flows under magnetic fields" http://www.sciencedirect.com/science...10465510000226 . . my reference paper is "Level set method for two-phase incompressible flows under magnetic fields" http://www.sciencedirect.com/science...10465510000226 .I've implemented the equation in my base solver. Now i want to test functionality of the new solver but i have some boundary condition problem before testing. For example if i want to get 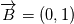 in boundaries i need to set in boundaries i need to set 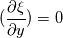 and and 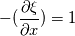 . is this condition my right boundary condition? correct me if I'm wrong. . is this condition my right boundary condition? correct me if I'm wrong.How can i implement this BCs? am i had to code new BC? Thanks in advance, Last edited by behzad-cfd; November 19, 2017 at 05:52. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
|
Dear Behzad,
it seems that fixedNormalSlip will fit your requirements: you will have tangential gradient component zero and the normal one equal to unity. Please check Doxygen for more description at https://cpp.openfoam.org/v5/classFoa...d.html#details An example: Code:
Wall
{
type fixedNormalSlip;
fixedValue uniform (0 -1 0);
}
__________________
Best regards, Dr. Alexander VAKHRUSHEV Christian Doppler Laboratory for "Metallurgical Applications of Magnetohydrodynamics" Simulation and Modelling of Metallurgical Processes Department of Metallurgy University of Leoben http://smmp.unileoben.ac.at |
|
|
|

|
|
|
|
|
#4 | |
|
Member
behzad Ghasemi
Join Date: Sep 2013
Location: Iran
Posts: 56
Rep Power: 12  |
Quote:
Thanks for your adequate reply. in your example I see fixedValue as vector but 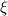 is a scalarField. I used this type and got error complaining that fixedNormalSlip is unknown. but when I use with same solver for vectorField like U it works. is a scalarField. I used this type and got error complaining that fixedNormalSlip is unknown. but when I use with same solver for vectorField like U it works.Any suggestion? |
||
|
|

|
||
|
|
|
#5 | |
|
Senior Member
|
Ohhh, sorry for misleading you. Fixed Normal Slip is something different.
Will reply you when I get the correct one. In this example you can only limit your tangential gradient of Psi to zero, the normal option gives you a value, not a gradient! Quote:
__________________
Best regards, Dr. Alexander VAKHRUSHEV Christian Doppler Laboratory for "Metallurgical Applications of Magnetohydrodynamics" Simulation and Modelling of Metallurgical Processes Department of Metallurgy University of Leoben http://smmp.unileoben.ac.at |
||
|
|

|
||
|
|
|
#6 |
|
Member
behzad Ghasemi
Join Date: Sep 2013
Location: Iran
Posts: 56
Rep Power: 12  |
It's okay. I appreciate your effort to help me. waiting for your guidances dear Alexander.
Kind regards |
|
|
|

|
|
|
|
|
#7 |
|
Member
Nicolas Lussier Clément
Join Date: Apr 2009
Location: Montréal, Qc, Canada
Posts: 61
Rep Power: 17  |
Hi behzad-cfd,
I would you to clarify, the 3D equation you want to solve. Is it: 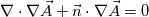 Then deduce 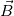 field from field from 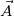 using using So to solve finite volume vector field the field 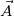 you need boundary condition on it. you need boundary condition on it. Your boundary condition should be set on the tensor 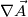 at the boundary, guessing with the value on at the boundary, guessing with the value on 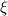 you gave: you gave: ![\nabla \vec{A}|_{\partial\Omega} =
\left[ {\begin{array}{ccc} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{array} } \right] \nabla \vec{A}|_{\partial\Omega} =
\left[ {\begin{array}{ccc} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{array} } \right]](/Forums/vbLatex/img/9dab0148f3b1512f06b1e1326fc57fde-1.gif) ??? I'm I correct ? Sadly i don't have access to the paper you mentioned to verify for my self. It seam mote like you wish So in the case you did the hole work of using 3D quantity 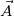 you have to fix you have to fix 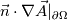 at the boundary. at the boundary. 2D Now If my assumption are correct and if you are only interested in the component 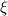 of field of field 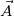 this is a fix gradient boundary condition on this is a fix gradient boundary condition on 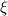 where where ![\nabla\xi = [-1,0,0] \nabla\xi = [-1,0,0]](/Forums/vbLatex/img/685e92a9bc446c4a413702c0c557e3aa-1.gif) at the BC provided you did not implemented at the BC provided you did not implemented 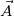 but the scalar field but the scalar field 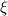 to solve only the "2D magnetic equation". Then to solve only the "2D magnetic equation". Then 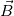 is a 3D vector with component "z" always equal to zero. But is a 3D vector with component "z" always equal to zero. But 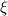 is a scalar and the boundary condition you set is is a scalar and the boundary condition you set is 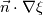 I hope this help. But I'm not quit certain to understand your question properly. I would need more clarification on the boundary you wish to set and access to the article in order to be of more help. Last edited by nlc; November 20, 2017 at 16:08. |
|
|
|

|
|
|
|
|
#8 |
|
Member
behzad Ghasemi
Join Date: Sep 2013
Location: Iran
Posts: 56
Rep Power: 12  |
Quote:
It appears that i couldn't explain the problem well. I took some screen shots from equations section of paper. maybe it'll help to clarify the problem. the last picture is magnetic field lines. I would like to get uniform magnetic filed like that. Regards, Behzad |
|
|
|

|
|
|
|
|
#9 | |
|
Member
Nicolas Lussier Clément
Join Date: Apr 2009
Location: Montréal, Qc, Canada
Posts: 61
Rep Power: 17  |
Quote:
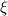 scalar field. If you want to set scalar field. If you want to set 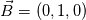 you do like you like written you do like you like written 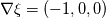 . Meaning you use gradient boundary condition on your scalar field with the value . Meaning you use gradient boundary condition on your scalar field with the value 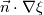 that you can calculate yourself. that you can calculate yourself. One thing that can cause problem with this way of doing is that there is no reference value for 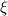 so this make the simulation less stable and can cause difficulty. In this regard you can set one of the BC (that is suppose to be homogeneous) to fix value 0 (in this case left or right). so this make the simulation less stable and can cause difficulty. In this regard you can set one of the BC (that is suppose to be homogeneous) to fix value 0 (in this case left or right).
Last edited by nlc; November 20, 2017 at 18:18. |
||
|
|

|
||
|
|
|
#10 |
|
Member
behzad Ghasemi
Join Date: Sep 2013
Location: Iran
Posts: 56
Rep Power: 12  |
Quote:
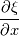 on paper? and then set the values on boundary patch? on paper? and then set the values on boundary patch?As far as i know there is not any boundary condition to calculate scalar gradient in vector form and give the tangential part. All of gradient BCs calculate patch normal gradient. am i correct? |
|
|
|

|
|
|
|
|
#11 |
|
Member
Nicolas Lussier Clément
Join Date: Apr 2009
Location: Montréal, Qc, Canada
Posts: 61
Rep Power: 17  |
Take a look at the tutorial:
surfaceTracking/bubbleInterTrackFoam/bubble2D_r0.75mm/ Code:
0/U:38: gradient uniform (0 0 0); 0/p:31: gradient uniform 0; So for U (velocity) it is 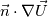 which is a vector !! which is a vector !!And for p (pressure) it is 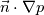 which is a scalar !! which is a scalar !!Mosley meaning that you can setup the entry BC for 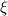 Code:
gradient uniform -1; Code:
fixedValue;
uniform 0;
Code:
gradient uniform 0; 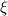 !! (Just in case you do some special stuff) !! (Just in case you do some special stuff) Hope this is clear now. You'd be kind to provide a picture of the result. Now if you want to create your own BC and use 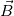 to setup to setup 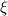 you can. Use the mathematical relation we discussed to set up the correct BC. But if I'd be you I'd do it in 3D from the start and apply it to you can. Use the mathematical relation we discussed to set up the correct BC. But if I'd be you I'd do it in 3D from the start and apply it to 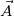 once you write the 3D version of the solver. (Just an opinion) once you write the 3D version of the solver. (Just an opinion)
|
|
|
|

|
|
|
|
|
#12 |
|
Member
behzad Ghasemi
Join Date: Sep 2013
Location: Iran
Posts: 56
Rep Power: 12  |
Quote:
I know what do you mean. but 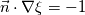 won't give us won't give us 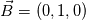 . Let us test this condition for bottom boundary where we want to impose B = (0, 1, 0): . Let us test this condition for bottom boundary where we want to impose B = (0, 1, 0):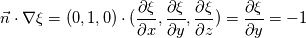 (1) (1)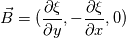 (2) (2)(1),(2)----> 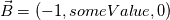 For this reason I believe we should have tangential gradient value = -1 to get desired B field. |
|
|
|

|
|
|
|
|
#13 |
|
Member
Nicolas Lussier Clément
Join Date: Apr 2009
Location: Montréal, Qc, Canada
Posts: 61
Rep Power: 17  |
No wrong boundary. You can send me your case if you want... Just think of the distribution (or the map) you want on
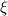 to have to have 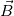 . There is a 90 degree rotation between . There is a 90 degree rotation between 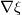 and and 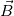 . You want . You want 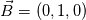 you do this with 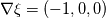 So BC are : On 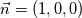 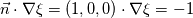 On 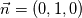 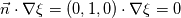 I'm not sure I understand your confusion. Do you wish to use 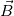 ?? ?? If you really want to use  to set up to set up  you would have to solve you would have to solve  for for 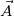 For the time being you can simply think of the map 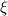 you need to have the value you need to have the value 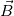 you want. you want. With the BC I suggest, you have what you want. If you think about it on 2 side of the box you have a normal gradient and on the other 2 boundary you have a variation tangent to the boundary !!! Like you wish just not by imposing it on the same boundary ! You could setup a "tangent" BC by fixing value on the boundary by building your own BC. But this seam to me like looking for trouble. If you really want to do this I suggest you start testing and compiling your BC before asking how to do it. You can find tutorial and documentation ... Last edited by nlc; November 20, 2017 at 23:48. |
|
|
|

|
|
|
|
|
#14 |
|
Member
behzad Ghasemi
Join Date: Sep 2013
Location: Iran
Posts: 56
Rep Power: 12  |
Quote:
Best regards |
|
|
|

|
|
|
|
|
#15 |
|
Member
Nicolas Lussier Clément
Join Date: Apr 2009
Location: Montréal, Qc, Canada
Posts: 61
Rep Power: 17  |
||
|
|

|
|
|
|
|
#16 |
|
Member
behzad Ghasemi
Join Date: Sep 2013
Location: Iran
Posts: 56
Rep Power: 12  |
Hi Nicolas,
Sorry about the delay. I had some issues with my solver. I was about to send the results. BTW here you are. First picture: ksi boundary condition: Code:
bottom
{
type fixedValue;
value uniform 0;
}
outlet
{
type fixedValue;
value uniform 0;
}
rightWall
{
type fixedGradient;
gradient uniform -1;
}
leftWall
{
type fixedGradient;
gradient uniform -1;
}
defaultFaces
{
type empty;
}
Code:
bottom
{
type fixedValue;
value uniform 0;
}
outlet
{
type fixedValue;
value uniform 0;
}
rightWall
{
type zeroGradient;
}
leftWall
{
type fixedGradient;
gradient uniform -1;
}
defaultFaces
{
type empty;
}
Code:
bottom
{
type fixedGradient;
gradient uniform -1;
}
outlet
{
type zeroGradient;
}
rightWall
{
type fixedValue;
value uniform 0;
}
leftWall
{
type fixedValue;
value uniform 0;
}
defaultFaces
{
type empty;
}
If i finished I'll report the results here. Kind Regards, Behzad |
|
|
|

|
|
|
|
|
#17 |
|
Member
Nicolas Lussier Clément
Join Date: Apr 2009
Location: Montréal, Qc, Canada
Posts: 61
Rep Power: 17  |
Try this and show me the result please. Has this is the boundary condition I was trying to describe to you. Obviously it seam I was not clear enough. This boundary condition will give you a
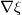 uniform of magnitude 1 and directed towards the outlet. Understanding that outlet is the top boundary condition. Finally according to your equation it should give you an horizontal magnetic field. If you do not get it there is something wrong uniform of magnitude 1 and directed towards the outlet. Understanding that outlet is the top boundary condition. Finally according to your equation it should give you an horizontal magnetic field. If you do not get it there is something wrong Code:
bottom
{
type fixedValue;
value uniform 0;
}
outlet
{
type fixedGradient;
gradient uniform -1;
}
rightWall
{
type zeroGradient;
}
leftWall
{
type zeroGradient;
}
defaultFaces
{
type empty;
}
Code:
bottom
{
type fixedValue;
value uniform 0;
}
outlet
{
type fixedValue;
gradient uniform -1;
}
rightWall
{
type zeroGradient;
}
leftWall
{
type zeroGradient;
}
defaultFaces
{
type empty;
}
As an end remark your result seam to be coherent with the 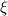 profile. If you plot the value of profile. If you plot the value of 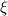 field and think of the implication of the equation you describe you'll understand what I mean. field and think of the implication of the equation you describe you'll understand what I mean. Regards |
|
|
|

|
|
|
|
|
#18 |
|
Member
behzad Ghasemi
Join Date: Sep 2013
Location: Iran
Posts: 56
Rep Power: 12  |
Quote:
The problem solved and i got the uniform magnetic field by setting side walls as fixedGradient and top and bottom zeroGradiendt. As you mentioned there is a 90 degree transformation in equations and i should have rotated BCs 90 degree to achieve desired field. Kind regards, Behzad |
|
|
|

|
|
 |
| Tags |
| bondary conditions, codedfixedvalue, groovybc |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Ansys Licence Serve on Ubuntu 16.04 LTS | david.pasquale | ANSYS | 2 | January 20, 2017 11:52 |
| several fields modified by single boundary condition | schröder | OpenFOAM Programming & Development | 3 | April 21, 2015 05:09 |
| Low Mixing time Problem | Mavier | CFX | 5 | April 29, 2013 00:00 |
| External Radiation Boundary Condition (Two sided wall), Grid Interface | CFD XUE | FLUENT | 0 | July 8, 2010 06:49 |
| Convective Heat Transfer - Heat Exchanger | Mark | CFX | 6 | November 15, 2004 15:55 |