 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Tom
Join Date: Apr 2017
Posts: 50
Rep Power: 9  |
Hi All,
I have a very fine mesh of a turbomachinery component. The value of y+ is smaller than 1. I want to run simpleFoam with the flow being fully resolved near the walls. My understanding is that the parameters which need to be modified are k, omega and nut. My question is what should they be set to? is it zeroGradient for all the walls. I'm running OpenFOAM v1906 Currently i have them like this: FoamFile { version 2.0; format ascii; class volScalarField; location "0"; object k; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -2 0 0 0 0]; internalField uniform 7.18; boundaryField { INLET-001 { type turbulentIntensityKineticEnergyInlet; intensity 0.0435; value $internalField; } EXIT-001 { type inletOutlet; inletValue uniform 7.18; value $internalField; } MERGEOGV-001 { type kqRWallFunction; value $internalField; } MERGEHUB-001 { type kqRWallFunction; value $internalField; } MERGECAS-001 { type kqRWallFunction; value $internalField; } FoamFile { version 2.0; format ascii; class volScalarField; location "0"; object omega; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 0 -1 0 0 0 0]; internalField uniform 4502; boundaryField { INLET-001 { type inletOutlet; inletValue uniform 4502; value $internalField; } EXIT-001 { type inletOutlet; inletValue uniform 4502; value $internalField; } MERGEOGV-001 { type omegaWallFunction; value $internalField; } MERGEHUB-001 { type omegaWallFunction; value $internalField; } MERGECAS-001 { type omegaWallFunction; value $internalField; } FoamFile { version 2.0; format ascii; class volScalarField; location "0"; object nut; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // dimensions [0 2 -1 0 0 0 0]; internalField uniform 0; boundaryField { INLET-001 { type calculated; value uniform 0; } EXIT-001 { type calculated; value uniform 0; } MERGEOGV-001 { type nutkWallFunction; value uniform 0; } MERGEHUB-001 { type nutkWallFunction; value uniform 0; } MERGECAS-001 { type nutkWallFunction; value uniform 0; } |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Andrea
Join Date: Feb 2012
Location: Leeds, UK
Posts: 179
Rep Power: 16  |
Hi Tom,
in my experience with wall-resolved meshes and low-Re models, if your mesh satisfies  everywhere at the wall using either kqRwallFunction or fixedValue and a value ~0 for k does not make any significant difference. Either way, I would use a value close to zero since, strictly speaking everywhere at the wall using either kqRwallFunction or fixedValue and a value ~0 for k does not make any significant difference. Either way, I would use a value close to zero since, strictly speaking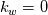 is the mathematically correct BC, so it does not make sense to use the free-stream value for k at the boundaries. The same holds for other turbulent variables such as omega and epsilon. My experience is mostly based on using the k-espilon Launder and Sharma low-Re model. For epsilon, the BC at the wall is 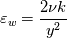 and because 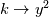 at the wall, it follows that epsilon has a finite value. Nevertheless, for practical purposes, I have found that both fixedValue and epsilonWallFunction with value ~0 are valid approximations which lead to good results with the Launder and Sharma low-Re k-epsilon. at the wall, it follows that epsilon has a finite value. Nevertheless, for practical purposes, I have found that both fixedValue and epsilonWallFunction with value ~0 are valid approximations which lead to good results with the Launder and Sharma low-Re k-epsilon.My experience with omega-based models on wall-resolved meshes is somehow more limited. However, theoretically 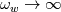 so you can get away with using either a fixedValue or omegaWallFunction with a high value for omega at the wall. A more precise estimation of this "high" value can be obtained by considering that the asymptotic behaviour at the wall is so you can get away with using either a fixedValue or omegaWallFunction with a high value for omega at the wall. A more precise estimation of this "high" value can be obtained by considering that the asymptotic behaviour at the wall is 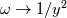 . The wall value for omega is then . The wall value for omega is then 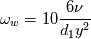 To sum it up, for "proper" wall-resolved meshes and low-Re turbulence models the influence of wall functions is somehow limited in my experience. A mathematically sound fixedValue for the turbulence variables at the wall should be enough (I have tested this in several cases with the Launder and Sharma k-epsilon, my experience with omega-based models is somehow more limited). In any case, sound values for the turbulence variables at the wall should be used with both fixedValue and wall functions BC types - using free stream values is conceptually wrong and can lead to numerical issues as well. Hope this helps, Andrea Last edited by Andrea1984; February 20, 2020 at 06:31. |
|
|
|

|
|
|
|
|
#3 | |
|
Member
Tom
Join Date: Apr 2017
Posts: 50
Rep Power: 9  |
Quote:
Hi Andrea, Many thanks for your detailed answer. What about setting all the walls to zeroGradient, would this not switch off the wall function? Best Regards, Tom |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Andrea
Join Date: Feb 2012
Location: Leeds, UK
Posts: 179
Rep Power: 16  |
Hi Tom,
that would deactivate the wall-functions indeed, but from my previous post I would say that a Dirichlet (fixedValue) wall BC is more physically and mathematically sound for turbulence variables than a Neumann (zeroGradient). As far as I am aware, there is nothing in the equations for k, epsilon or omega that justifies a zeroGradient condition at the walls. Andrea |
|
|
|

|
|
|
|
|
#5 | |
|
Member
Tom
Join Date: Apr 2017
Posts: 50
Rep Power: 9  |
Quote:
Having had a more through search on the internet seems that the value 1.0e-11 is often suggested for k at wall when trying to resolve the viscous sublayer. In the last equation you quoted what is the 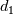 parameter? parameter?Also what do you set nut at the wall to? Tom |
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
Andrea
Join Date: Feb 2012
Location: Leeds, UK
Posts: 179
Rep Power: 16  |
Yes 10e-11 is a numerical way of saying zero, because that is the proper BC for k at the wall
 d1 is a model constant for k-omega SST (or maybe is beta1? sorry I can't remember). Its value should be 0.075. For nut, from the discussion above, I would say either a lowRe wall function or a fixedValue ~0. Andrea |
|
|
|

|
|
|
|
|
#7 | |||||
|
Member
Tom
Join Date: Apr 2017
Posts: 50
Rep Power: 9  |
Update:
I have tried applying fixedValue 1.0e-11 for k fixedValue 8.33e9 for omega and fixedValue 1.0e-11 for nut Using first order upwind schemes for U, k, omega i managed to get a residual drop of over 8 levels. Quote:
Quote:
Quote:
It seems now that the residuals start quite high Quote:
It also seems that after a few iterations the time step continuity error changes in the other direction: Quote:
After this, my simulation crashes. any idea what's going on? |
||||||
|
|

|
||||||
|
|
|
#8 |
|
Senior Member
Andrea
Join Date: Feb 2012
Location: Leeds, UK
Posts: 179
Rep Power: 16  |
Sorry Tom I can't see any straightforwad issue with your settings at a first glance.
Andrea |
|
|
|

|
|
 |
| Tags |
| fully resolved, komega sst model, simplefoam, yplus |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Airfoil with simpleFoam and kOmegaSST: high drag values? | Tsiolkovsky | OpenFOAM Running, Solving & CFD | 6 | November 21, 2018 05:56 |
| simpleFoam: switching flow direction with kOmegaSST RAS Model | JasonG | OpenFOAM Running, Solving & CFD | 1 | September 25, 2014 07:26 |
| simpleFoam with kOmegaSST | ilpaso | OpenFOAM Running, Solving & CFD | 11 | April 7, 2014 06:12 |
| fully developed channel with cyclic using simplefoam | ArathoN | OpenFOAM Running, Solving & CFD | 4 | February 21, 2014 09:53 |
| simpleFoam kOmegaSST LowRe pressure divergence | Pat84 | OpenFOAM Running, Solving & CFD | 2 | August 12, 2013 17:42 |