[Jerryfan]

Dear Foamers,


This question has been raised for several times at least here in this Forum. It seems that they all didn't give a clear answer. That's why I am trying to bring it up again.

http://www.cfd-online.com/Forums/ope...lculation.html

http://www.cfd-online.com/Forums/ope...ddtscheme.html (The #7)


http://www.cfd-online.com/Forums/ope...-operator.html

The calculation of the diagonal coefficients lots of times are done by the negSumDiag() function. The code is like this:

void Foam::lduMatrix::negSumDiag()
{
    const scalarField& Lower = const_cast<const lduMatrix&>(*this).lower();
    const scalarField& Upper = const_cast<const lduMatrix&>(*this).upper();
    scalarField& Diag = diag();

    const labelUList& l = lduAddr().lowerAddr();
    const labelUList& u = lduAddr().upperAddr();

    for (register label face=0; face<l.size(); face++)
    {
        Diag[l[face]] -= Lower[face];
        Diag[u[face]] -= Upper[face];
    }
}

The thing that confuses me here is, should it be like this: ?

for (register label face=0; face<l.size(); face++)
    {
        Diag[l[face]] -= Upper[face];
        Diag[u[face]] -= Lower[face];
    }

In santiagomarquezd's post, a 2D mesh was proposed: (Details were given in his post)

*-------*-------*-------*-------*
| 0 | 1 | 2 | 3 |
*-------*-------*-------*-------*
| 4 | 5 | 6 | 7 |
*-------*-------*-------*-------*

The calculation of diagonal coefficient for cell #1 is given in loops 0, 2 and 3 in the negSumDiag() function.

Loop #0:
Diag[u[0]] -= Upper[0]; (Equivalent to: Diag[1] -=Upper[0] )

Loop #2:
Diag[l[2]] -= Lower[2]; (Equivalent to: Diag[1] -=Lower[2] )

Loop #3:
Diag[l[3]] -= Lower[3]; (Equivalent to: Diag[1] -=Lower[3] )

In total,
Diag[1] = -(Upper[0] + Lower[2] + Lower[3])

This confuses me so much as it is very obvious that Diag[1] should be calculated as:
Diag[1] = -(Lower[0] + Upper[2] + Upper[3])

It might work for a symmetric matrix, but I really doubt about the non-symmetric case.
(correct me if I am wrong.)

The other thing that makes me even more confusing is the lduMatrix::H function.
The code:

template<class Type>
Foam::tmp<Foam::Field<Type> > Foam::lduMatrix::H(const Field<Type>& psi) const
{
    tmp<Field<Type> > tHpsi
    (
        new Field<Type>(lduAddr().size(), pTraits<Type>::zero)
    );

    if (lowerPtr_ || upperPtr_)
    {
        Field<Type> & Hpsi = tHpsi();

        Type* __restrict__ HpsiPtr = Hpsi.begin();

        const Type* __restrict__ psiPtr = psi.begin();

        const label* __restrict__ uPtr = lduAddr().upperAddr().begin();
        const label* __restrict__ lPtr = lduAddr().lowerAddr().begin();

        const scalar* __restrict__ lowerPtr = lower().begin();
        const scalar* __restrict__ upperPtr = upper().begin();

        register const label nFaces = upper().size();

        for (register label face=0; face<nFaces; face++)
        {
            HpsiPtr[uPtr[face]] -= lowerPtr[face]*psiPtr[lPtr[face]];
            HpsiPtr[lPtr[face]] -= upperPtr[face]*psiPtr[uPtr[face]];
        }
    }

    return tHpsi;
}

The part marked bold above means: (forget about the negtive sign in the code above and the source term below)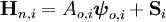



we see that it's not using:

for (register label face=0; face<nFaces; face++)
        {
            HpsiPtr[lPtr[face]] -= lowerPtr[face]*psiPtr[lPtr[face]];
            HpsiPtr[uPtr[face]] -= upperPtr[face]*psiPtr[uPtr[face]];
        }
    }

It's very strange. It seems the code contradicts itself in different usages.
Or there is some tricky part I didn't catch that makes these happen naturally.

Discussions on this are really needed.

[Tobi]

Dear Jerry,

first, good starting thread with all information and you took your time to prepare you question. I highly appreciate it. As you wrote me a private message, I will try to give you an answer based on the code that I see because I was not dealing with that classes till now. But first of all. If you think that the calculation is wrong, then all the validation cases that were calculated with openfoam should be wrong - luckily it is not like that. Okay lets start. You are asking about the behavior of the code of the negSumDiag() function. Can you please check you post because the code you posted and the code that is already implemented are identical. The second question belongs to the 2D case. Please check what you wrote again because the correction you mentioned is again similar to the one you mentioned above. Maybe you meant that one:

This confuses me so much as it is very obvious that Diag[1] should be calculated as:
Diag[1] = -(Lower[0] + Upper[2] + Upper[3])

Shouldn't it be like:

Diag[1] = -(Lower[0] + Upper[2] + Upper[5])

In that case I think I can give you the answer. The code is not taking the face ID as you see above with the begin() function and the fact that lowerPtr is a pointer pointing to a allocated memory that stores a scalar. After that, the loop starts and what you do here is finally to move the pointer lowerPtr forward with n bits. As the faces are stored within a list, they are stored in one line within the memory. You can imagine that as follow:

face of Cell 1 has the faces (5 8 9 10)  // Arbitrary numbering

If we now have a the address of the first entry (5) -> begin() function, the pointer's value will be 5. If we move the pointer forward with (lets say the integer has 16bits), the pointer will point to the address where the value 8 is stored. So the loop:

        for (label face=0; face<nFaces; face++)
        {
            HpsiPtr[uPtr[face]] -= lowerPtr[face]*psiPtr[lPtr[face]];
            HpsiPtr[lPtr[face]] -= upperPtr[face]*psiPtr[uPtr[face]];
        }

should do that. Now the question is, what array the lowerPtr() points to. As I get it, it points to the fluxes so it is finally that one:

face of Cell 1 has the faces (5 8 9 10)  // Arbitrary numbering
fluxes of Cell 1 based on face ordering (1.243  -12.353 1.529 8.982)

As you can see, it will get the correct fluxes
I think the drawing you made is somehow a bit misleading because here we would use the ID of the faces either than moving them forward with pointers and addresses.

In addition I tried to output the value of nFaces. Unfortunately the solvers icoFoam, simpleFoam and pimpleFoam are not calling this function so I do not know it exactly but as far as I understand, the variable face is an iterator through the flux list based on pointer and memory. Maybe it is not 100% correct what I told but it should be in that way... or if I would investigate more time, I will see that it is complete different. Due to the fact that there is no time, I hope that it is correct and help you. Furthermore based on the example you gave, the lower values should correspond to 0, 5 and the upper to 3 with respect to the cell 1.


The last thing you mentioned may be correct but I do not know the correct equation. So I can not tell you anything.

[Jerryfan]

Dear Tobi,


Thanks for your reply. I did make a mistake while I was copying and pasting. Sorry about this. This has been revised now. What I am trying to say is like this:

for (register label face=0; face<l.size(); face++)
{
Diag[l[face]] -= Upper[face];
Diag[u[face]] -= Lower[face];
}

As for the 2D mesh showed above, cell #1 is surrounded by face #0, #2 and #3. See the figure I attached here.



The loop inside the negSumDiag() function is controlled by face id rather than cell id, and the discretization coefficients contained in those Lower and Upper arrays are indexed by face id as well.
As I mentioned above, Diag[1] will be visited three times. They are when:
face=0, then u[0]=1 so that we have Diag[1], at the same time, Diag[1]-=Upper[0];
face=2, then l[2]=1 so that we have a second Diag[1], at the same time, Diag[1]-=Lower[2];
face=3, then l[3]=1 so that we have the third Diag[1], at the same time, Diag[1]-=Lower[3].

That's why in total, Diag[1]=-(Upper[0]+Lower[2]+Lower[3]) . But from the figure I attached above, it can be seen that Diag[1]=-(Lower[0]+Upper[2]+Upper[3]) . why? I attached another figure, which is the matrix of the discretization coefficients.



For cell #1, it's discretized equation will be: A10* T0 + A11* T1 + A12* T2 + A15 * T5 = b1 (For convenience, I just use T to represent the scalar variable we are solving). In the matrix, A10 corresponds to Lower[0], A12 corresponds to Upper[2] and A15 corresponds to Upper[3]. This can be found in the OpenFOAM guide/matrix. https://openfoamwiki.net/index.php/O...es_in_OpenFOAM

However, if we use the code below in the negSumDiag() function,

for (register label face=0; face<l.size(); face++)
{
Diag[l[face]] -= Upper[face];
Diag[u[face]] -= Lower[face];
}

It will be the same as what I expect.

[Jerryfan]

Too bad, the figures are not showing here. I don't know if you can see by right click and open it in another tab. If you cann't see it this way, I will think about other ways.

[Jerryfan]

The images are showing now.

[Jerryfan]

Dear Tobi,



It takes me quite a long time to prepare the above figures. Now let me explain what I mean for the lduMatrix::H function.

First of all, the array lowerPtr() points to is not the flux. It is still the discretization coefficients as I explained above. I have to say the Lower() and Upper() coefficients in OpenFOAM (off-diagonal coefficients) are calculated correctly. I've followed the source code, they are done in a very appropriate way. That's why you get the correct "flux" (it's in fact, off-diagonal coefficients). I only have some doubts about the diagonal coefficients calculation as I explained above.

What I am trying to point out here in the lduMatrix::H function is the indexes used for the HpsiPtr array.

If we write out the corresponding mathematic equations of the negSumDiag() and the code snippet in the lduMatrix::H (forget about the source terms for H now), they are equivalent to:



Let's still take the cell #1 in the 2D mesh above as an example.

for (label face=0; face<nFaces; face++)
{
HpsiPtr[uPtr[face]] -= lowerPtr[face]*psiPtr[lPtr[face]];
HpsiPtr[lPtr[face]] -= upperPtr[face]*psiPtr[uPtr[face]];
}

we know that HpsiPtr[1] will be visited three times. They are when (for convinience, I just use T to represent phi in the equation):
face=0, then uPtr[0]=1 so that we have HpsiPtr[1], at the same time, HpsiPtr[1]-=lowerPtr[0]*T[0]=A10*T[0];
face=2, then lPtr[2]=1 so that we have a second HpsiPtr[1], at the same time, HpsiPtr[1]-=upperPtr[2]*T[2]=A12*T[2];
face=3, then lPtr[3]=1 so that we have the third HpsiPtr[1], at the same time, HpsiPtr[1]-=upperPtr[3]*T[3]=A15*T[5].

In total, H[1] = -(A10*T[0]+ A12*T[2]+ A15*T[5]).
which is exactly what the equation represents.

However, if we follow the way how the negSumDiag() function handles the indexes for the Diag array, we should write the code this way:

for (label face=0; face<nFaces; face++)
{
HpsiPtr[lPtr[face]] -= lowerPtr[face]*psiPtr[lPtr[face]];
HpsiPtr[uPtr[face]] -= upperPtr[face]*psiPtr[uPtr[face]];
}

Isn't it? Correct me if I am wrong. This is the part that really confuses me now.

[Tobi]

Hi,

I think I am not the right guy for your question. If I have time, I will investigate into that but up to now no idea. Do you have some literature in addition? maybe I will check Ferziger.

By the way. When is th H function be called? as I checked out on Thursday, I did not figure out when this function is called.

Kind regards, tobi

[Zeppo]

Originally Posted by jerryfan

the thing that confuses me here is, should it be like this: ?

for (register label face=0; face<l.size(); face++)
    {
        diag[l[face]] -= upper[face];
        diag[u[face]] -= lower[face];
    }

Originally Posted by tobi

i think i am not the right guy for your question. If i have time, i will investigate into that but up to now no idea. Do you have some literature in addition? Maybe i will check ferziger.

I hope I don't violate any copiright law sharing a bit of information from a book. If any moderators think the other way please let me know and I will remove the copyrighted material from the post. Thanks.
The cite from Moukalled, Mangani, Darwish - The Finite Volume Method in Computational Fluid Dynamics An Advanced Introduction with OpenFOAM® and Matlab (Fluid Mechanics and Its Applications) - 2015; pages 201-202:

For the domain shown on the upper left side of Fig. 7.10, the owner and neighbor of each face are displayed in the lowerAddr() and upperAddr() array, respectively. The face number is the position of the owner or neighbor in the array plus one (since numbering starts with 0). Considering internal face number 4, for example, its related information is stored in the fifth row (in C++ indexing starts from 0) of the lower(), upper(), lowerAddr(), and upperAddr() array, respectively. The stored data indicate that its owner is element number 2 (lowerAddr() array), its neighbor is element number 4 (upperAddr() array), the coefficient multiplying phi_4 in the algebraic equation for element number 2 is stored in the fifth row of the array upper(), and the coefficient multiplying phi_2 in the algebraic equation for element number 4 is stored in the fifth row of the array lower().
lduAddressing.jpg
Fig. 7.10 The lduAddressing and lduMatrix

All that is followed by the allready mentioned code

for (label faceI=0; faceI<l.size(); faceI++)
{
    ac[l[faceI]] -= Lower[faceI];
    ac[u[faceI]] -= Upper[faceI];
}
Listing 7.52 Summation of the off-diagonal coefficients

which ridiculously contradicts the text it follows.

Originally Posted by tobi

by the way. When is th h function be called? As i checked out on thursday, i did not figure out when this function is called.

It might be a thing related to the H-operator used in SIMPLE algorithm

[yehaixuan]

Originally Posted by Jerryfan

Dear Foamers,


This question has been raised for several times at least here in this Forum. It seems that they all didn't give a clear answer. That's why I am trying to bring it up again.

http://www.cfd-online.com/Forums/ope...lculation.html

http://www.cfd-online.com/Forums/ope...ddtscheme.html (The #7)


http://www.cfd-online.com/Forums/ope...-operator.html

The calculation of the diagonal coefficients lots of times are done by the negSumDiag() function. The code is like this:

void Foam::lduMatrix::negSumDiag()
{
    const scalarField& Lower = const_cast<const lduMatrix&>(*this).lower();
    const scalarField& Upper = const_cast<const lduMatrix&>(*this).upper();
    scalarField& Diag = diag();

    const labelUList& l = lduAddr().lowerAddr();
    const labelUList& u = lduAddr().upperAddr();

    for (register label face=0; face<l.size(); face++)
    {
        Diag[l[face]] -= Lower[face];
        Diag[u[face]] -= Upper[face];
    }
}

The thing that confuses me here is, should it be like this: ?

for (register label face=0; face<l.size(); face++)
    {
        Diag[l[face]] -= Upper[face];
        Diag[u[face]] -= Lower[face];
    }

In santiagomarquezd's post, a 2D mesh was proposed: (Details were given in his post)

*-------*-------*-------*-------*
| 0 | 1 | 2 | 3 |
*-------*-------*-------*-------*
| 4 | 5 | 6 | 7 |
*-------*-------*-------*-------*

The calculation of diagonal coefficient for cell #1 is given in loops 0, 2 and 3 in the negSumDiag() function.

Loop #0:
Diag[u[0]] -= Upper[0]; (Equivalent to: Diag[1] -=Upper[0] )

Loop #2:
Diag[l[2]] -= Lower[2]; (Equivalent to: Diag[1] -=Lower[2] )

Loop #3:
Diag[l[3]] -= Lower[3]; (Equivalent to: Diag[1] -=Lower[3] )

In total,
Diag[1] = -(Upper[0] + Lower[2] + Lower[3])

This confuses me so much as it is very obvious that Diag[1] should be calculated as:
Diag[1] = -(Lower[0] + Upper[2] + Upper[3])

It might work for a symmetric matrix, but I really doubt about the non-symmetric case.
(correct me if I am wrong.)

The other thing that makes me even more confusing is the lduMatrix::H function.
The code:

template<class Type>
Foam::tmp<Foam::Field<Type> > Foam::lduMatrix::H(const Field<Type>& psi) const
{
    tmp<Field<Type> > tHpsi
    (
        new Field<Type>(lduAddr().size(), pTraits<Type>::zero)
    );

    if (lowerPtr_ || upperPtr_)
    {
        Field<Type> & Hpsi = tHpsi();

        Type* __restrict__ HpsiPtr = Hpsi.begin();

        const Type* __restrict__ psiPtr = psi.begin();

        const label* __restrict__ uPtr = lduAddr().upperAddr().begin();
        const label* __restrict__ lPtr = lduAddr().lowerAddr().begin();

        const scalar* __restrict__ lowerPtr = lower().begin();
        const scalar* __restrict__ upperPtr = upper().begin();

        register const label nFaces = upper().size();

        for (register label face=0; face<nFaces; face++)
        {
            HpsiPtr[uPtr[face]] -= lowerPtr[face]*psiPtr[lPtr[face]];
            HpsiPtr[lPtr[face]] -= upperPtr[face]*psiPtr[uPtr[face]];
        }
    }

    return tHpsi;
}

The part marked bold above means: (forget about the negtive sign in the code above and the source term below)



we see that it's not using:

for (register label face=0; face<nFaces; face++)
        {
            HpsiPtr[lPtr[face]] -= lowerPtr[face]*psiPtr[lPtr[face]];
            HpsiPtr[uPtr[face]] -= upperPtr[face]*psiPtr[uPtr[face]];
        }
    }

It's very strange. It seems the code contradicts itself in different usages.
Or there is some tricky part I didn't catch that makes these happen naturally.

Discussions on this are really needed.

I feel exactly the same way. Like in negSumDiag. For Diag[l[face]], it should use upper()[face] and lower() for Diag[u[face]].

But I guess I may misunderstand something, since all the places I can find these eqns write them in this way.

[me.ouda]

Originally Posted by Jerryfan

The thing that confuses me here is, should it be like this: ?

for (register label face=0; face<l.size(); face++)
    {
        Diag[l[face]] -= Upper[face];
        Diag[u[face]] -= Lower[face];
    }

I think think this is not correct. This implies that the diagonal coefficient in one row = - sum of all off-diagonal coefficient in the SAME row which is NOT correct. This is only valid if the equation is a pure diffusion equation (in this case both methods will be correct because the matrix is symmetric)

In case of advection-diffusion equation the negSumDiag function use this smart trick to avoid calculating the diagonal coefficient again, alternatively it assemble it from the off-diagonal coefficients of the neighboring cells.

Hope that helps.
Kind regards.

[Zeppo]

Originally Posted by me.ouda

I think think this is not correct. This implies that the diagonal coefficient in one row = - sum of all off-diagonal coefficient in the SAME row which is NOT correct.

Why? void Foam::lduMatrix::negSumDiag() is supposed to do a negative summation of the off-diagonal coefficients for each diagonal coefficient (each row in a matrix), isn't it? For each row you should only operate with coefficients in the same row.

[me.ouda]

Originally Posted by Zeppo

Why? void Foam::lduMatrix::negSumDiag() is supposed to do a negative summation of the off-diagonal coefficients for each diagonal coefficient (each row in a matrix), isn't it? For each row you should only operate with coefficients in the same row.

Why you suppose so? IMHO, that isn't correct. What this function supposed to do is to reconstruct the diagonal coefficients from the pre-calculated off-diagonal coefficients (to avoid overhead). This is clear in the code of lduMatrixOperations.C:

scalarField& Diag = diag();

To get the diagonal coefficient in one row you are NOT supposed to sum the off-diagonal coefficients in the same row. This is only true of you solve a pure diffusion equation. If the advection term is there then the this indeed not true.

Again this function do this smart trick to get the correct off-diagonal coefficient, namely coefficient from the corresponding neighbouring cell.

Please correct me if this isn't true.

Best regards.

[Zeppo]

Originally Posted by me.ouda

Again this function do this smart trick to get the correct off-diagonal coefficient, namely coefficient from the corresponding neighbouring cell.

By definition, for a specific diagonal coefficient A_ii, coefficients from the corresponding neighbouring cells are A_ij, not A_ji.

[Giantsda]

So I have written several lines of codes to construct a matrix and then call negSumDiag() to illustrate this problem and our confusion.

My mesh has 8 elements:
int de; // for pause the program so I can read the output.
scalarField& lower = UEqn.lower ();
scalarField& diag = UEqn.diag ();
scalarField& upper = UEqn.upper ();

forAll (diag,i){
diag[i]=0;
}

forAll (upper,i){
upper[i]=i+8;
}

forAll (lower,i){
lower[i]=i+20;
}

Info << "diag \n" << diag << "upper\n" << upper << "lower" << lower;
const lduAddressing & ldu = UEqn.lduAddr ();
const labelUList& lo = ldu.lowerAddr ();
const labelUList& up = ldu.upperAddr ();

Info<<"lo:\n"<<lo<<"up:\n"<<up;
scanf ("%d", &de); // input a int to go on.
UEqn.negSumDiag();
Info << "diag \n" << diag << "upper\n" << upper << "lower" << lower;
scanf ("%d", &de);
************************************************** ********************output************************ *
diag
8{0} // diag is all 0.

upper

12
(
8
9
10
11
12
13
14
15
16
17
18
19
)
lower
12
(
20
21
22
23
24
25
26
27
28
29
30
31
)
lo:

12
(
0
0
0
1
1
2
2
3
4
4
5
6
)
up:

12
(
1
2
4
3
5
3
6
7
5
6
7
7
)

So after setting values to the matrix stored in UEqn. Before UEqn.negSumDiag(); it is:
0.0 8.0 9.0 0 10.0 0 0 0
20.0 0.0 0 11.0 0 12.0 0 0
21.0 0 0.0 13.0 0 0 14.0 0
0 23.0 25.0 0.0 0 0 0 15.0
22.0 0 0 0 0.0 16.0 17.0 0
0 24.0 0 0 28.0 0.0 0 18.0
0 0 26.0 0 29.0 0 0.0 19.0
0 0 0 27.0 0 30.0 31.0 0.0
Lets look at the matrix values after UEqn.negSumDiag();
It is :
-63.0 8.0 9.0 0 10.0 0 0 0
20.0 -55.0 0 11.0 0 12.0 0 0
21.0 0 -60.0 13.0 0 0 14.0 0
0 23.0 25.0 -51.0 0 0 0 15.0
22.0 0 0 0 -67.0 16.0 17.0 0
0 24.0 0 0 28.0 -58.0 0 18.0
0 0 26.0 0 29.0 0 -62.0 19.0
0 0 0 27.0 0 30.0 31.0 -52.0

-63=-20-21-22;
-55=-8-23-24;
and so on;

I know the matrix is correctly printed because I am using gdbOF to print it. ( pfvMatrixFull UEqn f1, handy tool it you have not tried yet.)
So my confusion is :
UEqn.negSumDiag() sums the value in the same column for all diag components but not rows.
This confuses me a lot. I think it should sum for the row because each row describe the relationship of each cell and its neighbors, not column,

Tell me if the above is not clear and I will make it clear.

Lets try to finish and close this question.

Chen

[Giantsda]

I think I have figured this out:
1. void Foam::lduMatrix::negSumDiag() is negative sum its column , not its rows and then put the value to each diagonal entry.
This can be confirmed by adding:
fvScalarMatrix div (fvm::div (phi, T)); to almost any case
and print the matrix of div and view it. The value of each diagonal entry is its negsum of its column.

2. Now for the question why we should sum for columns, not for rows, I did a simple case. The index is 1 based.



and the matrix A is:




Chen