 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear all,
I have a question to you all and hope that someone can clarify everything. What I am calculating is nothing special. It is just the temperature distribution inside a solid. Basically it is just the Laplace equation with the time derivative. However, I will show you how I got to the equation and what I figured out which I do not really understand. Enthalpy equation I started the derivation of the temperature equation by using the common enthalpy equation: 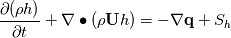 Based on the fact that I have a solid, there is no convection. In addition, further source terms 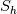 are not considered. Only the thermal conduction are not considered. Only the thermal conduction 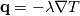 is considered. Thus we get to the simple equation: is considered. Thus we get to the simple equation: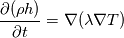 The problem that I had is to replace the enthalpy with the temperature. We know that: 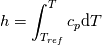 Okay, now I split the time derivative using the product rule: 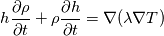 Now I extended the second term as: 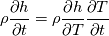 I think we can change the partial derivative to finite differences - that should not be a big deal ( 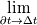 ) but please correct me if I am wrong here: ) but please correct me if I am wrong here: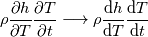 inserting the definition of the enthalpy we get: ![\rho\frac{\mathrm{d} h}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t}
=
\rho\frac{\mathrm{d} \left[\int_{T_{ref}}^{T} c_p \mathrm{d}T\right]}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t} = \rho c_p \frac{\mathrm{d} T}{\mathrm{d} t}
\longrightarrow
\rho c_p \frac{\partial T}{\partial t} \rho\frac{\mathrm{d} h}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t}
=
\rho\frac{\mathrm{d} \left[\int_{T_{ref}}^{T} c_p \mathrm{d}T\right]}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t} = \rho c_p \frac{\mathrm{d} T}{\mathrm{d} t}
\longrightarrow
\rho c_p \frac{\partial T}{\partial t}](/Forums/vbLatex/img/b4808deb37c2d7f9ce315188043feec1-1.gif) Summing up I got: 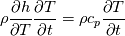 Inserting it to the enthalpy equation we get the following: 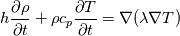 The first term vanishes based on the continuity equation which should hold always (right?): (Note... I was writing the continuity equation wrong - corrected now) 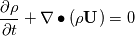 Based on the fact that there is no velocity 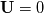 , all terms vanishes. To be more precise, the convective term vanishes and we get: , all terms vanishes. To be more precise, the convective term vanishes and we get: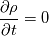 Therefore, the first term in the new enthalpy equation vanishes and we get: 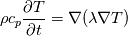 Till now, I did not assume that the density neither the heat capacity or the thermal conductivity is constant. So the first question is, is that derivation correct? Implementation I made simple checks in order to check out the temperature distributions. What I did is the following. I solved the three different kind of equations: Code:
//- No convergence after 10 Outer loops
// After the third outer loop, the initial residual stays constant (~ 0.0042)
fvScalarMatrix TEqn
(
rho*cp*fvm::ddt(T)
==
fvm::laplacian(k, T)
);
TEqn.solve()
Info<< "T[10] -> " << T[10] << endl;
Code:
//- No convergence after 10 Outer loops
// After the third outer loop, the initial residual stays constant (~ 0.0042)
// Same as above
fvScalarMatrix TEqn
(
fvm::ddt(rho*cp, T)
==
fvm::laplacian(k, T)
);
TEqn.solve()
Info<< "T[10] -> " << T[10] << endl;
Code:
//- Convergence after 4 iterations to 1e-10
fvScalarMatrix TEqn
(
fvm::ddt(T)
==
fvm::laplacian(k/rho/cp, T)
);
TEqn.solve()
Info<< "T[10] -> " << T[10] << endl;
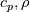 and put it inside the Laplace term? From a mathematical point I am not sure. Okay, these quantities are temperature depended and the Laplace operator (or gradient/divergence) is space operator. However, based on the temperature distribution these quantities are somehow space depended too. and put it inside the Laplace term? From a mathematical point I am not sure. Okay, these quantities are temperature depended and the Laplace operator (or gradient/divergence) is space operator. However, based on the temperature distribution these quantities are somehow space depended too. The third question is, why are the first and second implementation not converging while the third one does? Any help would be highly appreciated and it would be nice if someone can check my derivation. I am really not sure about that. Thank you in advance, Kind regards, Tobi
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; March 9, 2017 at 06:10. Reason: Wrong continuity equation / change #2 |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
A . B = 0 and A = 0
does not imply that B = 0 too. so i do not understand how you get d rho / d t = 0 from u = 0. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Sergei
Join Date: Dec 2009
Posts: 261
Rep Power: 21  |
You didn't post the results you've gotten from the code runs
Code:
Info<< "T[10] -> " << T[10] << endl; Look at the source code. Code:
rho*cp*fvm::ddt(T) Code:
new GeometricField<Type, fvPatchField, volMesh>
(
io,
rho*cp * 1.0/mesh().time().deltaT() *(T - T.oldTime())
)
Code:
fvm::ddt(rho*cp, T) Code:
new GeometricField<Type, fvPatchField, volMesh>
(
io,
1.0/mesh().time().deltaT() * (rho*cp*T - (rho*cp).oldTime()*T.oldTime())
)
Quote:
|
||
|
|

|
||
|
|
|
#4 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hey Arjun,
you are right and I was too stupid to write the correct continuity equation. I corrected it now and you can see that the derivation should be correct. Thanks for mentioning it (indirectly). Edit based on the reply from Zeppo You are right, again I made a mistake. I was using wrong words. I did not want to say converged and not converged but the matrix system (the residual error) does not get smaller anymore (comparing the first two implementations and the last one). That 's what I wanted to say. Tomorrow I will make an analysis of the absolute values and post it. As far as I have it in mind, #1 and #2 were similar where #3 was different (but only ~ 0.3K).
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; March 8, 2017 at 03:31. Reason: Updated based on wrong continuity equation in the first post |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Sergei
Join Date: Dec 2009
Posts: 261
Rep Power: 21  |
||
|
|

|
|
|
|
|
#6 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear Sergei,
thanks for the hint. I will check it out, perfect! Thank you again.
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; October 14, 2017 at 07:03. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Why can not you use the very first equation you wrote, the enthalpy equation?
|
|
|
|

|
|
|
|
|
#8 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hi Arjun,
I could do but I am just interested in the temperature distribution in my solid body and I do not want to recalculate the temperature based on the enthalpy. Well FOAM offers the recalculation but I wanted to keep my solver as simple as possible. Never checked out the code how FOAM recalculate T from h and vice versa.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#9 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
Its alright. I use the equation based on total energy and total enthalpy in wildkatze and directly calculate the temperature from it without recalculating from enthalpy. What you do is cheaper though, no doubt. I did that way because it can accommodate most of the things ie solids u, p etc terms gone, in case of fluids taken care. The same could be used in combustion (i am in process of coding now), same could be used with user defined gas law for example. PS: Last 1 month I am learning and trying to code combustion it is fun :-) So I am getting into that stiff ODE problem now. |
||
|
|

|
||
|
|
|
#10 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hi Arjun,
Offtopic I am dealing with combustion since 3 years. Maybe you know that I am developing a flamelet creator. The only missing part is solving the Stiff ODE. Unfortunately I made my own C++ project to learn much more in OOP but now I cannot use the ODE solvers from FOAM like, SEULEX, RODOS etc. Well, I hope that one day I can implement into my code. If you want to contribute, you are welcomed. Topic I agree that in fluids it would be nice calculating the enthalpy. As you already said, I just calculate the temperature because it is cheaper and I do not solve other stuff (only thermal stress). However, if someone is interested, I made a simple test case (attached - you have to modify it to e.g. laplacianFoam). However, I checked the different temperature implementations named 1, 2, 3 , 4 and 5 in the charts. The implementation was as follows: Code:
// Calculated marked with 1 rho*cp*fvm::ddt(T) == laplacian(k, T) // Calculated marked with 2 cp*fvm::ddt(rho, T) == laplacian(k, T) // Calculated marked with 3 fvm::ddt(cp*rho, T) == laplacian(k, T) // Calculated marked with 4 fvm::ddt(cp*rho, T) - rho*T*fvc::ddt(cp) == laplacian(k, T) // Calculated marked with 5 fvm::ddt(T) == laplacian(k/rho/cp, T) Thank you Zappo for the hint. I will use implementation (2) for now.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#11 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
I am at the moment working on finite rate species combustion and now I start to work on ERENA algorithm and VODE based stiff solver (after ERENA) (will compare the two on cost of calculation). I created a project called firekatze around these things like flamelets and other combustion related things (I added chemkin import and transport properties import etc). Shall provide you then species properties from temperature and pressure. At the moment the focus is to get this combustion thing work on finite rate and it shall be faster. Made lots of change to accomodate it in FVUS (like explicit navier stokes for example) PS: I learned all that in last 30 days, i remember i started on 7th feb and its 8th now. So huge amount of code i did in this month, still going on. |
||
|
|

|
||
|
|
|
#12 | |
|
Senior Member
Sergei
Join Date: Dec 2009
Posts: 261
Rep Power: 21  |
Quote:
|
||
|
|

|
||
|
|
|
#13 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
I was also thinking about decreasing the time step and increasing the outer loops. But I wanted to have Same settings. Well, tomorrow I will Check it out.
Sent from my HTC One mini using CFD Online Forum mobile app
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#14 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
I posted wrong results here because the last check yesterday was with constant values (cp, rho, k). Thats the reason why 4 was not blowing up. New results are in preparation.
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; March 9, 2017 at 05:02. Reason: Used constant values - wrong results |
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
Agustín Villa
Join Date: Apr 2013
Location: Alcorcón
Posts: 314
Rep Power: 15  |
||
|
|

|
|
|
|
|
#16 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Yes you are right. The rho should be considered. Typing all the equations in here is sometimes a bit ... wired. I will change it. However, in the literature Zappo is mentioning, you will find the derivation. However, I don't know where the mistake in my derivation is. The difference that I can point out at the moment is that Moukalled et al. use the total derivative which then lead the the density inside. What I mean is, that I was doing that:
![\rho\frac{\mathrm{d} h}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t}
=
\rho\frac{\mathrm{d} \left[\int_{T_{ref}}^{T} c_p \mathrm{d}T\right]}{\mathrm{d} T}\frac{\mathrm{d} T}{\partial t} =\rho c_p \frac{\mathrm{d} T}{\mathrm{d} t}
\longrightarrow
\rho c_p \frac{\partial T}{\partial t} \rho\frac{\mathrm{d} h}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t}
=
\rho\frac{\mathrm{d} \left[\int_{T_{ref}}^{T} c_p \mathrm{d}T\right]}{\mathrm{d} T}\frac{\mathrm{d} T}{\partial t} =\rho c_p \frac{\mathrm{d} T}{\mathrm{d} t}
\longrightarrow
\rho c_p \frac{\partial T}{\partial t}](/Forums/vbLatex/img/da2242315a8aa85bc8b9ed2d42c63b93-1.gif) While Moukalled was getting the total derivative: 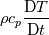 It is clear why the density is inside the derivative if we rearrange the equation without the total derivative. I don't know, maybe I was missing something or my assumption I made with the lim is not correct. I might miss some important thing. By the way there is a typo on page 62 in equation 3.67. DP -> Dp. Summing up: Moukalled et al. replaced: 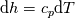 into the total derivative of the enthalpy: 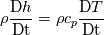 and I used the lim to go from finite differences to partial differential stuff. So I think there I made a mistake. To be honest, I am not sure if am allowed to do what I did. Would be nice if someone can check it and tell the mistake. Note: I changed the equations above related to the mistake I made (rho missing). Remark: (not correct - see my next post. Everything is fine) After checking the first post, the difference comes from this line: ![\rho\frac{\mathrm{d} h}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t}
=
\rho\frac{\mathrm{d} \left[\int_{T_{ref}}^{T} c_p \mathrm{d}T\right]}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t} = \rho c_p \frac{\mathrm{d} T}{\mathrm{d} t}
\longrightarrow
\rho c_p \frac{\partial T}{\partial t} \rho\frac{\mathrm{d} h}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t}
=
\rho\frac{\mathrm{d} \left[\int_{T_{ref}}^{T} c_p \mathrm{d}T\right]}{\mathrm{d} T}\frac{\mathrm{d} T}{\mathrm{d} t} = \rho c_p \frac{\mathrm{d} T}{\mathrm{d} t}
\longrightarrow
\rho c_p \frac{\partial T}{\partial t}](/Forums/vbLatex/img/b4808deb37c2d7f9ce315188043feec1-1.gif) Especially this one:  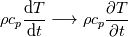 Which should be wrong based on Moukalled et al. because he related it to the total Derivative:  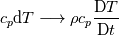
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; February 16, 2018 at 07:54. Reason: Remark might be not be decribed well |
|
|
|

|
|
|
|
|
#17 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
If possible just name the functions something like this void Function( arguements ) ... for the things that you would want so I would create them into library. That way it would save you lot of headache. Also know that firekatze can load chemkin, so if would want it would give you other things like diffusion coefficients of species, enthalphy , conductivity, viscosity etc of species etc etc. So when you get time, just prepare a note what things you wish and library shall have it. PS: At the moment i am using chemkin and transport data produced from http://akrmys.com/KUCRS/index.htm.en |
||
|
|

|
||
|
|
|
#18 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Offtopic:
Hi Arjun, I made my own code that loads chemistry, transport and thermodynamic data. The code reads a dictionary where the user can specify the fuel and oxidizer stream and other solver related stuff. After that, I construct the polynomials for fitting (viscosity, thermal conductivity, binary diffusion etc.). However, the user can specify the calculation of the gas kinetic equation and if he want to use fitting procedure or direct calculation. Then I build my flamelet class with all information which then should solve everything. Everything is already implemented, TROE, LOW, ENHANCED, SRI ... but the only thing that is missing is the solving of the chemistry. I was thinking of using sub-time stepping, like flamelet equation dt and then solve chemistry with an ODE in order to reach that dt. After that go to the next time step (I think it is a common approach). At the moment (or 3 weeks ago) I started to implement simple Euler Integration which is easy but not really powerful. However, doing that, I would have the basis of other solver implementations. But like always - no time. So the project is stlil at the moment. If you are interested: http://afc.holzmann-cfd.de/ but it is outdated. If you want, I can upload the latest doxygen stuff today evening. Topic Just want to inform you that everything is fine and the equation I derived at the beginning is correct within my assumptions. As Zeppo mentioned, the temperature equation is given in Moukalled et al. However, as I pointed out above, I got a different equation which is in fact correct because I do not have any velocities. Therefore, taking the equation from Moukalled et al. and applying my assumptions (no motion -> no velocity): ![c_p \left[ \frac{\partial \rho T}{\partial t} + \nabla \bullet (\rho \textbf{U} T) \right] = \nabla \bullet (k \nabla T) c_p \left[ \frac{\partial \rho T}{\partial t} + \nabla \bullet (\rho \textbf{U} T) \right] = \nabla \bullet (k \nabla T)](/Forums/vbLatex/img/3200a65038f90b34a81e6b4192c64aa3-1.gif) ![c_p \left[ \rho \frac{\partial T}{\partial t} + T \frac{\partial \rho}{\partial t} + \rho \textbf{U} \bullet \nabla T + T \nabla \bullet (\rho \textbf{U}) \right] = \nabla \bullet (k \nabla T) c_p \left[ \rho \frac{\partial T}{\partial t} + T \frac{\partial \rho}{\partial t} + \rho \textbf{U} \bullet \nabla T + T \nabla \bullet (\rho \textbf{U}) \right] = \nabla \bullet (k \nabla T)](/Forums/vbLatex/img/853437a87d2fa855af0f86d5cd99dcb8-1.gif) ![c_p \left[ \rho \frac{\partial T}{\partial t} + \rho \textbf{U} \bullet \nabla T + T \left\{ \underbrace{\frac{\partial \rho}{\partial t} + \nabla \bullet (\rho \textbf{U})}_{\text{continuity}}\right\} \right] = \nabla \bullet (k \nabla T) c_p \left[ \rho \frac{\partial T}{\partial t} + \rho \textbf{U} \bullet \nabla T + T \left\{ \underbrace{\frac{\partial \rho}{\partial t} + \nabla \bullet (\rho \textbf{U})}_{\text{continuity}}\right\} \right] = \nabla \bullet (k \nabla T)](/Forums/vbLatex/img/5bb45d42cbcdb89967245baeb32d0804-1.gif) 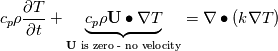 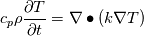 Thats the reason why the calculations of the temperature of 1 and 3 are almost similar. I hope that this is the proof and everybody would agree.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#19 |
|
New Member
Hasan Shetabivash
Join Date: Jan 2017
Location: Montreal
Posts: 17
Rep Power: 12  |
Dear Tobias,
First of all assuming constant density and heat capacity for solids is reasonable and the energy equation you've obtained for solid is acceptable (see the book by Moukalled page 65 Eq. 3.80). The difference between your mathematical operations with those of Moukalled is the fact that zero velocity was your foremost assumption and you derived all the equations based on the zero velocity in the domain. However, in the book the zero velocity was the last assumption which lead to your final equation. The only thing that you need to consider is non-linearity that is added to the equation by dependence of Cp to temperature. If Cp(T) is changing dramatically you need an appropriate method to deal with the nonlinear problem. Cheers, |
|
|
|

|
|
|
|
|
#20 |
|
Member
Karelke Yu
Join Date: Dec 2014
Posts: 96
Rep Power: 11  |
Hi Tobi,
I am facing the same situation here, planning to solve a temperature equation as yours but with flow U. Is it possible for u to share your solution/code here setting us a valuable example? I think foamer struggling with the same situation will appreciate great thanks to you. Best, Karekle |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Static Temperature / Opening Temperature | JulianP | CFX | 12 | April 10, 2019 18:00 |
| Multiphase flow - incorrect velocity on inlet | Mike_Tom | CFX | 6 | September 29, 2016 01:27 |
| Constant velocity of the material | Sas | CFX | 15 | July 13, 2010 08:56 |
| temperature equation for one phase in multiphase solver | romant | OpenFOAM Programming & Development | 0 | April 13, 2010 05:06 |
| Adding temperature equation in settlingFoam | sachin | OpenFOAM Running, Solving & CFD | 2 | March 31, 2010 03:21 |