 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Sam Maloney
Join Date: Aug 2018
Location: Zürich, Switzerland
Posts: 2
Rep Power: 0  |
I am trying to understand the time-marching scheme that is implemented in the dbnsFoam (and dbnsTurbFoam) solvers in foam-extend (I am using version 4.0).
The solver source file specifies it only as a "explicit time-marching" scheme and in my googling around, I found on page 11 of this presentation by Jemcov et al. [1] a reference to this paper by Arnone et al. [2] which says that the scheme should look like the following:  where 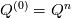 and and 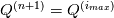 and and 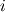 specifies the stage of the Runge-kutta scheme. One difference, however, is that the coefficients used in the code appear to be specifies the stage of the Runge-kutta scheme. One difference, however, is that the coefficients used in the code appear to be ![\beta_i=[0.11, 0.2766, 0.5, 1] \beta_i=[0.11, 0.2766, 0.5, 1]](/Forums/vbLatex/img/324b088f41a82c665266703935756031-1.gif) , while the paper [2] appears to specify , while the paper [2] appears to specify ![\beta_i=[1/4, 1/3, 1/2, 1] \beta_i=[1/4, 1/3, 1/2, 1]](/Forums/vbLatex/img/e4ee224e004475206bec708f6ad8151e-1.gif) . If anyone knows a reference for why these coefficients were chosen, that would be great? . If anyone knows a reference for why these coefficients were chosen, that would be great?However, my bigger question comes when looking at the code itself in dbnsFoam.C, it looks like this: Code:
forAll (beta, i)
{
// Solve the approximate Riemann problem for this time step
dbnsFlux.computeFlux();
// Time integration
solve
(
1.0/beta[i]*fvm::ddt(rho)
+ fvc::div(dbnsFlux.rhoFlux())
);
solve
(
1.0/beta[i]*fvm::ddt(rhoU)
+ fvc::div(dbnsFlux.rhoUFlux())
);
solve
(
1.0/beta[i]*fvm::ddt(rhoE)
+ fvc::div(dbnsFlux.rhoEFlux())
);
# include "updateFields.H"
}
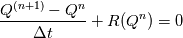 so in the above code it seems to me that it would produce update equations at each iteration of the for loop that look like:  which differs from the original form in [1] and [2] in that the first RHS term is 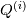 instead of instead of 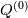 . .My question then is whether I am missing something in my understanding of how the solve operation works? It seems like on the first iteration of the for loop, the convervative variables rho, rhoU, and rhoE should be updated to the 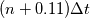 timestep and then the code in updateFields.H will update the remaining primitive variables. Thus on the next for loop iteration, the original timestep and then the code in updateFields.H will update the remaining primitive variables. Thus on the next for loop iteration, the original 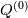 was not saved anywhere, so it will have to use was not saved anywhere, so it will have to use 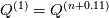 instead. instead.If anyone can shed light on what I might be missing here it would be most appreciated! [1] Density Based Navier Stokes Solver for Transonic Flows, https://pdfs.semanticscholar.org/pre...499886bb04.pdf [2] Multigrid time-accurate integration of Navier-Stokes equations, https://ntrs.nasa.gov/search.jsp?R=19940012785 |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Sam Maloney
Join Date: Aug 2018
Location: Zürich, Switzerland
Posts: 2
Rep Power: 0  |
Alright, so after more digging through code and documentation, I have learned that the "GeometricField" class has a member "oldTime()" (and some other associated methods) which allow it to automatically store old values in the background during the solve operation. The Euler ddt scheme uses this oldTime() value to build its discretization, and since the time index is only incremented after all four Runge-Kutta stages have completed, this means it is indeed
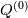 and not and not 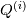 which appears on the RHS of the update equation, giving the desired form shown in the references. which appears on the RHS of the update equation, giving the desired form shown in the references.Therefore my only remaining question is the motivation for the choice of the ![\beta_i=[0.11, 0.2766, 0.5, 1] \beta_i=[0.11, 0.2766, 0.5, 1]](/Forums/vbLatex/img/324b088f41a82c665266703935756031-1.gif) coefficients? If anyone knows a reference for these values, or has any other information on their properties (order of accuracy, is it SSP?, ...) that would be very helpful! coefficients? If anyone knows a reference for these values, or has any other information on their properties (order of accuracy, is it SSP?, ...) that would be very helpful!
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Mar 2016
Posts: 3
Rep Power: 10  |
Hi, I've found only one paper with these coefficients so far. Try this, page 14:
https://www.researchgate.net/publica...uler_equations It seems like the first two coefficients 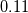 and and 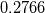 are result of trial and error around the classical coefficients are result of trial and error around the classical coefficients 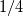 and and  which cause bigger stability region of four-stage Runge-Kutta scheme. which cause bigger stability region of four-stage Runge-Kutta scheme.Hope this helps. |
|
|
|

|
|
 |
| Tags |
| dbnsfoam, extend 4.0, foam-extend, foam-extend 4.0, runge-kutta |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [Other] Contribution a new utility: refine wall layer mesh based on yPlus field | lakeat | OpenFOAM Community Contributions | 58 | December 23, 2021 02:36 |
| pimpleDyMFoam computation randomly stops | babapeti | OpenFOAM Running, Solving & CFD | 5 | January 24, 2018 05:28 |
| High Courant Number @ icoFoam | Artex85 | OpenFOAM Running, Solving & CFD | 11 | February 16, 2017 13:40 |
| [solidMechanics] solidMechanics gear contact in rotation | nlc | OpenFOAM CC Toolkits for Fluid-Structure Interaction | 3 | January 11, 2015 06:41 |
| Star cd es-ice solver error | ernarasimman | STAR-CD | 2 | September 12, 2014 00:01 |