 |
|
|
[Sponsors] | |||||
Why are the rotational transformation tensors in transform.H transposed? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Join Date: Sep 2018
Posts: 53
Rep Power: 7  |
Hi all,
The rotational transformation tensors in transform.H seem to be the transpose of the actual transformation tensors. For example: Code:
//- Rotational transformation tensor about the z-axis by omega radians
inline tensor Rz(const scalar& omega)
{
const scalar s = sin(omega);
const scalar c = cos(omega);
return tensor
(
c, s, 0,
-s, c, 0,
0, 0, 1
);
}
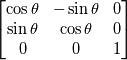 I checked multiple versions of OpenFoam and they all do the same thing. Why is this? |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Mark Olesen
Join Date: Mar 2009
Location: https://olesenm.github.io/
Posts: 1,714
Rep Power: 40   |
Quote:
It is best phrased as a question of perspective. Does the transform represent how to get from a global coordinate orientation to a local coordinate orientation, or how to get from a local coordinate orientation to a global one? If you can be content with "transform" meaning "how do I transform to get everything into the global reference?", it seems OK. The axesRotation.C might make the local/global relationship clearer. https://develop.openfoam.com/Develop...otation.C#L128 |
||
|
|

|
||
|
|
|
#3 |
|
Member
Join Date: Sep 2018
Posts: 53
Rep Power: 7  |
Ah, I think I understand now. I was thinking in terms of transforming a vector, not the coordinate system. Thank you very much.
|
|
|
|

|
|
 |
| Tags |
| rotation, rotation tensor, transform, transformation tensor |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Material change during phase transformation (FePO4 > LiFePO4) concentration distribut | kimsw0103 | CFX | 0 | January 15, 2016 22:05 |