 |
|
|
[Sponsors] | |||||
Implementation of turbulent algebraic heat flux model |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Jan 2021
Posts: 10
Rep Power: 5  |
Hello dear community.
I want to implement an algebraic heat flux model, based on the one described in the StarCCM+ user guide, called Temperature Flux Model here, in OpenFOAM 8. The model is based on eddy viscosity models and needs to be implemented in a low-Re model. However, I start with an implementation in the standard k-epsilon model of OpenFOAM 8. In OpenFOAM, if I understand correct, the heat flux is calculated, based on Boussinesq approximation, by: 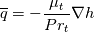 (1) (1)In comparison for the Temperature Flux Model, the heat flux is defined as: 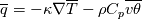 (2) (2)with 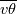 being the turbulent heat flux, which is given as: being the turbulent heat flux, which is given as: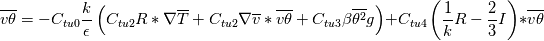 (3) (3)In order to calculate the turbulent heat flux 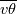 , a third transport equation for the temperature variance , a third transport equation for the temperature variance 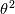 needs to be solved. The transport equation for the temperature variance is very similar to the transport equation of the turbulent kinetic energy k and is defined as: needs to be solved. The transport equation for the temperature variance is very similar to the transport equation of the turbulent kinetic energy k and is defined as:![\frac{\partial}{\partial t}\left(\rho \theta ^2\right)+\nabla * \left(\rho\theta^2\overline{v}\right)=\nabla * \left[\left(\mu+\frac{\mu_t}{\sigma_{\theta^2}}\right)\nabla\overline{\theta^2}\right]+G_\theta-\rho\epsilon_\theta \frac{\partial}{\partial t}\left(\rho \theta ^2\right)+\nabla * \left(\rho\theta^2\overline{v}\right)=\nabla * \left[\left(\mu+\frac{\mu_t}{\sigma_{\theta^2}}\right)\nabla\overline{\theta^2}\right]+G_\theta-\rho\epsilon_\theta](/Forums/vbLatex/img/75c2bb0895c4f23d7ca8b7a201b8be40-1.gif) (4) (4)with the production term of the temperature variance: 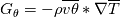 (5) (5)Furthermore, the temperature variance dissipation rate 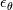 is defined via the thermal time scale is defined via the thermal time scale 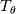 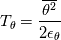 (6) (6)and the assumption of a constant turbulent-to-thermal time-scale ratio: 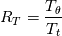 (7) (7)I have almost finished the implementation of the transport equation (4). Only the production therm (5) of the temperature variance is missing: Code:
// Temperature variance equation
tmp<fvScalarMatrix> theta2Eqn
(
fvm::ddt(alpha, rho, theta2_)
+ fvm::div(alphaRhoPhi, theta2_)
- fvm::laplacian(alpha*rho*Dtheta2Eff(), theta2_)
==
// production of theta2 is missing
- (alpha()*rho*theta2_)/(2*R_*turbTimeScale()) // epsilonTheta2
+ theta2Source()
+ fvOptions(alpha, rho, theta2_)
);
EDIT: Access to T: Code:
const volScalarField& T_ = this->mesh_.objectRegistry::template lookupObject<volScalarField>("T");
Furthermore, I am not sure, how I could implement equation (3). I have already defined model constants, but how can I get the Reynolds stress tensor and the thermal expansion coefficient here? If any further information is needed, please let me know. Thanks a lot in advance! Last edited by Fabio1893; January 8, 2021 at 07:38. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
Dear Fabio,
I implemented exactly this model in OpenFOAM (7). A German description can be found at https://www.grs.de/sites/default/files/pdf/grs-553.pdf, https://www.grs.de/publikationen/grs-553 Regarding your question about your equation (3). It is the "algebraic" equation which needs to be solved as matrix equation. So you have to re-arrange it into A x = b. As code, this looks like: Code:
thetaU_ = inv(leftSide) & rightSide; Joachim P.S. Are you somehow working together with NRG? |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Join Date: Jan 2021
Posts: 10
Rep Power: 5  |
Quote:
Dear Joachim, thank you for your reply! First of all, I want to mention that I have implemented now the thermal expansion coefficient beta, which is looked up and interpolated from a table, dependent on the temperature, which is important for my case, since I want to simulate heat transfer close to the critical point. I try to solve the equation (3) like this: Code:
// Turbulent heat flux equation
tmp<fvScalarMatrix> thfEqn
(
thf_
==
- Ctu0_*(k()/epsilon())*(Ctu1_*this->sigma()*fvc::grad(T_) + Ctu2_*dev(twoSymm(fvc::grad(U)))*thf()+Ctu3_*beta_*theta2()*g)
//+ Ctu4_*RSTanisotropy*thf()
);
thfEqn.ref().relax();
fvOptions.constrain(thfEqn.ref());
solve(thfEqn);
So re-arranging the equation, like you have written, would solve the problem, but still I do not totally understand how to do that. Could you explain, how to re-arrange the terms into A x = b a little more detailed please? Furthermore, I have a second question. I have implemented the transport equation for the temperature variance like that: Code:
// Temperature variance equation
tmp<fvScalarMatrix> theta2Eqn
(
fvm::ddt(alpha, rho, theta2_)
+ fvm::div(alphaRhoPhi, theta2_)
- fvm::laplacian(alpha*rho*Dtheta2Eff(), theta2_)
==
-1*alpha()*rho*thf_*mag(fvc::grad(T_)) // production of theta2
- (alpha()*rho*theta2_)/(2*R_*turbTimeScale()) // epsilonTheta2
+ theta2Source()
+ fvOptions(alpha, rho, theta2_)
);
Code:
-1*alpha()*rho*thf_*fvc::grad(T_) Code:
-1*alpha()*rho*thf_*mag(fvc::grad(T_)) EDIT (SOLVED): of course, thf_ needs to be a volVectorField. Therefore the temperature variance can be implemented as follows: Code:
// Temperature variance equation
tmp<fvScalarMatrix> theta2Eqn
(
fvm::ddt(alpha, rho, theta2_)
+ fvm::div(alphaRhoPhi, theta2_)
+ alpha()*rho*thf_&fvc::gradT_) // production of theta2
+ alpha()*(rho*theta2_)/(2*R_*turbTimeScale()) // epsilonTheta2
==
fvm::laplacian(alpha*rho*Dtheta2Eff(), theta2_)
+ theta2Source()
+ fvOptions(alpha, rho, theta2_)
);
PS: No, I have nothing to do with GRS, I am PhD student, working on SCWR. Thanks a lot so far! Last edited by Fabio1893; January 12, 2021 at 08:54. |
||
|
|

|
||
|
|
|
#4 |
|
New Member
Join Date: Jan 2021
Posts: 10
Rep Power: 5  |
I am still struggling with the algebraic equation. I wrote it as vector equation, but get a type error while compiling it, when I do it like this:
Code:
//Turbulen heat flux equation
tmp<fvVectorMatrix> thfEqn
(
thf_
==
- Ctu0_*(k()/epsilon())*(Ctu1_*this->sigma() & fvc::grad(T_)
+ Ctu2_*dev(twoSymm(fvc::grad(U))) & thf()
+ Ctu3_*beta_*theta2()*g)
+ Ctu4_*RSTanisotropy & thf()
);
Code:
volScalarField C = Ctu0_*(k()/epsilon());
volVectorField Term1 = C*Ctu1_*this->sigma() & fvc::grad(T_);
volVectorField Term2 = C*Ctu2_*dev(twoSymm(fvc::grad(U))) & thf();
volVectorField Term3 = C*Ctu3_*beta_*theta2()*g;
volVectorField Term4 = Ctu4_*RSTanisotropy & thf();
Code:
//Turbulent heat flux equation
tmp<fvVectorMatrix> thfEqn
(
thf_
==
- Term1
- Term2
- Term3
+ Term4
);
thfEqn.ref().relax();
fvOptions.constrain(thfEqn.ref());
solve(thfEqn);
Code:
error: invalid use of void expression 481 | tmp<fvVectorMatrix> thfEqn Last edited by Fabio1893; January 12, 2021 at 10:05. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
First to the problem of the algebraic equation.
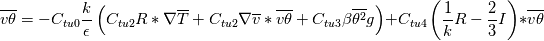 (3) (3)This is the algebraic equation. You have to rearrange it, so that the matrix equation is clear: 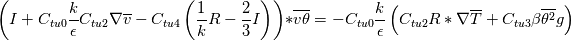 So the matrix A is everything before 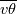 . It is of type volTensorField. So you can assign it to such a variable, e. g.: . It is of type volTensorField. So you can assign it to such a variable, e. g.:Code:
tmp<volTensorField> tgradU2 = fvc::grad(U_);
const volTensorField& gradU2 = tgradU2();
volTensorField leftSide
(
I
+ Ctu0_*k_/epsilon_*Ctu2_*gradU2
- Ct4_*...
);
Code:
volVectorField gradT(fvc::grad(T));
volVectorField rightSide
(
-Ctu0_*k_/epsilon_*
(
(Ctu2_*R & gradT)
+
(Ctu3_*beta_*g*thetaSqr_)
)
);
 : :Code:
thetaU_ = inv(leftSide) & rightSide; |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
Which solver will you use? Are you aware, that you have to modify the energy/temperature equation of the solver? Now the heat/energy flux becomes becomes a sum of the convective heat flux and the turbulent one, calculated by thetaU_. See e. g. equation 2 in https://www.researchgate.net/publica...PRANDTL_FLUIDS
|
|
|
|

|
|
|
|
|
#7 |
|
New Member
Join Date: Jan 2021
Posts: 10
Rep Power: 5  |
Thank you a lot again, the model compiles and runs now. - A first try, for now, without any use, since I do not use the thetaU yet. -
I use a slightly modified solver based on rhoSimpleFoam. I have added several fields in which I am interested and for simulation of mixed convection cases, I found that an additional buoyancy term in the momentum equation increases the simulation accuracy. For forced convection cases however, I use the "standard" momentum equation of rhoSimpleFoam. My idea was to redefine the calculation of the heat flux in the eddyDiffusivity.C, using thetaU, instead of changing the solvers energy equation. I think this will not make any difference at all, but maybe you have experience with that? I try to go both ways and will report it here, if someone is interested. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
I also added buoyancy terms to the turbulence equations. And for the other fields it is included in buoyantBoussineqPimpleFoam.
I made the experience that the simulations are unstable at the beginning and I had to use some tricks like limiting terms. When the simulations reached a steady state, these tricks were not longer needed. I think the problem is some terms on the right hand side of equation (4) are transport terms but do not have the "standard" form 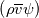 or or 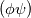 . . |
|
|
|

|
|
|
|
|
#9 |
|
New Member
Join Date: Jan 2021
Posts: 10
Rep Power: 5  |
I have also added buoyancy terms for k and epsilon, like this:
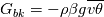 and 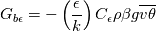 I have not implemented the last "step" yet, to use thetaU in the energy equation or in the eddy diffusivity model. Should be quite easy, but I did not find out yet, how to access the thetaU field from outside the library of the turbulence model. Anyway thanks for the hint with limiting terms. What boundary conditions do you use for the thetaSqr? |
|
|
|

|
|
|
|
|
#10 | |
|
Senior Member
Andrea
Join Date: Feb 2012
Location: Leeds, UK
Posts: 179
Rep Power: 16  |
Hi Joachim,
do you have any plans to release the source code of your implementation? Google translate is making a terrible job with your document  Regards, Andrea Quote:
|
||
|
|

|
||
|
|
|
#11 |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
Currently, the code is not really good enough to open source it. And it might get very complicated to get this aproved by the management.
But I might be able to answer specific implementation questions here. |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Andrea
Join Date: Feb 2012
Location: Leeds, UK
Posts: 179
Rep Power: 16  |
No problem, I fully understand your point.
BTW I have been working at NRG on this stuff for a while 
|
|
|
|

|
|
|
|
|
#13 | |
|
New Member
Join Date: Jan 2021
Posts: 10
Rep Power: 5  |
Quote:
Hi Joachim, since the energy equation is defined as fvScalarMatrix and thetaU_ is a volVectorField, I still can not finish my implementation. The same problem appears if I try to modify alphat in the eddyDiffusivity.C, which is a volScalarField. Can you give me any hint how to solve this problem? Best regards, Fabian |
||
|
|

|
||
|
|
|
#14 | |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
This is the energy equation you want to change?
https://github.com/OpenFOAM/OpenFOAM...oam/EEqn.H#L12 In the new form introduced in OpenFOAM-8 the diffusion is implemented in this divq method. You have to search for it. I am not sure, but is probably this implementation you need: https://github.com/OpenFOAM/OpenFOAM.../Fourier.C#L88 (only one fluid component) Here you see the use of the Reynolds analogy. Now you have to replace this term in the energy equation with the new diffusion term, e.g. the second summand on the right hand side of eq. (2) in https://www.researchgate.net/publica...PRANDTL_FLUIDS Quote:
|
||
|
|

|
||
|
|
|
#15 |
|
New Member
Join Date: Jan 2021
Posts: 10
Rep Power: 5  |
Hi Joachim,
yes, this energy equation is exactly the one I want to modify, with my changes marked in red. Code:
{
volScalarField& he = thermo.he();
volVectorField thetaU = U.db().objectRegistry::template lookupObject<volVectorField>("thetaU");
fvScalarMatrix EEqn
(
fvm::div(phi, he)
+ (
he.name() == "e"
? fvc::div(phi, volScalarField("Ekp", 0.5*magSqr(U) + p/rho))
: fvc::div(phi, volScalarField("K", 0.5*magSqr(U)))
)
//+ thermophysicalTransport->divq(he)
- rho*thermo.Cp()*fvc::div(thetaU)
==
fvOptions(rho, he)
);
EEqn.relax();
fvOptions.constrain(EEqn);
EEqn.solve();
fvOptions.correct(he);
thermo.correct();
}
Code:
template<class TurbulenceThermophysicalTransportModel>
tmp<fvScalarMatrix>
eddyDiffusivity<TurbulenceThermophysicalTransportModel>::divq
(
volScalarField& he
) const
{
return -fvm::laplacian(this->alpha()*this->alphaEff(), he);
}
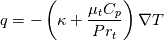 since in the algebraic model, the left part is still multiplied by the temperature gradient and the right part is something multiplied by thetaU (see eq (2)), I have to "split" this alpha()*alphaEff() part. Best regards, Fabian |
|
|
|

|
|
|
|
|
#16 |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
I acctually used buoyantBoussinesqPimpleFoam which has a temperature equation. So I could directly use equation (2).
https://github.com/OpenFOAM/OpenFOAM...pleFoam/TEqn.H There Code:
fvm::laplacian(alphaEff, T) Code:
fvm::laplacian(turbulence->nu()/Pr, T) + fvc::div(thetaU) |
|
|
|

|
|
|
|
|
#17 |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
Looking at equation (3) of https://www.sciencedirect.com/scienc...38573320309931
and considering, that https://github.com/OpenFOAM/OpenFOAM.../Fourier.C#L88 is just the laminar part the diffusion term should now be something like: Code:
fvm::laplacian(this->alpha()*this->thermo().alpha(), he) + rho*thermo.Cp()*fvc::div(thetaU) Edit: I think the first alpha is the phase fraction (because the model can also used for multi-phase simulations) and the second alpha (thermo().alpha()) is the thermal diffusivity. So for single phase flows, the first alpha = 1 Last edited by jherb; February 3, 2021 at 14:12. |
|
|
|

|
|
|
|
|
#18 |
|
New Member
Join Date: Jan 2021
Posts: 10
Rep Power: 5  |
Hi Joachim,
yes you are right, the first alpha is the phase fraction, this alpha appears also in all of the transport equations of the turbulence model. The second alpha, which is called alphaEff in the divq() function in my previous post, is, as you said, thermal diffusivity. We can find the definition in the heThermo.C file: Code:
template<class BasicThermo, class MixtureType>
Foam::tmp<Foam::volScalarField>
Foam::heThermo<BasicThermo, MixtureType>::alphaEff
(
const volScalarField& alphat
) const
{
return volScalarField::New
(
"alphaEff",
this->CpByCpv()*(this->alpha_ + alphat)
);
}
Code:
template<class TurbulenceThermophysicalTransportModel>
void eddyDiffusivity<TurbulenceThermophysicalTransportModel>::correctAlphat()
{
alphat_ =
this->momentumTransport().rho()
*this->momentumTransport().nut()/Prt_;
alphat_.correctBoundaryConditions();
}
Therefore, similar to your suggestion, I write the EEqn like this: Code:
fvScalarMatrix EEqn
(
fvm::div(phi, he)
+ (
he.name() == "e"
? fvc::div(phi, volScalarField("Ekp", 0.5*magSqr(U) + p/rho))
: fvc::div(phi, volScalarField("K", 0.5*magSqr(U)))
)
+ thermophysicalTransport->divq(he) - rho*thermo.Cp()*fvc::div(thetaU)
==
fvOptions(rho, he)
);
However, rho and Cp are definitely not constant over space, since I have strong variations in this properties with temperature close to the critical point and I have quite high spatial temperature gradients in my simulation cases. For now, the code is not running stable. I always get bounding thetaSqr, continuity errors explode after a while. Relaxation factors and numerical schemes have some influence, but I did not have a real success yet. I have tested the same case with the same turbulence model, without the additional transport equation and with the "standard" EEqn in the solver. Runs without any problem and results are what one would expect. Another point is, that the code only runs on a single core, but not in parallel. This seems to be due to the change in the energy equation. Best regards, Fabian |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
I think, this is not correct:
Code:
thermophysicalTransport->divq(he) - rho*thermo.Cp()*fvc::div(thetaU) Regarding the instabilities: This is exactly, what I saw. I think the problem might be related to the additional source terms in the different turbulence equations. Those terms are physically some kind of transport terms, but they are not in the form of fvc::div(phi, XXX). If they were one could use upstream schemes. But so, it looks like more of quantity of a cell is removed, compared to what is stored in the cell. |
|
|
|

|
|
|
|
|
#20 |
|
New Member
Join Date: Jan 2021
Posts: 10
Rep Power: 5  |
Yes you are right about that, since alphaEff is the molecular and the turbulent part together.
Therefore, I define a new function "divAlgebraic", which replaces the divq function in the EEqn of the solver. Instead of alphaEff, alphahe is used here, which is only the molecular part. Furthermore, I add the rho*Cp*div(thetaU) for the algebraic heat flux model, and also add the alpha for the phase fraction. Code:
template<class TurbulenceThermophysicalTransportModel>
tmp<fvScalarMatrix>
eddyDiffusivity<TurbulenceThermophysicalTransportModel>::divAlgebraic
(
volScalarField& he,
volVectorField& thetaU
) const
{
return -fvm::laplacian(this->alpha()*this->thermo().alphahe(), he) - this->alpha()*this->momentumTransport().rho()*this->thermo().Cp()*fvc::div(thetaU);
}
Code:
template<class BasicThermo, class MixtureType>
Foam::tmp<Foam::volScalarField>
Foam::heThermo<BasicThermo, MixtureType>::alphahe() const
{
return volScalarField::New
(
"alphahe",
this->CpByCpv()*this->alpha_
);
}
I think now the equations are correct, but still it is only possible to run on one single core, so there must be anything going wrong in the implementation. The biggest problem however, is the stability of the simulation. I understand your point about the form of the transport terms, but I dont know how to solve the issue. Can you tell me which divergence schemes you use? Best regads, Fabian |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Centrifugal fan-reverse flow in outlet lesds to a mass in flow field | xiexing | CFX | 3 | March 29, 2017 10:00 |
| Wrong flow in ratating domain problem | Sanyo | CFX | 17 | August 15, 2015 06:20 |
| CFX radiatin model wall heat flux imblance | cscfx | CFX | 0 | May 21, 2014 03:39 |
| UDF for Heat Exchanger model | francois louw | FLUENT | 2 | July 16, 2010 02:21 |
| Natural convection - Inlet boundary condition | max91 | CFX | 1 | July 29, 2008 20:28 |