[mcfdma]

Hi.

Rather than creating two threads, I am going to ask both my questions here since they are related.

I am using interFoam solver for my fluid flow simulation.

I am interested in acquiring the unit normal vector at the interface. I know the equation for normal vector is 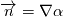which in OF can be written as

normV = fvc::grad(alpha1);

which compiles properly.

But when I try to compute the unit normal vector given by 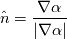which I have written using

unormV = fvc::grad(alpha1)/mag(fvc::grad(alpha1));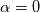

that also compiles properly. However, when running a case, my simulation crashes as the unit normal vector divides by 0 in the outer region where .

I am interested in acquiring unit normal vector to compute a variable which brings me to my second part of the question. The parameter I am measuring qs requires interface knowledge and is given by: .


My questions
1. How can I calculate unit normal vector 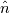at the interface?

2. How can I write the interface jump represented by ||.|| within my solver?

Any help is appreciated.

[gyr]

Did you solve the the problem,i am facing the same

[überschwupper]

I would do the calculation only for cells where the gradient isnt 0. That means, including an for loop where this condition is met

[gyr]

thanks so much