 |
|
|
[Sponsors] | |||||
Understanding temperature coupling BCs |
 53Likes
53Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 | |
|
Senior Member
Join Date: Oct 2013
Posts: 397
Rep Power: 18  |
I'm currently trying to understand the boundary conditions for temperature coupling between two regions, namely compressible::turbulentTemperatureCoupledBaffleMix ed and compressible::turbulentTemperatureRadCoupledMixed (source files located in turbulenceModels/compressible/turbulenceModel/derivedFvPatchFields/ ). In the first BC, radiation is neglected and the problem thus simplifies. In the .C file, one finds the following comment:
Quote:
I then assume that the gradient which is written here is only meant for the first side, and that the neighbour side is meant to be (temperature-nbrFld)*nbrDelta (possibly negative when the direction of the surface normal vector is considered). Now the two strategies below are meant to be used in iterative solvers I suppose. Does anyone know how the second one can be derived from the formulas? Or is it somewhat empirically determined to accelerate convergence maybe? For the second BC, things become more difficult because there are additional radiative heat fluxes, and no explaining comment. The strategy which is used here appears to be a bit different. The formulas used are: , where o=owner, n=neighbour, Delta=distance between cell center and patch face, kappa heat conductivity and Qr radiative heat flux. Does anyone understand this or has seen a derivative? I think this could be interesting for different heat transfer applications at boundaries. |
||
|
|

|
||
|
|
|
#2 |
|
Senior Member
Join Date: Oct 2013
Posts: 397
Rep Power: 18  |
I've spent some more time thinking about this. Using the equations above inserted into the mixed BC formula:
I'm wondering if the signs at the radiation fluxes are correct. For positive Q_r (meaning outgoing radiation) an iteration procedure using this formula is bound to diverge, because the sum of the two weighting factors in front of the temperatures is not 1??? As an example: Consider radiation coming out of a gas (0) being absorbed completely by a solid (1). In this case, Qr_0 > 0, Qr_1 = 0 and the sum of both factors is larger than 1. In my understanding this should result in an increasing temperature on each iteration. I'm going to test this series one dimensionally with MATLAB to investigate the convergence properties. Does anyone have any better explanation for the reasoning behind these formulas or maybe a literature recommendation? |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Oct 2013
Posts: 397
Rep Power: 18  |
See http://www.cfd-online.com/Forums/ope...tml#post517173 for further results.
|
|
|
|

|
|
|
|
|
#4 | |
|
Member
Atul Kumar
Join Date: Dec 2015
Location: National Centre for Combustion Research and Development
Posts: 48
Rep Power: 10  |
Quote:
HI Hi chriss Did you find a way to couple radiation of solid and gas phase. ???? |
||
|
|

|
||
|
|
|
#5 | ||
|
Member
Atul Kumar
Join Date: Dec 2015
Location: National Centre for Combustion Research and Development
Posts: 48
Rep Power: 10  |
Quote:
Quote:
Nice work Chriss |
|||
|
|

|
|||
|
|
|
#6 |
|
Senior Member
Join Date: Sep 2013
Posts: 353
Rep Power: 20  |
At the interface between fluid and solid (or solid and solid) the following is true:
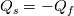 and and 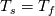 This means, that the heat flux exiting one domain enters the other and that both regions agree on temperature. The heat flux can be written as:  The gradient at the wall can be expressed as the difference between the value at the cell center and wall face devided by the distance between those. OpenFOAM uses the inverse of that however: 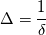 . . 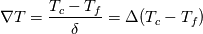 From here it is only a bit of math. We summarize the above condition: 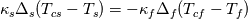 and simplify with 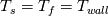 . This depends on the region you want to use the boundary condition for. For illustration we'll use the fluid side. . This depends on the region you want to use the boundary condition for. For illustration we'll use the fluid side.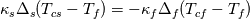 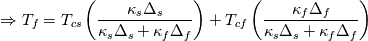 a mixed boundary condition in OpenFOAM is defined as follows: 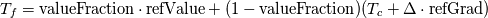 We can rewrite the above formula to match this: 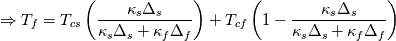 The actual implementation Code:
this->refValue() = nbrIntFld(); // This is T_s
this->refGrad() = 0.0;
this->valueFraction() = nbrKDelta()/(nbrKDelta() + myKDelta()); This is kappa*Delta
For adding in heat fluxes due to radiation you'd slightly modify the initial set up 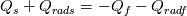 I have however not referenced this to the code. And am unsure about the sign of the radiation flux definition in OpenFOAM, so this might differ. It should however be a starting point for understanding the code. Last edited by Bloerb; November 27, 2018 at 03:05. |
|
|
|

|
|
|
|
|
#7 |
|
Member
Julian
Join Date: Sep 2019
Posts: 32
Rep Power: 6  |
Hi everyone, this is a very nice discussion. I am also working with this BC and am interested in a second-order formulation.
As written, the expression of flux continuity at the interface is 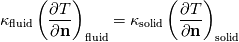 . .The derivatives are expanded via first-order differencing and the formulation is re-arranged for the interface temperature. Has anyone had success with a second-order BC for this? For example, replacing the temperature derivative with a second-order upwind type expression and re-arranging for interface temperature. This would require the two wall-adjacent cells which I suppose could be tricky to obtain. Thanks. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Uwe Pilz
Join Date: Feb 2017
Location: Leipzig, Germany
Posts: 744
Rep Power: 15  |
The case you described is not a boundary. Thee are inner faces with different values of kappa at both sides. The temperature simulation does not need anything more.
__________________
Uwe Pilz -- Die der Hauptbewegung überlagerte Schwankungsbewegung ist in ihren Einzelheiten so hoffnungslos kompliziert, daß ihre theoretische Berechnung aussichtslos erscheint. (Hermann Schlichting, 1950) |
|
|
|

|
|
|
|
|
#9 |
|
Member
Julian
Join Date: Sep 2019
Posts: 32
Rep Power: 6  |
Thank you for your input piu58.
I was examining boundary coupling and compared chtMultiRegionFoam with an analytical solution for semi-infinite media. A grid convergence study revealed the convergence was first-order despite using second-order spatial discretization, which motivated me to examine the coupling. The boundary condition is implemented and in fact hard-coded as a first-order scheme for interface temperature. |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
|
Dear Julian,
I fail to understand your post as much as I would like to. Are you sure that the scheme is only of first order only? How to you measure the order of the convergence? Are you sure that the order of convergence is not limited by first order schemes employed to discretize the convective terms in the equation? The reason for raising this doubt is the fact that my limited understanding tells me that the first order discretization used to discretize the fluid/solid interface conditions (local discretization error) should *not* lower the order of the volumetric scheme (global discretization error) from second to first order (for details see book of Piet Wesseling among others). Kind wishes, Domenico. |
|
|
|

|
|
|
|
|
#11 |
|
New Member
Eslam Reda
Join Date: Jun 2009
Posts: 19
Rep Power: 17  |
The full BC including a heat source (G) is expressed as: 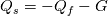 and and 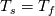 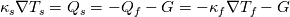 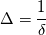 . . 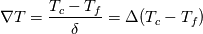 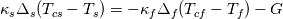 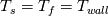 . .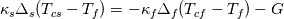 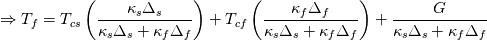 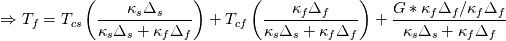  a mixed boundary condition in OpenFOAM is defined as follows (mixedFvPatchField.C): Field<Type>  perator= perator=( valueFraction_*refValue_ + (1.0 - valueFraction_) *( this->patchInternalField() + refGrad_/this->patch().deltaCoeffs() ) ); Hence, 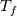 = Field<Type> = Field<Type> perator perator valueFraction_ = 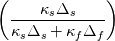 refValue_ = 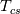 refGrad_ = 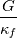 this->patch().deltaCoeffs() = 
|
|
|
|

|
|
|
|
|
#12 |
|
New Member
Join Date: Aug 2023
Posts: 1
Rep Power: 0  |
Do these formulation account for non-orthogonality of the face? If not, should they?
|
|
|
|

|
|
|
|
|
#13 | |
|
New Member
Join Date: Jun 2018
Posts: 20
Rep Power: 8  |
Quote:
Yes, deltaCoeffs includes a orthogonality correction. See https://openfoamwiki.net/index.php/O...n;;deltaCoeffs |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [openSmoke] libOpenSMOKE | Tobi | OpenFOAM Community Contributions | 562 | January 25, 2023 09:21 |
| Static Temperature / Opening Temperature | JulianP | CFX | 12 | April 10, 2019 18:00 |
| UDF for Back-flow Temperature | G340 | Fluent UDF and Scheme Programming | 3 | August 21, 2013 04:56 |
| Fluent Ansys temperature coupling | tensun | Fluent UDF and Scheme Programming | 0 | November 14, 2010 05:30 |
| high temperature in a coupling simulation | sheintz | STAR-CCM+ | 3 | September 30, 2010 13:56 |