 |
|
|
[Sponsors] | |||||
Solving coupled scalar transport equations in openFoam |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Pavan Inguva
Join Date: Dec 2019
Location: Singapore
Posts: 7
Rep Power: 6  |
Hi, I am trying to solve a series of coupled scalar transport equations i.e. temperature and chemical species transport for reacting flows by modifying icoFoam. I understand from a past forum post (quite a while ago) (How to solver coupled transport equations), that an iterative scheme is needed within openFoam.
If anyone could share what is the best practice for doing so, or if there a better way of solving these coupled equations, that would be immensely helpful. The model equations are as follows: 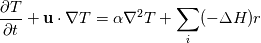 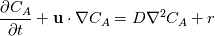 where  is given by a standard arrhenius expression which couples the two transport equations.: is given by a standard arrhenius expression which couples the two transport equations.: 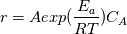 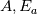 are the preexponential factor and activation energy and are the preexponential factor and activation energy and 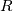 is the ideal gas constant. is the ideal gas constant.I intend to solve this part outside the PISO loop as the temperature and chemical species do not strongly affect flow and can be neglected. But I am not too sure how to couple these two equations within openFoam. I understand that the following implementation provides a 1 way coupling of the velocity to the temperature equation: ``` // --- PISO loop while (piso.correct()) { volScalarField rAU(1.0/UEqn.A()); volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p)); surfaceScalarField phiHbyA ( "phiHbyA", fvc::flux(HbyA) + fvc::interpolate(rAU)*fvc::ddtCorr(U, phi) ); adjustPhi(phiHbyA, U, p); // Update the pressure BCs to ensure flux consistency constrainPressure(p, U, phiHbyA, rAU); // Non-orthogonal pressure corrector loop while (piso.correctNonOrthogonal()) { // Pressure corrector fvScalarMatrix pEqn ( fvm::laplacian(rAU, p) == fvc::div(phiHbyA) ); pEqn.setReference(pRefCell, pRefValue); pEqn.solve(); if (piso.finalNonOrthogonalIter()) { phi = phiHbyA - pEqn.flux(); } } #include "continuityErrs.H" U = HbyA - rAU*fvc::grad(p); U.correctBoundaryConditions(); } // This is where we add the temperature transport equations: fvScalarMatrix TEqn ( fvm:: ddt(T) // The phi bit is a function argument which represents a vol<Type>Field + fvm:: div(phi, T) - fvm:: laplacian(alpha, T) // We need to add the source term below here: ); TEqn.solve(); ``` Thanks for your help! |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Michael Alletto
Join Date: Jun 2018
Location: Bremen
Posts: 615
Rep Power: 16  |
There are at least two option you can follow:
1) use a segregated approach: you first solve for T using the values of CA of the old time step and than you solve for CA using the newly computed values of T. I do not how good this will work because the equation for CA is very stiff. But this is implemented quit easily 2) Use the same method as above but apply an operator splitting method for CA: First solve the ordinary differential equation 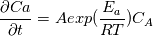 . Use the averaged value over the time step of CA computed by solving the differential equation to compute the reaction rate and solve the partial differential equation for CA. This method is used in the solver of openfaom involving chemical reactions like chemFoam, reactingFoam ore fireFaom. . Use the averaged value over the time step of CA computed by solving the differential equation to compute the reaction rate and solve the partial differential equation for CA. This method is used in the solver of openfaom involving chemical reactions like chemFoam, reactingFoam ore fireFaom.Best Michael |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Free surface issues with interDyMFoam for hydroturbine | oumnion | OpenFOAM Running, Solving & CFD | 0 | October 6, 2017 14:05 |
| compressible flow in turbocharger | riesotto | OpenFOAM | 50 | May 26, 2014 01:47 |
| calculation stops after few time steps | sivakumar | OpenFOAM Running, Solving & CFD | 7 | March 17, 2013 06:37 |
| Orifice Plate with a fully developed flow - Problems with convergence | jonmec | OpenFOAM Running, Solving & CFD | 3 | July 28, 2011 05:24 |
| Could anybody help me see this error and give help | liugx212 | OpenFOAM Running, Solving & CFD | 3 | January 4, 2006 18:07 |