[Chris T]

Hi everyone.

My question might sound silly. I can't tell if my simulation is solving the compressible or incompresible Navier-Stokes equations. I'm using the chtMultiregionFoam solver I have a molten salt (liquid) region, air (gas) region and some solid regions. I based my simulation on another simulation on a similar system.
Though the velocities involved in the simulation are very low and by themselves they don't excuse the use of the compressible equations I do have a temperature dependent density (using rhoCoeffs<8>) in both fluid regions to accurately account for buoyancy.

Based on the discussion here [GUIDE] Switching from incompressible to compressible simulation I'm assuming the way I have my simulation set up is compressible due to the fact that the dimensions in my p file are [ 1 -1 -2 0 0 0 0 ].
Also after reading some of the theory I would also assume that I have to use the the compressible equations because even though my fluids act approximately as compressible my density is a function of temperature which in turn is a function of coordinates in space and time which will make it to not commute with derivative operators.

1) Is my assessment correct regarding the use of the compressible form of the equations in my case?
2) In Openfoam v9 what signals to the solver to use which version of the equation? Is changing the dimensions of p and having a T and alphat files enough? What else am I missing?
3) Is the Pr number calculated by the solver automatically? I am not specifying it at the moment.



Best,
Chris

[Tobermory]

1) Yes. Your problem is "weakly compressible", i.e. low Mach number, and so free of shocks ... but with variable density, and pressure, density and temperature related by your EoS (probably perfectGas?). You could probably revert the problem back to an incompressible case, using a Boussinesq approximation for the temperature effects, but that would mean a different solver, and there's probably no need.

2) This is determined within the solver - it's not runtime selectable. How to tell? The simplest way is to just look at UEqn.H and see whether this includes density - compare for example pisoFoam (https://cpp.openfoam.org/v10/incompr...8H_source.html) with your solver (https://cpp.openfoam.org/v10/heatTra...8H_source.html).

3) Now this is not obvious! I am assuming that you are running with the sutherland viscosity model? If so, then on line 128 of sutherlandTransport.H (https://cpp.openfoam.org/v9/sutherla...8H_source.html) you'll see a definition of the thermal conductivity, kappa, based on the Eucken correlation:

 template<class Thermo>
 inline Foam::scalar Foam::sutherlandTransport<Thermo>::kappa
 (
     const scalar p,
     const scalar T
 ) const
 {
     scalar Cv_ = this->Cv(p, T);
     return mu(p, T)*Cv_*(1.32 + 1.77*this->R()/Cv_);
 }

This, along with the Sutherland correlation for viscosity, effectively sets the laminar Prandtl number for the simulation:



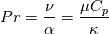Hope the above helps.

[Bloerb]

Basically in chtMultiRegion the thermoPhysicalProperties define your equation of state. Just write type banana or some error like that and run the solver to get the full list of all the options available.

thermoType
{
    type              heRhoThermo;
    mixture         pureMixture;
    transport       const;
    thermo          hConst;
    equationOfState perfectGas;
    specie           specie;
    energy          sensibleInternalEnergy;
}

So equationOfState "rhoConst" would mean incompressible for example. perfectGas and others are different forms of compressibility. The solver itself does however always use p [ 1 -1 -2 0 0 0 0 ] and not like all the other incompressible solvers p*=p/rho. This is because you can run an incompressible simulation but use temperature dependend properties, like the viscosity etc. The form of the energy equation (h or e) is specified with sensibleInternalEnergy or sensibleEnthalpy. "Sensible" means no phase change in this context. So the equations solved are basically always the same. Aside from the energy variable h/e and even that is just a numerical choice with marginal influence on your results. It is how the density is updated in that equation that gives you the compressibility or not.

If you solve with turbulence alphat will be added. If you need to specify the Pr number or kappa, viscosity or a set of coefficients etc, depends on the thermo and transport settings above. For hConst for example you need to specify Pr and the solver calculates the thermal diffusivity it needs for the equation from that using the other specified constants. For hPolynomial you need to specify kappa directly.


So the equations solved are basically modular in openfoam. alpha for example in the code is just a place holder and depends on what settings you used above. For sensibleEnthalpy it is kappa/cp and for sensibleEnergy kappa/cv. The DivDevReff term in UEqn for example switches between different formulations depending on whether you use turbulence or not.

[Chris T]

Dear Tobermory and Bloerb

Thank you for your useful replies. Now I know what I'm actually doing rather than guessing what might be the case regarding the equations that are solved.

To put all new information I got from your posts in single sentences:
- [ 1 -1 -2 0 0 0 0 ] are always the p dimensions in chtMyltiregionFoam.
- In chtMyltiregionFoam, the U equation contains rho unlike other solvers that are only used in incompressible cases.
- The thermoPhysicalProperties/thermoType/equationOfState entry determines the "compresibility" of equations with rhoConst the only option for "fully" incompressible equations.


Some followup comments/questions:
- I vagely remember from a tutorial that the Boussinesq approximation for the temperature effects is only valid for small ΔT but in my simulation my max T and my min T differ by ~300 K.
- in my case I use icoPolynomial for both air and molten salt regions. Of courde with different parameters. The one bellow is for air. I now understand that in my case the incompressible Navier-Stokes equation are solved but with temperature varying parameters.

thermoType
{
    type            heRhoThermo;
    mixture         pureMixture;
    transport       polynomial;
    thermo          hPolynomial;
    equationOfState icoPolynomial;
    specie          specie;
    energy          sensibleEnthalpy;
}

mixture
{
    specie
    {
       nMoles          1;        
       molWeight       28.89;        // [g/mol]
    }
    equationOfState
    {
       rhoCoeffs<8>   (2.6083 -7.2239e-03 9.2920e-06 -5.6049e-09 1.2797e-12 0 0 0); // Valid from 300 K to 1500 K
    }
    thermodynamics
    {
        CpCoeffs<8>   (1061.3 4.3282e-1 1.0234e-3 -6.4747e-7 1.3864e-10 0 0 0); // [J/(Kg K)]
        Hf              0;
        Sf              0;
    }
    transport
    {
        kappaCoeffs<8>  (-7.488e-3 1.7082e-4 -2.3758e-7 2.2012e-10 9.46e-14 1.5797e-17 0 0); // [W/m/K]
        muCoeffs<8>     (4.113e-6 5.0523e-8 -1.4346e-11 2.5914e-15 0 0 0 0); // [Kg/(m s) = (N s)/m^2 = Pa s]
        //Pr = (mu Cp)/k
    }
}

- how does one chooses viscosity models (sutherland or other)? in addition to the above thermopysicalProperties my momentumTransport is

simulationType  RAS;

RAS
{
    RASModel        kOmegaSST;
    turbulence      on;
    printCoeffs     on;
 }

Best,
Chris

[Tobermory]

For your third point:

The thermoPhysicalProperties/thermoType/equationOfState entry determines the "compresibility" of equations with rhoConst the only option for "fully" incompressible equations.

I think that I would state it slightly differently. The equations are the same, whether the flow is compressible or not; the main thing is the approach that you take in solving them efficiently - and that's tied up in the coding of the solver. chtMultiregionFoam is always a weakly compressible solver, even if it is running with a rhoConst EOS. It can handle incompressible flows just fine, as Bloerb points out, esp. if you use a rhoConst EOS, but it will struggle with strongly compressible flows, regardless of the EOS you use. Regardless, this is just semantics - I think you are clear on what you're doing.

On the Boussinesq question - yes, absolutely right. It is only useful if 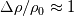, which typically means small .

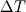And finally, on the viscosity models - this is specified by the transport keyword in the thermoPhysicalProperties file - check out: https://doc.cfd.direct/openfoam/user...36-2720007.1.2. The Sutherland model is used for gases. Check out some of the chtMultiRegionFoam tutorials for examples (eg cd to the tutorials folder and type "grep -r transport heatTransfer/chtMultiRegionFoam" and you'll see which tutorials use what).

[Chris T]

Dear Tobermory

Thanks again for your response. Could you please elaborate on what you mean by "weakly compressible". I'm trying to understand what that implies for the equations solved. I also try to find some analogy with the theory I'm reading up right now.
When deriving the Navier-Stokes equation one can derive the full set of equation with minimal assumptions just from conservation principles and that way get the compressible version of the equations. Then take the comprehensibility assumption 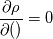and derive the incompressible set of equation.
How does "weakly compressible" compressible fit into this framework?


Sorry if my question doesn't make sense an/or is too difficult.


Chris

[Tobermory]

Chris - it does make sense. A key thing to keep in mind is that the NS equations behave very differently at different Mach numbers.

At the Ma=0 limit, we have incompressible conditions, and pressure information travels instantaneously throughout the domain. For Ma > 1, we have supersonic flow, and the transmission of information is limited in direction. For 0 < Ma <= ~0.3 we have conditions that are approximately incompressible, i.e. pressure perturbations in the flow generate negligible perturbations in density, and can often be ignored without any serious loss in accuracy. This is the regime that I was calling "weakly compressible". For 0.3 < Ma < 1 then compressibility effects are significant, and density varies strongly with pressure; pressure information is moving through the domain at the speed of sound.

These different behaviours mean that different solution methods are either required, or are at least far more efficient, for each regime. If you want to read up a bit more, google on elliptic, parabolic and hyperbolic equations ... but be prepared to read a lot! This YT video might help, albeit it's fairly dry (https://www.youtube.com/watch?v=DroQ...P0Xqk&index=55).

Good luck!

[Chris T]

Thanks again for your reply and for the resources.


Also above I meant question not equation but you got the point.