 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
S Abrahams
Join Date: Mar 2022
Location: UK
Posts: 14
Rep Power: 4  |
Hi everyone!
I wonder if anyone can help me to understand the formulation of the TEqn in compressibleInterFoam in OF9. The TEqn is: Code:
fvm::ddt(rho, T) + fvm::div(rhoPhi, T) - fvm::Sp(contErr, T)
- fvm::laplacian(turbulence.alphaEff(), T)
+ (
fvc::div(fvc::absolute(phi, U), p)()() // - contErr/rho*p
+ (fvc::ddt(rho, K) + fvc::div(rhoPhi, K))()()
- (U()&(fvModels.source(rho, U)&U)()) - contErr*K
)
*(
alpha1()/mixture.thermo1().Cv()()
+ alpha2()/mixture.thermo2().Cv()()
)
==
fvModels.source(rho, T)
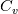 should be inside the derivatives since should be inside the derivatives since 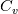 is averaged over the two phases and can therefore vary in time and space. is averaged over the two phases and can therefore vary in time and space. I believe the TEqn should be equivalent to 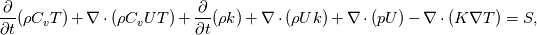 but the formulation above seems to be equivalent to ![\frac{C_{1}C_{2}}{{\alpha_1 C_{2}+\alpha_2 C_{1}}} \left[\frac{\partial}{\partial t}(\rho T)+\nabla\cdot(\rho U T) \right]+ \frac{\partial}{\partial t}(\rho k)+\nabla\cdot(\rho U k)+\nabla \cdot (pU)-\nabla\cdot (K \nabla T)=S. \frac{C_{1}C_{2}}{{\alpha_1 C_{2}+\alpha_2 C_{1}}} \left[\frac{\partial}{\partial t}(\rho T)+\nabla\cdot(\rho U T) \right]+ \frac{\partial}{\partial t}(\rho k)+\nabla\cdot(\rho U k)+\nabla \cdot (pU)-\nabla\cdot (K \nabla T)=S.](/Forums/vbLatex/img/dcab439af1722422590c7a7e283f4419-1.gif) Can anyone help me to understand how 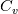 has been taken out in this way? has been taken out in this way?Many thanks, SAbrahams 
Last edited by sabrahams; August 9, 2023 at 13:09. Reason: typos |
|
|
|

|
|
|
|
|
#2 |
|
New Member
S Abrahams
Join Date: Mar 2022
Location: UK
Posts: 14
Rep Power: 4  |
Does no-one know the answer to this?
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
I think the problem lies with your first Teqn equation ... Start from basics - the underlying energy equation is stated in terms of the internal energy, i.e. in conservative form:
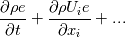 which we can expand out using continuity to the non-conservative form: 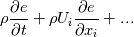 Now using the definition of the specific heat, we write 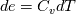 , so substitute and you have: , so substitute and you have: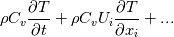 or in terms of the material derivative: 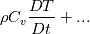 with the specific heat capacity on the outside. Hopefully that helps. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
S Abrahams
Join Date: Mar 2022
Location: UK
Posts: 14
Rep Power: 4  |
Hi Tobermory,
Thanks for your reply. However, since 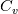 is not a constant in this case, I don't believe we can say is not a constant in this case, I don't believe we can say 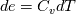 . Instead, it should be . Instead, it should be 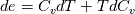 . .In a two phase system, as we have in compressibleInterFoam, 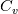 is averaged over the two phases, that is is averaged over the two phases, that is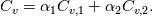 While 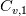 and and 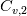 may be constant, may be constant, 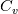 is not since is not since 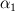 and and 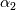 vary in time and space. vary in time and space. Furthermore, TEqn in compressibleInterFoam (as shown in my original post) is not 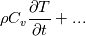 it seems to be (if you divide through by 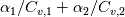 , which is multiplying the second term in TEqn) , which is multiplying the second term in TEqn)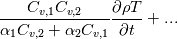 So I'm trying to understand how the energy equation has been rearranged to get the form in the TEqn as in my original post. Do you know how this is derived? Thanks again, SAbrahams Last edited by sabrahams; August 15, 2023 at 11:28. Reason: correcting mistake in equation |
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
Okay - let me break this down. First up, the following is not correct I am afraid:
Quote:
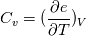 ... and now can you see where I got my original ... and now can you see where I got my original 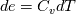 from? We have said nothing so far about the variability of Cv in space, just that the process is assumed to be a constant volume process (which makes sense for two immiscible fluids). If you're still not convinced, then think of the chain rule: from? We have said nothing so far about the variability of Cv in space, just that the process is assumed to be a constant volume process (which makes sense for two immiscible fluids). If you're still not convinced, then think of the chain rule: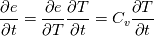 etc. Now consider the single phase energy equation, which in OpenFOAM is (refer to buoyantPimpleFoam for example): 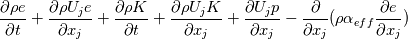 expand out the first two terms into the nonconservative form using continuity, substitute for 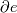 and convert back to conservative form and you get: and convert back to conservative form and you get:![\frac{\partial \rho T}{\partial t} + \frac{\partial \rho U_j T}{\partial x_j} +
\frac{1}{C_v}[\frac{\partial \rho K}{\partial t} + \frac{\partial \rho U_j K}{\partial x_j} + \frac{\partial U_j p}{\partial x_j}]
- \frac{1}{C_v}\frac{\partial}{\partial x_j}(\rho C_v \alpha_{eff} \frac{\partial T}{\partial x_j}) \frac{\partial \rho T}{\partial t} + \frac{\partial \rho U_j T}{\partial x_j} +
\frac{1}{C_v}[\frac{\partial \rho K}{\partial t} + \frac{\partial \rho U_j K}{\partial x_j} + \frac{\partial U_j p}{\partial x_j}]
- \frac{1}{C_v}\frac{\partial}{\partial x_j}(\rho C_v \alpha_{eff} \frac{\partial T}{\partial x_j})](/Forums/vbLatex/img/e8d1e6af333b45b7be553c0b2bbb8e9a-1.gif) NOW a minor approximation is made in the laplacian, where it assumed that local variations in Cv are small, so that the terms cancel leaving: ![\frac{\partial \rho T}{\partial t} + \frac{\partial \rho U_j T}{\partial x_j} +
\frac{1}{C_v}[\frac{\partial \rho K}{\partial t} + \frac{\partial \rho U_j K}{\partial x_j} + \frac{\partial U_j p}{\partial x_j}]
- \frac{\partial}{\partial x_j}(\rho \alpha_{eff} \frac{\partial T}{\partial x_j}) \frac{\partial \rho T}{\partial t} + \frac{\partial \rho U_j T}{\partial x_j} +
\frac{1}{C_v}[\frac{\partial \rho K}{\partial t} + \frac{\partial \rho U_j K}{\partial x_j} + \frac{\partial U_j p}{\partial x_j}]
- \frac{\partial}{\partial x_j}(\rho \alpha_{eff} \frac{\partial T}{\partial x_j})](/Forums/vbLatex/img/2e400455114b664b8899fe68ea49c804-1.gif) and we are almost there. All that is left is to realise that the finite volume discretised form of the energy (or temperature) budget equation is the sum of alpha1 times the equation for phase 1 plus alpha2 times that for phase two, which results in: ![(\alpha_1 + \alpha_2)[\frac{\partial \rho T}{\partial t} + \frac{\partial \rho U_j T}{\partial x_j}] (\alpha_1 + \alpha_2)[\frac{\partial \rho T}{\partial t} + \frac{\partial \rho U_j T}{\partial x_j}]](/Forums/vbLatex/img/65c8c43bd9bd88dcf0c825bc6ebff041-1.gif) ![+ (\frac{\alpha_1}{C_{v1}}+\frac{\alpha_2}{C_{v2}})[\frac{\partial \rho K}{\partial t} + \frac{\partial \rho U_j K}{\partial x_j} + \frac{\partial U_j p}{\partial x_j}]
- (\alpha_1 + \alpha_2)\frac{\partial}{\partial x_j}(\rho \alpha_{eff} \frac{\partial T}{\partial x_j}) + (\frac{\alpha_1}{C_{v1}}+\frac{\alpha_2}{C_{v2}})[\frac{\partial \rho K}{\partial t} + \frac{\partial \rho U_j K}{\partial x_j} + \frac{\partial U_j p}{\partial x_j}]
- (\alpha_1 + \alpha_2)\frac{\partial}{\partial x_j}(\rho \alpha_{eff} \frac{\partial T}{\partial x_j})](/Forums/vbLatex/img/ffe67ae29068c76eea3e9aa0a5a3a07e-1.gif) or on noting that 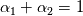 , we have: , we have:![\frac{\partial \rho T}{\partial t} + \frac{\partial \rho U_j T}{\partial x_j} +
(\frac{\alpha_1}{C_{v1}}+\frac{\alpha_2}{C_{v2}})[\frac{\partial \rho K}{\partial t} + \frac{\partial \rho U_j K}{\partial x_j} + \frac{\partial U_j p}{\partial x_j}]
- \frac{\partial}{\partial x_j}(\rho \alpha_{eff} \frac{\partial T}{\partial x_j}) \frac{\partial \rho T}{\partial t} + \frac{\partial \rho U_j T}{\partial x_j} +
(\frac{\alpha_1}{C_{v1}}+\frac{\alpha_2}{C_{v2}})[\frac{\partial \rho K}{\partial t} + \frac{\partial \rho U_j K}{\partial x_j} + \frac{\partial U_j p}{\partial x_j}]
- \frac{\partial}{\partial x_j}(\rho \alpha_{eff} \frac{\partial T}{\partial x_j})](/Forums/vbLatex/img/fa4bef4634e3fdc047f7976330b5fe88-1.gif) noting that these should now not be differentials etc., but should instead be volume integrals of the differentials yielding volume average values or surface fluxes (I didn't have the time to tidy up the terminology). This is the form that appears in TEqn.h for compressibleInterFoam. There are clearly a bunch of other implicit assumptions here ... but this is my reverse engineering of the code. I couldn't find any explicit reference to the source of the model equations, and suspect it was authored by one of the OpenFOAM team. If you do find a reference - share it with the forum please. Last edited by Tobermory; August 16, 2023 at 12:36. |
||
|
|

|
||
|
|
|
#6 |
|
New Member
S Abrahams
Join Date: Mar 2022
Location: UK
Posts: 14
Rep Power: 4  |
That makes perfect sense. Thank you for the clear explanation!
I haven't found any references for the equations used in compressibleInterFoam in OF9. If I find anything I'll certainly share. UEqn and alphaEqn appear to be in the same form as equations (7) and (25) of Shi et al.. Although, this paper was published later than OF9 so isn't a reference but just a useful resource to understand the equations (for anyone else reading this). Thanks again Tobermory. |
|
|
|

|
|
|
|
|
#7 | |
|
New Member
S Abrahams
Join Date: Mar 2022
Location: UK
Posts: 14
Rep Power: 4  |
Hi again Tobermory,
I've just been working through this and I'm stuck on this step: Quote:
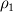 and the equation for phase 2 would have and the equation for phase 2 would have 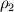 so I'm struggling to see how the two equations could be summed in the way that you've shown above. I'm getting an equation of the form: so I'm struggling to see how the two equations could be summed in the way that you've shown above. I'm getting an equation of the form:![\alpha_1 [\frac{\partial \rho_1 T}{\partial t} + \frac{\partial \rho_1 U_j T}{\partial x_j}] \alpha_1 [\frac{\partial \rho_1 T}{\partial t} + \frac{\partial \rho_1 U_j T}{\partial x_j}]](/Forums/vbLatex/img/f2ef78f4dc84584dc09f6ba817332e0c-1.gif) ![+
\alpha_2[\frac{\partial \rho_2 T}{\partial t} + \frac{\partial \rho_2 U_j T}{\partial x_j}] + ... +
\alpha_2[\frac{\partial \rho_2 T}{\partial t} + \frac{\partial \rho_2 U_j T}{\partial x_j}] + ...](/Forums/vbLatex/img/c7874a59900f91884e290cbc8c10adc8-1.gif) Am I missing a step or an assumption somewhere? |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
The way to think of it, I reckon, is as follows: we need to integrate the differential equations over the cell volume to get the finite volume expressions. Focus just on the first two terms, for simplicity:
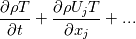 integrate these to get: 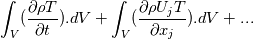 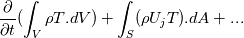 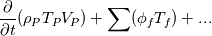 where it's assumed that the mesh is not moving or morphing, 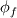 are the face fluxes, and the P subscript denotes a volume-averaged value, e.g. are the face fluxes, and the P subscript denotes a volume-averaged value, e.g.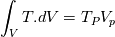 Note though that we are integrating over volume 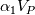 for phase 1, and for phase 1, and 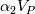 for phase 2. This is the origin of the for phase 2. This is the origin of the 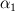 and and 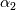 coefficients in each of the terms. This is what I meant rather laconically in my earlier post by "noting that these should now not be differentials etc.". Hope this helps. coefficients in each of the terms. This is what I meant rather laconically in my earlier post by "noting that these should now not be differentials etc.". Hope this helps.
|
|
|
|

|
|
 |
| Tags |
| heat capacity, temperature, teqn |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Correction of T after TEqn in compressibleInterFoam | krikre | OpenFOAM Programming & Development | 3 | June 26, 2022 22:07 |
| TEqn (passive scalar) diverges all of a sudden | backscatter | OpenFOAM Running, Solving & CFD | 11 | October 21, 2018 07:56 |
| TEqn. in PorousSimpleFoam | svramana | Main CFD Forum | 0 | February 14, 2018 08:53 |
| EEqn to TEqn | jishnuhari25 | OpenFOAM Programming & Development | 1 | June 4, 2015 11:06 |
| Replace H equation with Teqn in chtMultiregionFoam OF 2.3 | Moncef | OpenFOAM Running, Solving & CFD | 0 | May 22, 2014 20:37 |