 |
|
|
[Sponsors] | |||||
|
|
|
#21 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
You are correct. The deviatoric tensor is traceless but as you see out of the derivation this term will remain. I did more derivations and put all together. I think I am going to share this with you. Also divDevRhoReff and divDevReff are included.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#22 |
|
Senior Member
Agustín Villa
Join Date: Apr 2013
Location: Alcorcón
Posts: 314
Rep Power: 15  |
Quote:
In the OpenFOAM programmer's guide, it is said that: dev (A) = A - 1/3 * trace(A) * I So I think the bold part I quoted is not correct at all: the other term should be removed instead the one you used, if I am not wrong. At the end, since it is an incompressible case, it should not be a problem during your derivation. |
|
|
|

|
|
|
|
|
#23 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Again,
you are right. The deviatoric part is tracefree but I also added the trace because it is a term of numerical stabilisation. This will happen due to the fact of my derivation. Also you are right that the deviatoric part of a matrix is defined as: 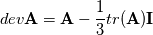 But you mix up the way I derived the equation. Starting from the incompressible term; that means that the conti is zero and also the secondary viscosity 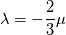 is zero it follows for the shear-rate tensor: is zero it follows for the shear-rate tensor:![\boldsymbol \tau = [\nu \nabla \textbf{U} + \nu(\nabla \textbf{U})^T] \boldsymbol \tau = [\nu \nabla \textbf{U} + \nu(\nabla \textbf{U})^T]](/Forums/vbLatex/img/16ea2ef4e53c6da26c14af8ea7280056-1.gif) to be more consistent it would be actually: ![\boldsymbol \tau = [\nu \nabla \otimes \textbf{U} + \nu(\nabla \otimes \textbf{U})^T] \boldsymbol \tau = [\nu \nabla \otimes \textbf{U} + \nu(\nabla \otimes \textbf{U})^T]](/Forums/vbLatex/img/6a7c3aa665211e8e2d67a5ca1a5a70cd-1.gif) What I was doing now was adding the trace of gradient U and removed it again: ![\boldsymbol \tau = [\nu \nabla \otimes \textbf{U} + \nu(\nabla \otimes \textbf{U})^T + \nu \frac{1}{3} tr (\nabla \textbf{U}) \textbf{I} - \nu \frac{1}{3} tr (\nabla \textbf{U}) \textbf{I} ] \boldsymbol \tau = [\nu \nabla \otimes \textbf{U} + \nu(\nabla \otimes \textbf{U})^T + \nu \frac{1}{3} tr (\nabla \textbf{U}) \textbf{I} - \nu \frac{1}{3} tr (\nabla \textbf{U}) \textbf{I} ]](/Forums/vbLatex/img/8989206a98fa16655de5784327490ab1-1.gif) It also can be shown that:  which is actually the continuity equation which is zero for incompressible fluids. I think so far we are fine. Due to the fact that the terms of 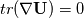 we remove the last term and keep the first one. That results in the euqation I showed you above. we remove the last term and keep the first one. That results in the euqation I showed you above. Now you can also do it vice versa. Then you will end up with the negative trace which will actually lead to the defintion of the deviatoric part. So it's only a sign question we are talking about at the moment. Due to the fact that the trace term has no influence if you are converged, we can neglect it. We can feel free to add or remove it. Of course if we consider the deviatoric definition we will at least end up with the negative trace; this derivation I also did in the paper/summary I will publish. AND of course it has a more physical way to use the negative trace because it is at least the definition of the deviatoric part (: Also I am not sure if the solution will change if we would add the trace part. At least to clean everything up. I should have used the negative trace in my derivation, because then we get the same stuff as in the FOAM code and we correspond with the definition of the deviatoric part. I hope it is clear now! The only thing that is wrong at the above equations is that the sign of the trace if you start from the deviatoric definition is different. Then you get a minus sign at the trace. BUT again this part can also be neglected due to the continuity equation and one may implement it without the trace. This term is only kept for numerical stabilization.
__________________
Keep foaming, Tobias Holzmann Last edited by Tobi; December 3, 2015 at 09:20. Reason: Added identity matrix |
|
|
|

|
|
|
|
|
#24 |
|
New Member
Nikolai Tauber
Join Date: Sep 2015
Location: Aarhus, Denmark
Posts: 14
Rep Power: 10  |
Hi,
I have been trying to figure out the exact implementation of incompressible RANS equation based on this thread and this article http://openfoamwiki.net/index.php/Bu...sinesqPisoFoam Nevertheless, there are a few things I do not understand, and i think there are a few mistakes in the article. Anyway, I will start by showing you my derivation from RANS to OpenFOAM: __________________________________________________ ____________ The incompressible RANS equation is given by, ![u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho}\frac{\partial p}{\partial x_i}+\frac{\partial}{\partial x_j}\left[\nu\left(\frac{\partial u_i}{\partial x_j }+\frac{\partial u_j}{\partial x_i}\right)-\overline{u'_iu'_j} \right] u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho}\frac{\partial p}{\partial x_i}+\frac{\partial}{\partial x_j}\left[\nu\left(\frac{\partial u_i}{\partial x_j }+\frac{\partial u_j}{\partial x_i}\right)-\overline{u'_iu'_j} \right]](/Forums/vbLatex/img/43f6c579cd4d5c7b1d851725dfe7f887-1.gif) where the Boussinesq approximation states: 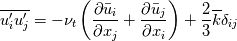 Expressing the Reynolds stresses with the Boussinesq approximation gives cause for, ![\bar{u}_j\frac{\partial\bar{u}_i}{\partial\bar{u}_j} =-\frac{1}{\rho}\frac{\partial p}{\partial x_i} + \frac{\partial}{\partial x_j} \left[(\nu+\nu_{t}) \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right)\delta_{ij} -\frac{2}{3}k \delta_{ij}\right] \bar{u}_j\frac{\partial\bar{u}_i}{\partial\bar{u}_j} =-\frac{1}{\rho}\frac{\partial p}{\partial x_i} + \frac{\partial}{\partial x_j} \left[(\nu+\nu_{t}) \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right)\delta_{ij} -\frac{2}{3}k \delta_{ij}\right]](/Forums/vbLatex/img/b6eb72de9dc049d6830b10d2e6a679bf-1.gif) where the kinetic energy term, 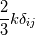 , drops out. , drops out.What would seem to pose a paradox in connection with the incompressibility assumption is introduced. The isotropic part of the stress tensor is added and subtracted again. This entails:  Due to incompressibility the positive isotropic part of the stress tensor can be canceled and an expansion of the equation gives rise to: 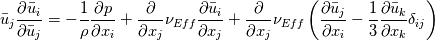 This is the incompressible turbulent RANS equation for fluids where  and thus and thus 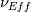 cannot be taken outside the spatial derivative due to it being a variable as a consequence of large temperature variations (or other reasons e.g. non-newtonian). cannot be taken outside the spatial derivative due to it being a variable as a consequence of large temperature variations (or other reasons e.g. non-newtonian).In OpenFOAM the terms can be identified as, 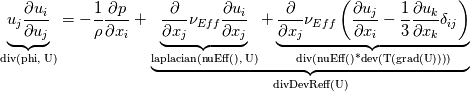 which exactly what is given in the source code of the momentum equation, Code:
tmp<fvVectorMatrix> UEqn
(
fvm::div(phi, U)
+ turbulence->divDevReff(U)
);
Code:
tmp<fvVectorMatrix> kOmegaSST::divDevReff(volVectorField& U) const
{
return
(
- fvm::laplacian(nuEff(), U)
- fvc::div(nuEff()*dev(T(fvc::grad(U))))
);
}
Code:
inline Tensor<Cmpt> dev(const Tensor<Cmpt>& t)
{
return t - SphericalTensor<Cmpt>::oneThirdI*tr(t);
}
My questions: - Why does the kinematic energy term drop out? Is it because the gradient of it is very small? - Why is the isotropic part of the stress tensor added and subtracted again when it is zero due to incompressibility? So it is for numerical reasons, but which numerical reasons? |
|
|
|

|
|
|
|
|
#25 | |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Quote:
The reason is the following: - I don't know it exactly without having a look into the code but it is easy to understand - You have an estimation of the velocity field and hence you know the fluxes - Then you calculate the pressure field due to the fluxes. Then you get new fluxes due to a new velocity field. - NOW: for incompressible fluids 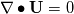 but will never be exactly zero due to numerics (imagine abort error) but will never be exactly zero due to numerics (imagine abort error) - Therefore this term is not zero especially at the beginning of a calculation - If we use this term we introduce somehow "additional flux" which then will lead to faster convergence Till now I did not check your derivation but your kinetmatic energy term seems to be the secondary viscosity or first lames coefficient that is zero for incompressible fluids. You should start really from the beginning with the Cauchy stress tensor and start to derive the Navier-Stokes equations without any averaging and turbulence models. If you do so you get: 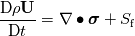 where the last term represents other sources like buoyancy, gravitational acceleration and so on (neglecting now). Then we know that we can split the Cauchy stress tensor to a hydrostatic and deviatoric part. At least the hydrostatic part is the negative pressure and the deviatoric part is for Newtonian fluids the shear rate tensor 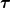 . We get: . We get: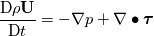 It can be derived that the deviatoric part is actually: ![\boldsymbol \tau = 2 \mu \underbrace{\frac{1}{2} [ \nabla \otimes \textbf{U} + (\nabla \otimes \textbf{U})^T}_{\mathrm{tensor~} \textbf{D}}] + \left\{(\lambda + \kappa) \nabla \bullet \textbf{U}\right\} \textbf{I} \boldsymbol \tau = 2 \mu \underbrace{\frac{1}{2} [ \nabla \otimes \textbf{U} + (\nabla \otimes \textbf{U})^T}_{\mathrm{tensor~} \textbf{D}}] + \left\{(\lambda + \kappa) \nabla \bullet \textbf{U}\right\} \textbf{I}](/Forums/vbLatex/img/ea1ce9766993159d6c06a61a4bc41f16-1.gif) D is also known as deformation rate tensor. Here we have the gradients of Velocity. If we are in solid mechanics, we get the gradient of displacements. The last term is due to compression and expansion effects.  is named bulk viscosity that is zero for low gases and almost neglect able for dense gases and liquids. At least we end up with that equation: is named bulk viscosity that is zero for low gases and almost neglect able for dense gases and liquids. At least we end up with that equation: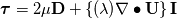 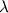 is the first Lamés coefficient, also known as secondary viscosity which is actually for Newtonian fluids is the first Lamés coefficient, also known as secondary viscosity which is actually for Newtonian fluids 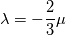 . If we are in solid mechanics we have to replace . If we are in solid mechanics we have to replace 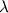 with other equations. We end up: with other equations. We end up: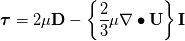 that is actually the same like: 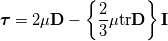 Now for incompressible fluids, the secondary viscosity is zero (no expansion and compression), also the divergence of velocity is zero (continuity). Therefore the last term is removed. If we also introduce the assumption of constant viscosity we will end up with a simple formulation for the shear-rate tensor and at least (laplace equation), if the shear-rate tensor is zero we get the famous Euler equation. Now if we introduce some turbulence models, nothing will be changed in the shear rate tensor. Only the viscosity will increase due to the fact that that the assumption of the common turbulence models are based on the increase of viscosity. Therefore I don't get the point why you have 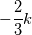 in your equation. in your equation.
__________________
Keep foaming, Tobias Holzmann |
||
|
|

|
||
|
|
|
#26 |
|
New Member
Nikolai Tauber
Join Date: Sep 2015
Location: Aarhus, Denmark
Posts: 14
Rep Power: 10  |
Hi Tobias,
Thank you for your thorough answer. As I understand, you suggest that I have mixed up turbulent kinematic energy and bulk viscosity. I do not think that is the case. According to this reference http://www.cfd-online.com/Wiki/Bouss...ity_assumption The Boussinesq eddy assumption includes mean turbulent kinetic energy, and it has nothing to do with bulk viscosity. I still do not understand why the mean turbulence kinetic energy drops out. For consistency, I have now included the basics of the derivation from Cauchy's equation of motion to the implementation of the RANS kOmegaSST turbulence model in OpenFOAM: ---------------------------------------------------------------------------------------- Cauchy's equation of motion states:  It relates the fluid-particle acceleration to the net body force (here just from gravity),  , and the surface force, , and the surface force, 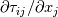 . The stress tensor, . The stress tensor, 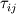 , is composed of a deviatoric part, , is composed of a deviatoric part,  , for viscous shear stresses and an isotropic part, , for viscous shear stresses and an isotropic part, 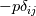 , for fluid static normal stresses: , for fluid static normal stresses: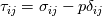 The viscous shear stress tensor is given by, ![\sigma_{ij}=\left[2\mu S_{ij}+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\right] \sigma_{ij}=\left[2\mu S_{ij}+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\right]](/Forums/vbLatex/img/b96eab66a4938836e37b0e26ec3f78df-1.gif) and the strain-rate is: 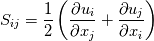 Combining everything produces the NS in its full form: ![\rho\bigg(\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial u_j}\bigg)=-\frac{\partial p}{\partial x_i}+\rho g_i+\frac{\partial}{\partial x_j}\bigg[\mu\bigg(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\bigg)+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\bigg] \rho\bigg(\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial u_j}\bigg)=-\frac{\partial p}{\partial x_i}+\rho g_i+\frac{\partial}{\partial x_j}\bigg[\mu\bigg(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\bigg)+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\bigg]](/Forums/vbLatex/img/3541e785f3731d72d24fb3a959346fe1-1.gif) Assuming incompressibility, steady state and neglecting gravity gives rise to:  Reynolds decomposition,  produces the RANS equation which is given by: ![u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_i}+\frac{\partial}{\partial x_j}\left[\nu\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)-\overline{u'_iu'_j} \right] u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_i}+\frac{\partial}{\partial x_j}\left[\nu\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)-\overline{u'_iu'_j} \right]](/Forums/vbLatex/img/9832decdd27fe6d4780227e8dc6ddd93-1.gif) According to http://www.cfd-online.com/Wiki/Bouss...ity_assumption ,with the notation from the reference, the Boussinesq approximation for an incompressible flow states: 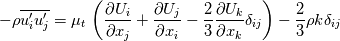 For an incompressible flow it is thus: 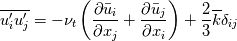 Expressing the Reynolds stresses with the Boussinesq approximation gives cause for, ![\bar{u}_j\frac{\partial\bar{u}_i}{\partial\bar{u}_j} =-\frac{1}{\rho}\frac{\partial p}{\partial x_i} + \frac{\partial}{\partial x_j} \left[(\nu+\nu_{t}) \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right) -\frac{2}{3}k \delta_{ij}\right] \bar{u}_j\frac{\partial\bar{u}_i}{\partial\bar{u}_j} =-\frac{1}{\rho}\frac{\partial p}{\partial x_i} + \frac{\partial}{\partial x_j} \left[(\nu+\nu_{t}) \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right) -\frac{2}{3}k \delta_{ij}\right]](/Forums/vbLatex/img/8ba3ddd457c73e066af8c943c1b28f93-1.gif) where the kinetic energy term, 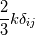 , drops out. , drops out.What would seem to pose a paradox in connection with the incompressibility assumption is introduced. The isotropic part of the stress tensor is added and subtracted again. This entails:  Due to incompressibility the negative isotropic part of the stress tensor can be canceled and an expansion of the equation gives rise to: 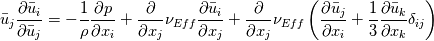 This is the incompressible turbulent RANS equation for fluids where  and thus and thus 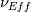 cannot be taken outside the spatial derivative due to it being a variable as a consequence of large temperature variations (or other reasons e.g. non-newtonian). cannot be taken outside the spatial derivative due to it being a variable as a consequence of large temperature variations (or other reasons e.g. non-newtonian).In OpenFOAM the terms can be identified as, 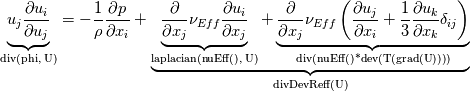 which exactly what is given in the source code of the momentum equation, Code:
tmp<fvVectorMatrix> UEqn
(
fvm::div(phi, U)
+ turbulence->divDevReff(U)
);
Code:
tmp<fvVectorMatrix> kOmegaSST::divDevReff(volVectorField& U) const
{
return
(
- fvm::laplacian(nuEff(), U)
- fvc::div(nuEff()*dev(T(fvc::grad(U))))
);
}
Code:
inline Tensor<Cmpt> dev(const Tensor<Cmpt>& t)
{
return t - SphericalTensor<Cmpt>::oneThirdI*tr(t);
}
|
|
|
|

|
|
|
|
|
#27 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hi,
okay as far as I read your equations your are right but it is interesting that everybody denotes everything with other symbols. In all literature that I read, the Cauchy stress tensor is denoted by  and the deviatoric part of this tensor (the shear-rate tensor) as and the deviatoric part of this tensor (the shear-rate tensor) as 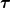 . In your case it is exactly vice versa. Anyway ... . In your case it is exactly vice versa. Anyway ...I just wanted to mention this for people who are not so familiar with the equations (if someone will read all the stuff)  Okay. Your derivation seems to be well done and I also found in my literature also the definition / approximation: 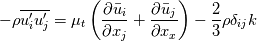 But as far as I know the equations we get the following: The Navier-Stokes-Equation with the Reynolds-Average method is given as: 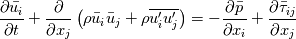 Up to know I think we are at the same level. The stress-tensor 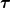 is calculated as before... the only difference is that we take the mean value of the velocity and the effective viscosity. Therefore the calculation of the U field is okay for the shear-rate tensor. is calculated as before... the only difference is that we take the mean value of the velocity and the effective viscosity. Therefore the calculation of the U field is okay for the shear-rate tensor. Now if we check out the equation above and compare it with yours, we get the same but in your equation the fluctuation term is put to the right hand side and is combined with the stress tensor. I think so far we are fine. The question now is, what happen to the term including the kinetic energy. Till now I dont know but I will check it out. Maybe I am not correct but if I insert everything into the reynolds averaged equation we get: LHS: 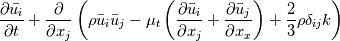 RHS: ![=
- \frac{\partial \bar p}{\partial x_i} + \frac{\partial}{\partial x_j} \underbrace{\left[\mu_t \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_x}\right) - \frac{2}{3}\mu_t \frac{\partial u_k}{\partial x_k} \delta_{ij} \right]}_{\mathrm{shear-rate~tensor}} =
- \frac{\partial \bar p}{\partial x_i} + \frac{\partial}{\partial x_j} \underbrace{\left[\mu_t \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_x}\right) - \frac{2}{3}\mu_t \frac{\partial u_k}{\partial x_k} \delta_{ij} \right]}_{\mathrm{shear-rate~tensor}}](/Forums/vbLatex/img/1f384665fb2e391d6fec4ef737c3e85d-1.gif) Then we can make some simple math to get at least your eqaution that is side sth like (RHS): ![\frac{\partial}{\partial x_i} \left[2 \mu_t \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_x}\right)\right] + \frac{\partial}{\partial x_i} \left(-\frac{2}{3}\mu_t \frac{\partial u_k}{\partial x_k} \delta_{ij} - \frac{2}{3}k \delta_{ij}\right) \frac{\partial}{\partial x_i} \left[2 \mu_t \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_x}\right)\right] + \frac{\partial}{\partial x_i} \left(-\frac{2}{3}\mu_t \frac{\partial u_k}{\partial x_k} \delta_{ij} - \frac{2}{3}k \delta_{ij}\right)](/Forums/vbLatex/img/a4cc2c8496a3dcfb2321db0ca46e26f6-1.gif) I think you agree with me. If the second term is zero we actually get the implementation of icoFoam with the factor 2. Of course it is clear what will happen if we have incompressible flow. But what will happen with the term that include k, I don't know. But as we can see, in the calculation of the deviatoric part of the stress tensor there is no twoSymm(grad(U)) included and I think the terms that appear (its the first one in this post) is treated somewhere else. Maybe in the pressure equation somehow? But I hope I could show you the way that the shear-rate tensor calculation (laplacian->turbulence...) has no influence of the reynolds averaging (RHS) At least I would mention that you should use the turbulence viscosity for the shear-rate tensor (you used the laminar viscosity).
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#28 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hi,
I talked to my college and he told me that this term with k is not included (buoyancy turbulent) because it is so small and can be neglected.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#29 |
|
New Member
Nikolai Tauber
Join Date: Sep 2015
Location: Aarhus, Denmark
Posts: 14
Rep Power: 10  |
Hi,
Thanks! I expected k to be small and negligible. Correct me if I am wrong, but I do not think you are right in connection with the viscosity. The RANS equation expressed with the Boussinesq approximation should include the sum of the molecular (laminar) viscosity  and the turbulent eddy viscosity and the turbulent eddy viscosity 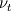 i.e. i.e. 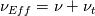 . Like this: . Like this:![\frac{\partial}{\partial x_j} \left[(\nu+\nu_{t}) \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right)\right] \frac{\partial}{\partial x_j} \left[(\nu+\nu_{t}) \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right)\right]](/Forums/vbLatex/img/71a89908293a8258136b83c96146d4c1-1.gif) In your derivation (where I have allowed myself to correct what I suppose is simply a misspelling): ![\frac{\partial}{\partial x_i} \left[2 \mu_t \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right)\right] \frac{\partial}{\partial x_i} \left[2 \mu_t \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right)\right]](/Forums/vbLatex/img/2a4c09e760dd4f0f46a0b9023ac329b4-1.gif) you only have the turbulent eddy viscosity. That does not make sense to me, as diffusion would not be present in laminar regimes of a flow problem. Also 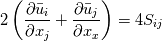 does not make sense, as it equals four times the strain rate instead of only two. Check the Cauchy's equation again. |
|
|
|

|
|
|
|
|
#30 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hi,
Of course you are right. In terms of buoyancy turbulence you should use the effective viscosity. How you get 4 x S? In my previous derivatives it would be better to use the effective viscosity instead of the turbulent. That is obvious. Unfortunately I am not available till Wednesday. But I will replay after I read my books
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#31 |
|
New Member
Nikolai Tauber
Join Date: Sep 2015
Location: Aarhus, Denmark
Posts: 14
Rep Power: 10  |
Hi,
The viscous shear stress tensor (the one I call  and you call and you call 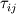 ) is given by, ) is given by,![\sigma_{ij}=\left[2\mu S_{ij}+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\right] \sigma_{ij}=\left[2\mu S_{ij}+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\right]](/Forums/vbLatex/img/b96eab66a4938836e37b0e26ec3f78df-1.gif) and the strain rate: 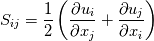 Combining, ![\sigma_{ij}=\left[2\mu \frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\right] \sigma_{ij}=\left[2\mu \frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\right]](/Forums/vbLatex/img/a041dcfbcf175b1632aebf4aadebd4c8-1.gif) produces: ![\sigma_{ij}=\left[\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\right] \sigma_{ij}=\left[\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)+\bigg(\mu_v-\frac{2}{3}\mu\bigg)\frac{\partial u_k}{\partial x_k}\delta_{ij}\right]](/Forums/vbLatex/img/996a80e662a1a7f33a0a67b46b28871f-1.gif) You thus need to omit the 2 in this: ![\frac{\partial}{\partial x_i} \left[2 \mu \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right)\right] \frac{\partial}{\partial x_i} \left[2 \mu \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i}\right)\right]](/Forums/vbLatex/img/b424579f874ee1c0108c6e5f21215950-1.gif) Just to be clear, for the above everything is laminar. About the turbulent viscosity: I do not see why using the effective velocity is only necessary for buoyancy turbulence. The effective viscosity should always be used, right? |
|
|
|

|
|
|
|
|
#32 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hi Niko,
thanks for the replay but I know how the equations look like (: You are right that the number "2" is shortened with the 1/2 from the strain-rate tensor. For the 2 in my derivation I have to check. Maybe I will do it today. For the viscosity. The best way is to use the effective viscosity but sometimes you will find that people only use the turbulent viscosity. For example, I used the flamelet model build by Alberto Cuoci et. al. in my masterthesis. This model is based on high turbulence and therefore laminar effects are really neglectible and they only used turbulence->mu(). However I prefer to use the effective viscosity.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#33 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear Nico,
you are right. I made a mistake with the viscosities  . .Here are my derivation that I did now... I have to check it again these days but it seems that everything is correct.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#34 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hi all,
I checked the derivation yesterday again and there should be a mistake with the sign. I will check it again today. Regards, Tobi
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#35 |
|
New Member
chariton christou
Join Date: Feb 2014
Posts: 26
Rep Power: 12  |
Hi All,
I am trying to implement a new stress tensor for compressible flows. instead of divDevRhoReff(U) i am trying to do: volVectorField UK("UK", U*10); and change the stress tensor to divDevRhoReff(UK) I just want to test how the simulation will react for higher velocity. I also tried the volTensorField tauMC("tauMC", muEff*dev2(Foam::T(fvc::grad(UK)))); and my simulation crash as well. Does anyone knows why it happens for high values of the velocity? Thank you in advance |
|
|
|

|
|
|
|
|
#36 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Niko I have a question to you:
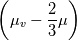 The first term in your equation is the volumetric viscosity also known as bulk viscosity that is neglected in most/all equations (Bird et. al). I ask because in solid mechanics we have the deviatoric part of the stress tensor given by: 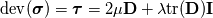 If we talk about a newtonian fluid we have: 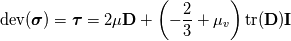 Now I am not sure if I can say that: 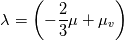 or maybe: 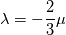 And the bulk viscosity is zero for solids. I read that 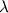 is also known as dilitational viscosity or in solid mechanics first Lámes coefficent. If its so, I think the second one is valid. Hope you get the point. is also known as dilitational viscosity or in solid mechanics first Lámes coefficent. If its so, I think the second one is valid. Hope you get the point. Again... I am asking if we can generalize the shear-rate tensor (for solids and fluids) as: 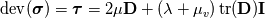 where 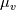 is zero for solids and neglectable for fluids and is zero for solids and neglectable for fluids and 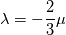 if we talk about netwonian fluids or is it even better or are we allowed to define it like: if we talk about netwonian fluids or is it even better or are we allowed to define it like: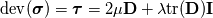 where 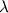 is defined for newtonian liquids as: is defined for newtonian liquids as: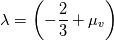 Hope it is clear (: @charitonas: If you think about conservation of equations you make a big mistake!
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#37 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Hi all,
now the derivation are done clearly and smooth: http://www.cfd-online.com/Forums/ope...tml#post580452
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#38 |
|
Senior Member
Gerhard Holzinger
Join Date: Feb 2012
Location: Austria
Posts: 340
Rep Power: 28   |
||
|
|

|
|
|
|
|
#39 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Thanks for the interesting hint. That means that we calculate p' in OpenFOAM? Well I have to check it out in the literature.
Good to know. So at least the term exist in FOAM?
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#40 |
|
Senior Member
Gerhard Holzinger
Join Date: Feb 2012
Location: Austria
Posts: 340
Rep Power: 28   |
We are solving for all kinds of stuff.
If you apply Reynolds-averaging to your governing equations and apply the Boussinesq hypothesis, then you solve for the Reynolds averaged flow quantities. The pressure is the sum of the actual, Reynolds averaged pressure and the isotropic part of the Reynolds stress tensor. The actual pressure is also the isotropic part of a general fluid stress tensor. However, for probably historical reasons, we separate the pressure and the (shear) stresses. In solid mechanics there is no such distinction, at least up to the point I got in contact with solid mechanics and FE simulation. If you apply spatial filtering to derive the governing equations with LES turbulence modelling, then you end up with equations for the grid-scale flow quantities. The sub-grid stress tensor in LES modelling is analogous to the Reynolds stress tensor in RANS modelling. Also in LES modelling, the pressure you solve for is the sum of the actual pressure and the isotropic part of the sub-grid stress tensor. The beauty of this derivations is, although, we get equations for different things (temporal or spatially filtered flow quantities), the equations have the same mathematical structure. This allows the makers of CFD simulation software to implement a generic handling of turbulence. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Calculating Vorticity | David | CFX | 28 | October 29, 2017 18:02 |
| Calculating Drag | Ajay Rao | FLUENT | 8 | February 15, 2010 09:15 |
| what is Fluent calculating? | tomek | FLUENT | 1 | July 24, 2006 17:52 |
| errors in calculating | ustcer | FLUENT | 1 | April 4, 2004 13:08 |
| Calculating Coefficients | shabah | CFX | 2 | June 18, 2001 23:59 |