2-D vortex in isentropic flow
From CFD-Wiki
Roberthealy1 (Talk | contribs) m (I think that this article may qualify as a stub, as it represents a POV; "one choice". An explanation of what the test is and what it can be used for would be worthwhile) |
(Fixed mistake in pressure as pointed out by Kevin Schaal.) |
||
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
| - | The test case involves [[convection]] of an [[isentropic]] [[vortex]] in [[inviscid flow]]. | + | This is one of the few exact solutions for the compressible Euler equations. The test case involves [[convection]] of an [[isentropic]] [[vortex]] in [[inviscid flow]]. It is used to show the ability of numerical schemes to accurately capture vortical flows. The [[free-stream conditions]] are |
| - | The [[free-stream conditions]] are | + | |
:<math> | :<math> | ||
\begin{matrix} | \begin{matrix} | ||
\rho &=& 1 \\ | \rho &=& 1 \\ | ||
| - | u &=& | + | u &=& u_\infty \\ |
| - | v &=& | + | v &=& v_\infty \\ |
| - | p &=& 1 | + | p &=& 1 |
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
Perturbations are added to the [[free-stream]] in such a way that there is no | Perturbations are added to the [[free-stream]] in such a way that there is no | ||
| - | [[entropy]] gradient in the [[flow-field]]. The perturbations are given by | + | [[entropy]] gradient in the [[flow-field]]. The perturbations in the velocity are given by: |
| - | + | <math> | |
| + | (\delta u, \delta v) = \frac{\beta}{2\pi} \exp\left( \frac{1-r^2}{2} | ||
| + | \right) [ -(y-y_o), (x-x_o) ] | ||
| + | </math> | ||
| + | |||
| + | while the temperature, density and pressure are given by | ||
| + | |||
| + | <math> | ||
\begin{matrix} | \begin{matrix} | ||
| - | + | T &=& 1 - \frac{ (\gamma-1)\beta^2}{8\gamma\pi^2} \exp\left( | |
| - | + | 1-r^2\right)\\ | |
| - | + | \rho &=& T^{\frac{1}{\gamma-1}} \\ | |
| - | 1-r^2\right) \ | + | p &=& \rho T = \rho^\gamma |
| - | p &=& \ | + | |
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
| Line 41: | Line 46: | ||
As a result of [[isentropy]], the exact solution corresponds to a pure [[advection]] | As a result of [[isentropy]], the exact solution corresponds to a pure [[advection]] | ||
| - | of the [[vortex]] at the [[free-stream velocity]]. Further details can be found in Yee et al. (1999). | + | of the [[vortex]] at the [[free-stream velocity]]. This problem is usually solved with periodic boundary conditions. Further details can be found in Yee et al. (1999). |
==References== | ==References== | ||
Latest revision as of 04:00, 21 October 2014
This is one of the few exact solutions for the compressible Euler equations. The test case involves convection of an isentropic vortex in inviscid flow. It is used to show the ability of numerical schemes to accurately capture vortical flows. The free-stream conditions are
Perturbations are added to the free-stream in such a way that there is no entropy gradient in the flow-field. The perturbations in the velocity are given by:
![(\delta u, \delta v) = \frac{\beta}{2\pi} \exp\left( \frac{1-r^2}{2}
\right) [ -(y-y_o), (x-x_o) ]](/W/images/math/b/f/4/bf4d03266bdcc72a5731401a2efc95dc.png)
while the temperature, density and pressure are given by
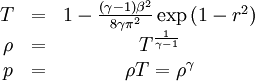
where
is distance from the vortex center 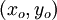 .
.
One choice for the domain and parameters is:
As a result of isentropy, the exact solution corresponds to a pure advection of the vortex at the free-stream velocity. This problem is usually solved with periodic boundary conditions. Further details can be found in Yee et al. (1999).
References
- Yee, H-C., Sandham, N. and Djomehri, M., (1999), "Low dissipative high order shock-capturing methods using characteristic-based filters", JCP, Vol. 150.

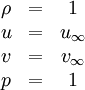
![r = [ (x-x_o)^2 + (y-y_o)^2 ]^{1/2}](/W/images/math/6/3/5/635b76a00e794bbe4119341445847905.png)
![\Omega = [0,10] \times [-5,5], \quad
(x_o, y_o) = (5,0), \quad
\beta = 5](/W/images/math/c/e/a/ceae1619f8ff0db839e9a7afecbd5f9c.png)