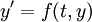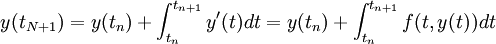Adams methods
From CFD-Wiki
(Difference between revisions)
(corrected equation) |
Roberthealy1 (Talk | contribs) (What are BDF Methods?) |
||
| Line 1: | Line 1: | ||
| - | Adams' methods are a subset of the family of | + | == Introduction == |
| + | |||
| + | Adams' methods are a subset of the family of [[multi-step methods]] used for the [[numerical integration]] of initial value problems in [[Ordinary Differential Equations]] (ODE's). [[Multi-step methods]] benefit from the fact that the computations have been going on for some time, and use previously computed values of the solution (BDF methods), or the right hand side (Adams' methods), to approximate the solution at the next step. | ||
Adams' methods begin by the integral approach, | Adams' methods begin by the integral approach, | ||
| Line 12: | Line 14: | ||
</math> | </math> | ||
| - | Since <math>f</math> is unknown in the interval <math>t_n</math> to <math>t_{n+1}</math> it is approximated by an interpolating [[polynomial]] <math>p(t)</math> using the previously computed steps <math>t_{n},t_{n-1},t_{n-2} ...</math> and the current step at <math>t_{n+1}</math> if an implicit method is desired. | + | Since <math>f</math> is unknown in the interval <math>t_n</math> to <math>t_{n+1}</math> it is approximated by an [[interpolating]] [[polynomial]] <math>p(t)</math> using the previously computed steps <math>t_{n},t_{n-1},t_{n-2} ...</math> and the current step at <math>t_{n+1}</math> if an implicit method is desired.{{fact}} |
| + | |||
| + | == References == | ||
| + | |||
| + | ? | ||
| + | |||
| + | {{stub}} | ||
Latest revision as of 18:53, 13 August 2007
Introduction
Adams' methods are a subset of the family of multi-step methods used for the numerical integration of initial value problems in Ordinary Differential Equations (ODE's). Multi-step methods benefit from the fact that the computations have been going on for some time, and use previously computed values of the solution (BDF methods), or the right hand side (Adams' methods), to approximate the solution at the next step.
Adams' methods begin by the integral approach,
Since 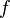 is unknown in the interval
is unknown in the interval 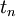 to
to 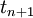 it is approximated by an interpolating polynomial
it is approximated by an interpolating polynomial 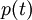 using the previously computed steps
using the previously computed steps 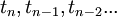 and the current step at
and the current step at 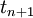 if an implicit method is desired.
if an implicit method is desired.
References
?