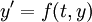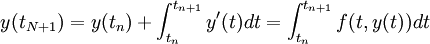Adams methods
From CFD-Wiki
Revision as of 00:01, 10 December 2005 by Discoganya (Talk | contribs)
Adams methods are a subset of the general family of multistep methods used for the numerical integration of initial value problems based on odes. Multistep methods benefit from the fact that the computation has been going on for a while and use previously computed values of the solution (BDF methods) or the right hand side (Adams methods) to approximate the solution at the next step.
Adams methods begin by the integral approach,
Since 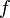 is unknown in the interval
is unknown in the interval 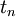 to
to 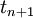 it is approximated by an interpolating polynomial
it is approximated by an interpolating polynomial 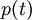 using the previously computed steps
using the previously computed steps 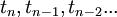 and the current step at
and the current step at 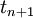 if an implicit method is desired.
if an implicit method is desired.