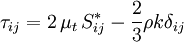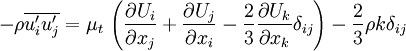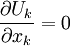Boussinesq eddy viscosity assumption
From CFD-Wiki
| Line 3: | Line 3: | ||
:<math>\tau_{ij} = 2 \, \mu_t \, S_{ij}^* - \frac{2}{3} \rho k \delta_{ij}</math> | :<math>\tau_{ij} = 2 \, \mu_t \, S_{ij}^* - \frac{2}{3} \rho k \delta_{ij}</math> | ||
| - | Where <math>\mu_t</math> is a scalar property called the [[Eddy viscosity|eddy viscosity]]. The same | + | Where <math>\mu_t</math> is a scalar property called the [[Eddy viscosity|eddy viscosity]]. The same equation can be written more explicitly as: |
:<math> -\rho \overline{u'_i u'_j} = \mu_t \, \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} - \frac{2}{3} \frac{\partial U_k}{\partial x_k} \delta_{ij} \right) - \frac{2}{3} \rho k \delta_{ij}</math> | :<math> -\rho \overline{u'_i u'_j} = \mu_t \, \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} - \frac{2}{3} \frac{\partial U_k}{\partial x_k} \delta_{ij} \right) - \frac{2}{3} \rho k \delta_{ij}</math> | ||
Revision as of 14:54, 7 April 2011
In 1877 Boussinesq postulated that the momentum transfer caused by turbulent eddies can be modeled with an eddy viscosity. This is in analogy with how the momentum transfer caused by the molecular motion in a gas can be described by a molecular viscosity. The Boussinesq assumption states that the Reynolds stress tensor, 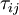 , is proportional to the trace-less mean strain rate tensor,
, is proportional to the trace-less mean strain rate tensor, 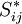 , and can be written in the following way:
, and can be written in the following way:
Where 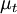 is a scalar property called the eddy viscosity. The same equation can be written more explicitly as:
is a scalar property called the eddy viscosity. The same equation can be written more explicitly as:
Note that for incompressible flow:
The Boussinesq eddy viscosity assumption is also often called the Boussinesq hypothesis or the Boussinesq approximation.
References
Boussinesq, J. (1877), "Essai sur la théorie des eaux courantes", Mémoires présentés par divers savants à l'Académie des Sciences XXIII, 1, pp. 1-680.
Schmitt, F.G. (2007), "About Boussinesq’s turbulent viscosity hypothesis: historical remarks and a direct evaluation of its validity", Comptes Rendus Mécanique, vol. 335 (9-10), pp. 617-627; doi:10.1016/j.crme.2007.08.004.