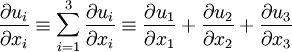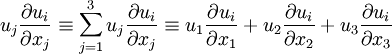Einstein summation convention
From CFD-Wiki
(Difference between revisions)
TrocoUcacn (Talk | contribs) (lisitlilit) |
m (Reverted edits by TrocoUcacn (Talk) to last version by Jola) |
||
| Line 1: | Line 1: | ||
| - | |||
The Einstein summation convention is a tensor notation which is commonly used to implicitly define a sum. The convention states that when an index is repeated in a term that implies a sum over all possible values for that index. | The Einstein summation convention is a tensor notation which is commonly used to implicitly define a sum. The convention states that when an index is repeated in a term that implies a sum over all possible values for that index. | ||
Latest revision as of 09:52, 17 December 2008
The Einstein summation convention is a tensor notation which is commonly used to implicitly define a sum. The convention states that when an index is repeated in a term that implies a sum over all possible values for that index.
Here are two examples: