Flow around a circular cylinder
From CFD-Wiki
Contents |
Introduction
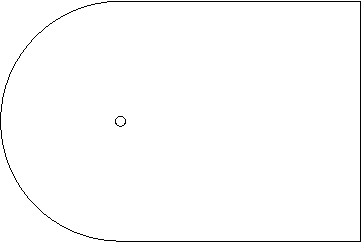
The flow around a (geometrically) two-dimensional circular cylinder is case that has been used both as a validation case and as a legitimate research case. At very low Reynolds numbers, the flow is steady and symmetrical. As the Reynolds number is increased, asymmetries and time-dependence develop, eventually resulting the famous Von Karmann vortex street, and then on to turbulence. The problem geometry is two-dimensional and there is some variation in the details (both geometry and boundary conditions) that can be used. A typical geometry is shown below (not to scale).
The exterior boundaries are generally placed very far from the cylinder surface to avoid interaction between the boundary conditions. Grid generation is not especially difficult, though care must be taken to properly resolve the near-wall region as the Reynolds number is increased.
This problem has been solved as both a laminar flow and a turbulent flow. The DNS, LES, and the transitional cases are still considered a research cases. Many different numerical techniques have been used to solve this problem, but one usual comparison is the the resulting Strouhal frequency (if the simulation is in the proper Reynolds number range.
Many variations on the geometry are possible. One can impose symmetry by cutting the solution domain in half (along the x-direction). This will reduce the computational burden, but will reduce the range of physical applicability of the simulations (asymmetries develop at rather moderate Reynolds numbers). Another variation it to impose periodic conditions in the y-direction - which gives us an array of cylinders rather than just one cylinder. There has also been work done simulating the response of spinning cylinders both in a free stream and near walls.
Literature
There are a tremendous number of references for that problem. Here is a selection of some:
[1] Ahmad, R.A., 1996, Steady-state numerical solution of the Navier-Stokes and energy equations around a horizontal cylinder at moderate Reynolds numbers from 100 to 500, Heat Transfer Engg., 17: 31-81.
[2] Chakraborty, J., Verma, N. and Chhabra, R. P., 2004, Wall effects in the flow past a circular cylinder in a plane channel: a numerical study, Chem. Engng. Processing, 43: 1529-1537.
[3] Coutanceau, M. and Bouard, R., 1977, Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1: Steady flow, J. Fluid Mech., 79: 231-256.
[4] Coutanceau, M. and Defaye, J.-R., 1991 Circular cylinder wake configurations: a flow visualization survey, Appl. Mech. Rev., 44: 255-305.
[5] D'Alessio, S. J. D. and Dennis, S. C. R., 1994, A vorticity model for viscous flow past a cylinder, Comp. Fluids, 23: 279-293.
[6] Dennis, S. C. R. and Chang, G.-Z., 1970, Numerical solutions for steady flow past a circular cylinder at Reynolds number up to 100, J. Fluid Mech., 42: 471-489.
[7] Dennis, S. C. R. and Hudson, J. D., 1995, An $h^4$ accurate vorticity-velocity formulation for calculating flow past circular cylinder, Int. J. Numer. Meth. Fluids, 21: 489-497.
[8]Dennis, S. C. R., Hudson, J. D. and Smith, N., 1968, Steady laminar forced convection from a circular cylinder at low Reynolds numbers, Phys. Fluids, 11: 933-940.
[9]Fornberg, B., 1980, A numerical study of steady viscous flow past a circular cylinder, J. Fluid Mech., 98: 819-855.
[10] Fornberg, B., 1985, Steady viscous flow past a circular cylinder up to Reynolds number 600, J. Comp. Phys., 61: 297-320.
[11] Ding, H., Shu, C., Yeo, K. S. and Xu, D., 2004, Simulations of incompressible viscous flows past a circular cylinder by hybrid FD scheme and meshless least square-based finite difference scheme, Comput. Methods Appl. Mech. Engng., 193: 727-744.
[12] Hamielec, A. E. and Raal, J. D., 1969, Numerical studies of viscous flow around circular cylinders, Phys. Fluids, 12: 11-17.
[13] Kawaguti, M. and Jain, P., 1966, Numerical study of a viscous flow past a circular cylinder, J. Phys. Soc. Jpn., 21: 2055-2062.
[14] Sucker, D. and Brauer, H., 1975, Fluiddynamik bei quer angeströmten Zylindern, Wärme- and Stoffübertragung, 8: 149-158.
[15] Takami, H. and Keller, H. B., 1969, Steady two-dimensional viscous flow of an incompressible fluid past a circular cylinder, High-Speed Computing in Fluid Dynamics The Phys. Fluids Supplement II, 12: 51-56.
[16] Isaev S. A., Leontiev A. I., Kudryavtsev N. A., Baranova T. A., Lysenko D. A. (2005). Numerical Simulation of Unsteady-State Heat Transfer under Conditions of Laminar Transverse Flow past a Circular Cylinder, High Temperature. Vol. 43, No. 5, pp. 746–759
[17] Isaev S.A., Baranov P.A., Kudryavtsev N.A., Lysenko D.A., Usachov A.E. (2005). Comparative analysis of the calculation data on an unsteady flow around a circular cylinder obtained using the VP2/3 and Fluent packages and the Spalart-Allmaras and Menter turbulence models // J. Engineering Physics and Thermophysics. Vol.78. No.6. pp. 1199-2013.
[18] M.M. Zdravkovich, Flow Around Circular Cylinders, Vol. 1 Fundamentals, Oxford University Press, 1997
[19] M.M. Zdravkovich, Flow Around Circular Cylinders, Vol. 2 Applications, Oxford University Press, 2003
[20] Norberg, C. (2003). Fluctuating lift on a circular cylinder: Review and new measurements, Journal of Fluids and Structures 17 (1), pp. 57-96 29
[21] Norberg, C. (2001). Flow around a circular cylinder: Aspects of fluctuating lift, Journal of Fluids and Structures 15 (3-4), pp. 459-469
[22] Norberg, C. (1994). Experimental investigation of the flow around a circular cylinder: influence of aspect ratio, Journal of Fluid Mechanics 258, pp. 287-316 96
[23] Norberg, C., Sunden, B. J. (1987). Turbulence and Reynolds number effects on the flow and fluid forces on a single cylinder in cross flow, FLUIDS & STRUCT. 1 (3 , Jul. 1987), pp. 337-357 9
[24] Norberg, C. (1985). INTERACTION BETWEEN FREESTREAM TURBULENCE AND VORTEX SHEDDING FOR A SINGLE TUBE IN CROSS-FLOW, Journal of Wind Engineering and Industrial Aerodynamics 23 (1-3), pp. 501-514