Free-Surface Piercing NACA 0024 Hydrofoil
From CFD-Wiki
(→Mesh) |
m (→Mesh) |
||
| Line 7: | Line 7: | ||
==Mesh== | ==Mesh== | ||
| - | + | <br> | |
[[Image:vofnaca0024meshdetails.jpg]]<br><br> | [[Image:vofnaca0024meshdetails.jpg]]<br><br> | ||
The mesh for this problem contains 118,800 cells. The solution is time dependent. I monitor the drag coefficient on the profile to see when the problem has reached a stationary solution. I start with a flat free-surface and run the calculations on a coarse mesh. Then I use the solution of the coarse mesh as an initial solution for the fine mesh. | The mesh for this problem contains 118,800 cells. The solution is time dependent. I monitor the drag coefficient on the profile to see when the problem has reached a stationary solution. I start with a flat free-surface and run the calculations on a coarse mesh. Then I use the solution of the coarse mesh as an initial solution for the fine mesh. | ||
Revision as of 12:47, 16 October 2009
Contents |
Introduction
This is a validation case for a 3-dimensional Volume of Fluid [Ref. 1] method.
The above picture was taken from Ref. 2. It is a photograph of the experimental setup of the surface piercing foil. It shows a NACA 0024 profile with a chord of 1.2 m, which moves horizontally through the water at a velocity of 1.27 m s-1. This situation corresponds to a Froude number of 0.37 and a Reynold’s number of 1.52E6. When the flow has evolved to a steady situation, the height of the free-surface is measured at a number of positions along the profile.
Mesh
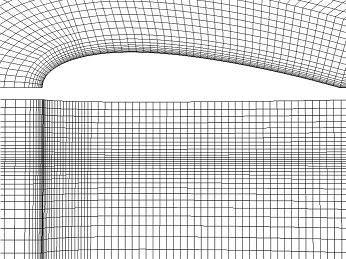
The mesh for this problem contains 118,800 cells. The solution is time dependent. I monitor the drag coefficient on the profile to see when the problem has reached a stationary solution. I start with a flat free-surface and run the calculations on a coarse mesh. Then I use the solution of the coarse mesh as an initial solution for the fine mesh.
Results
References
1. C.W. Hirt, B.D. Nichols, Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries, J. Comp. Phys. 39, pp. 201-225 (1981)
2. Shin Hyung Rhee, Boris P. Makarov, H. Krishinan, Vladimir Ivanov, Assessment of the volume of fluid method for free-surface wave flow, J. Mar. Sci. Technol. 10, pp. 173-180 (2005)

