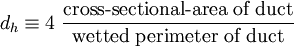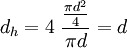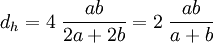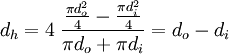Hydraulic diameter
From CFD-Wiki
(Difference between revisions)
m |
|||
| Line 5: | Line 5: | ||
:<math>d_h \equiv 4 \; \frac{\mbox{cross-sectional-area of duct}}{\mbox{wetted perimeter of duct}}</math> | :<math>d_h \equiv 4 \; \frac{\mbox{cross-sectional-area of duct}}{\mbox{wetted perimeter of duct}}</math> | ||
| - | ==Circular pipe== | + | ==Use of hydraulic diameter== |
| + | |||
| + | ==Hydraulic diameters for different duct-geometries== | ||
| + | |||
| + | Using the definition above the hydraulic diamater can easily be computed for any type of duct-geometry. Below follows a few examples. | ||
| + | |||
| + | ===Circular pipe=== | ||
For a circular pipe or hole the hydraulic diamater is: | For a circular pipe or hole the hydraulic diamater is: | ||
| Line 13: | Line 19: | ||
Where d is the real diameter of the pipe. Hence, for circular pipes the hydraulic diameter is the same as the real diameter of the pipe. | Where d is the real diameter of the pipe. Hence, for circular pipes the hydraulic diameter is the same as the real diameter of the pipe. | ||
| - | ==Rectangular tube== | + | ===Rectangular tube=== |
For a rectangular tube or hole with the width <math>a</math> and the height <math>b</math> the hydraulic diamter is: | For a rectangular tube or hole with the width <math>a</math> and the height <math>b</math> the hydraulic diamter is: | ||
| Line 19: | Line 25: | ||
:<math>d_h = 4 \; \frac{a b}{2 a + 2 b} = 2 \; \frac{a b}{a + b}</math> | :<math>d_h = 4 \; \frac{a b}{2 a + 2 b} = 2 \; \frac{a b}{a + b}</math> | ||
| - | ==Coaxial circular tube== | + | ===Coaxial circular tube=== |
For a coaxial circular tube with an inner diameter <math>d_i</math> and an outer diameter <math>d_o</math> the hydraulic diameter is: | For a coaxial circular tube with an inner diameter <math>d_i</math> and an outer diameter <math>d_o</math> the hydraulic diameter is: | ||
:<math>d_h = 4 \; \frac{\frac{\pi d_o^2}{4} - \frac{\pi d_i^2}{4}}{\pi d_o + \pi d_i} = d_o - d_i</math> | :<math>d_h = 4 \; \frac{\frac{\pi d_o^2}{4} - \frac{\pi d_i^2}{4}}{\pi d_o + \pi d_i} = d_o - d_i</math> | ||
Revision as of 13:56, 24 March 2006
The hydraulic diameter, 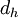 , is commonly used when dealing with non-circular pipes, holes or ducts.
, is commonly used when dealing with non-circular pipes, holes or ducts.
The definition of the hydraulic diamater is:
Contents |
Use of hydraulic diameter
Hydraulic diameters for different duct-geometries
Using the definition above the hydraulic diamater can easily be computed for any type of duct-geometry. Below follows a few examples.
Circular pipe
For a circular pipe or hole the hydraulic diamater is:
Where d is the real diameter of the pipe. Hence, for circular pipes the hydraulic diameter is the same as the real diameter of the pipe.
Rectangular tube
For a rectangular tube or hole with the width 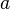 and the height
and the height 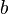 the hydraulic diamter is:
the hydraulic diamter is:
Coaxial circular tube
For a coaxial circular tube with an inner diameter 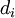 and an outer diameter
and an outer diameter 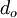 the hydraulic diameter is:
the hydraulic diameter is: