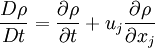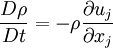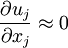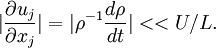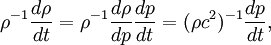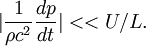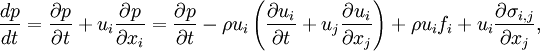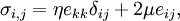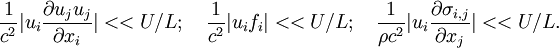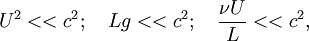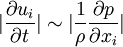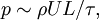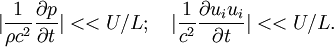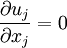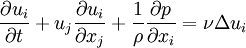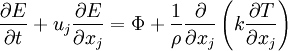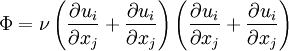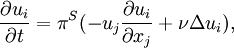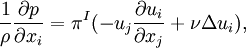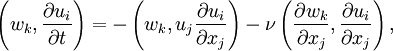Incompressible flow
From CFD-Wiki
Pete Bachant (Talk | contribs) (→Dimensional analysis) |
|||
| (21 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
A flow is said to be incompressible if the density of a fluid element does not change during its motion. It is a property of the flow and not of the fluid. The rate of change of density of a material fluid element is given by the material derivative | A flow is said to be incompressible if the density of a fluid element does not change during its motion. It is a property of the flow and not of the fluid. The rate of change of density of a material fluid element is given by the material derivative | ||
| - | <math> | + | :<math> |
\frac{D \rho}{D t} = \frac{\partial \rho}{\partial t} + u_j \frac{\partial \rho}{\partial x_j} | \frac{D \rho}{D t} = \frac{\partial \rho}{\partial t} + u_j \frac{\partial \rho}{\partial x_j} | ||
</math> | </math> | ||
| Line 7: | Line 7: | ||
From the continuity equation we have | From the continuity equation we have | ||
| - | <math> | + | :<math> |
\frac{D \rho}{D t} = - \rho \frac{\partial u_j}{\partial x_j} | \frac{D \rho}{D t} = - \rho \frac{\partial u_j}{\partial x_j} | ||
</math> | </math> | ||
Hence the flow is incompressible if the divergence of the velocity field is identically zero. Note that the density field need not be uniform in an incompressible flow. All that is required is that the density of a fluid element should not change in time as it moves through space. For example, flow in the ocean can be considered to be incompressible even though the density of water is not uniform due to stratification. | Hence the flow is incompressible if the divergence of the velocity field is identically zero. Note that the density field need not be uniform in an incompressible flow. All that is required is that the density of a fluid element should not change in time as it moves through space. For example, flow in the ocean can be considered to be incompressible even though the density of water is not uniform due to stratification. | ||
| + | |||
| + | [[Compressible flow]] can with good accuracy be approximated as incompressible for steady flow if the [[Mach number]] is below 0.3. | ||
| + | |||
| + | == Dimensional analysis == | ||
| + | |||
| + | Assume <math>L</math> is the characteristic length, <math>U</math> is the characteristic velocity, the magnitude of velocity gradient is <math>U/L</math>. The physical meaning of the incompressible flow is | ||
| + | :<math> | ||
| + | \frac{\partial u_j}{\partial x_j} \approx 0 | ||
| + | </math> | ||
| + | |||
| + | or | ||
| + | |||
| + | :<math> | ||
| + | |\frac{\partial u_j}{\partial x_j}|=|\rho^{-1}\frac{d\rho}{dt}| << U/L. | ||
| + | </math> | ||
| + | |||
| + | It is know that | ||
| + | :<math> | ||
| + | \rho^{-1}\frac{d\rho}{dt}=\rho^{-1}\frac{d\rho}{dp}\frac{dp}{dt}=(\rho c^2)^{-1}\frac{dp}{dt}, | ||
| + | </math> | ||
| + | where <math>c</math> is the sound speed. Hence, the incompressible condition is, | ||
| + | |||
| + | :<math> | ||
| + | |\frac{1}{\rho c^2}\frac{dp}{dt}|<<U/L. | ||
| + | </math> | ||
| + | |||
| + | In general, for the liquid, <math>\rho=const</math> and <math>\frac{\rho}{dt}=0</math>. So the question is that under what contion, the gas flow can be taken as incompressible flow? | ||
| + | |||
| + | We have | ||
| + | :<math> | ||
| + | \frac{dp}{dt}=\frac{\partial p}{\partial t}+u_i\frac{\partial p}{\partial x_i}=\frac{\partial p}{\partial t}-\rho u_i\left(\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}\right)+\rho u_i f_i+u_i \frac{\partial \sigma_{i,j}}{\partial x_j}, | ||
| + | </math> | ||
| + | where <math>f_i</math> is the body force (taken as gravitational force in the present document), <math>\sigma_{i,j}</math> is the stress tensor defined as, | ||
| + | :<math> | ||
| + | \sigma_{i,j}=\eta e_{kk}\delta_{ij}+2\mu e_{ij}, | ||
| + | </math> | ||
| + | where <math>e_{ij}=\frac{1}{2}(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i})</math>. | ||
| + | |||
| + | Then we can summarize as following, | ||
| + | * Steady incompressible flow | ||
| + | The steady flow can be taken as incompressible flow under the following conditions, | ||
| + | :<math> | ||
| + | \frac{1}{c^2}|u_i\frac{\partial u_ju_j}{\partial x_i}|<<U/L;\quad \frac{1}{c^2}|u_if_i|<<U/L;\quad \frac{1}{\rho c^2}|u_i \frac{\partial \sigma_{i,j}}{\partial x_j}|<<U/L. | ||
| + | </math> | ||
| + | Then it arrives, | ||
| + | :<math> | ||
| + | U^2<<c^2;\quad Lg<<c^2;\quad \frac{\nu U}{L}<<c^2, | ||
| + | </math> | ||
| + | where <math>\nu=\frac{\mu,\eta}{\rho}</math>. | ||
| + | |||
| + | If <math>L<10m</math>, <math>Lg<<c^2</math> holds; <math>\nu=c\lambda</math>, so <math>U<<\frac{Lc}{\lambda}</math> (<math>\lambda</math> is the molecular free path) holds naturally for the continuous medium. | ||
| + | |||
| + | So for the steady flow, it can be taken as incompressible flow when <math>U<<c</math>, i.e. <math>Ma<<1</math>. In general, the flow will be taken as incompressible flow when <math>Ma\le 0.3</math>. | ||
| + | |||
| + | * Unsteady incompressible flow | ||
| + | For unsteady flow, if <math>|\frac{\partial }{\partial t}|\sim|u_i\frac{\partial }{\partial x_i}|</math>, the flow is incompressible when <math>Ma<<1</math>. But if <math>|\frac{\partial }{\partial t}|>>|u_i\frac{\partial }{\partial x_i}|</math>, it needs to figure out the condition. It is known that | ||
| + | :<math> | ||
| + | |\frac{\partial u_i}{\partial t}|\sim|\frac{1}{\rho}\frac{\partial p}{\partial x_i}| | ||
| + | </math> | ||
| + | Hence, | ||
| + | :<math> | ||
| + | p\sim \rho U L/\tau, | ||
| + | </math> | ||
| + | where <math>\tau</math> is the characteristic time. | ||
| + | |||
| + | If <math>\tau>> L/c</math>, then <math>\tau>> LU/c^2</math>, and we get | ||
| + | :<math> | ||
| + | |\frac{1}{\rho c^2}\frac{\partial p}{\partial t}|<<U/L; \quad |\frac{1}{c^2}\frac{\partial u_i u_i}{\partial t}|<<U/L. | ||
| + | </math> | ||
| + | |||
| + | So for this case, the flow can be taken as incompressible flow when <math>\tau>>L/c</math>. | ||
| + | |||
| + | * Low speed atmospheric motion | ||
| + | For the atmospheric motion, one more condition is needed, <math>|\frac{u_i f_i}{c^2}|<<U/L</math>, i.e. <math>L<<c^2/g\sim 10^4</math>. But the characteristic length for the atmospheric motion is more than 10 km, the low speed atmospheric motion is not incompressible flow. | ||
| + | |||
| + | * Question for thinking: is the sound wave compresible or incompressible wave? Why? | ||
== Governing Equations == | == Governing Equations == | ||
| - | The [[Navier | + | |
| + | The [[Navier-Stokes equations]] for incompressible flow are | ||
* Continuity equation | * Continuity equation | ||
| - | <math> | + | :<math> |
\frac{\partial u_j}{\partial x_j} = 0 | \frac{\partial u_j}{\partial x_j} = 0 | ||
</math> | </math> | ||
| Line 24: | Line 101: | ||
* Momentum equation | * Momentum equation | ||
| - | <math> | + | :<math> |
\frac{\partial u_i}{\partial t} + u_j \frac{\partial u_i}{\partial x_j} + \frac{1}{\rho} \frac{\partial p}{\partial x_i} = \nu \Delta u_i | \frac{\partial u_i}{\partial t} + u_j \frac{\partial u_i}{\partial x_j} + \frac{1}{\rho} \frac{\partial p}{\partial x_i} = \nu \Delta u_i | ||
</math> | </math> | ||
| Line 30: | Line 107: | ||
* Energy equation | * Energy equation | ||
| - | <math> | + | :<math> |
\frac{\partial E}{\partial t} + u_j \frac{\partial E}{\partial x_j} = \Phi + \frac{1}{\rho} \frac{\partial}{\partial x_j} \left( k \frac{\partial T}{\partial x_j} \right) | \frac{\partial E}{\partial t} + u_j \frac{\partial E}{\partial x_j} = \Phi + \frac{1}{\rho} \frac{\partial}{\partial x_j} \left( k \frac{\partial T}{\partial x_j} \right) | ||
</math> | </math> | ||
| Line 41: | Line 118: | ||
* <math>\Phi</math> is the rate of dissipation of mechanical energy per unit mass | * <math>\Phi</math> is the rate of dissipation of mechanical energy per unit mass | ||
| - | <math> | + | :<math> |
\Phi = \nu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_i}{\partial x_j} \right) | \Phi = \nu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_i}{\partial x_j} \right) | ||
\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_i}{\partial x_j} \right) | \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_i}{\partial x_j} \right) | ||
| Line 49: | Line 126: | ||
* k is the coefficient of thermal conductivity | * k is the coefficient of thermal conductivity | ||
* T is the temperature | * T is the temperature | ||
| + | |||
| + | However, the momentum equation is a composite equation, being the sum of the two equations, | ||
| + | :<math> | ||
| + | \frac{\partial u_i}{\partial t} = \pi^S (-u_j \frac{\partial u_i}{\partial x_j} + \nu \Delta u_i) , | ||
| + | </math> | ||
| + | :<math> | ||
| + | \frac{1}{\rho} \frac{\partial p}{\partial x_i} = \pi^I (-u_j \frac{\partial u_i}{\partial x_j} + \nu \Delta u_i), | ||
| + | </math> | ||
| + | which result from the Helmholtz decomposition. <math>\pi^S</math> and <math>\pi^I</math> are the solenoidal (divergence-free) and irrotational projection operators. | ||
| + | |||
| + | The divergence-free governing equation for the velocity is pressure-free, calling into question the interpretation of the pressure as the enforcer of continuity. Rather, this equation should be considered a kinematic equation with continuity as a conservation law. The equation for the pressure as a functional of the velocity can be recognized as a form of the pressure poisson equation. | ||
| + | |||
| + | If expressions for the projection operators are inserted, it is clear that these are integro-differential equations, rather than the differential-algebraic form of the composite equation. This inconvenience can be eliminated by use of the equivalent weak form, | ||
| + | :<math> | ||
| + | \left(w_k,\frac{\partial u_i}{\partial t}\right) = -\left(w_k,u_j \frac{\partial u_i}{\partial x_j}\right)-\nu \left(\frac{\partial w_k}{\partial x_j},\frac{\partial u_i}{\partial x_j}\right) , | ||
| + | </math> | ||
| + | where the weight functions <math>w</math> are divergence-free. The function of the projection operator has been replaced by the orthogonality of solenoidal and irrotational function spaces. Cast in discrete form, this forms the basis for finite element computations. | ||
| + | |||
| + | A question immediately comes to mind: If the governing equation does not involve the pressure, how does one specify boundary conditions for pressure-driven (Poiseuille) flow? A divergence-free field implies the existence of a stream function (or vector potential in 3D) <math>\Psi</math> such that the velocity field is the curl of <math>\Psi</math>. Then specifying <math>\Psi</math> on a part of the boundary determines the flow from the Stokes theorem. | ||
| + | |||
| + | |||
== Physical characteristics == | == Physical characteristics == | ||
| - | |||
| - | If the viscosity is assumed to be constant then the energy equation is decoupled from the continuity and momentum equations. | + | A consequence of incompressible flow is that there is no equation of state for pressure, unlike in [[compressible flow]]. Since there is no separate equation for pressure, it must be obtained from the continuity and momentum equations. The main role of pressure is to satisfy the zero divergence condition of the velocity field. Note that pressure is only determined up to a constant. |
| + | |||
| + | If the viscosity is assumed to be constant, then the energy equation is decoupled from the continuity and momentum equations. | ||
Revision as of 16:21, 20 July 2013
A flow is said to be incompressible if the density of a fluid element does not change during its motion. It is a property of the flow and not of the fluid. The rate of change of density of a material fluid element is given by the material derivative
From the continuity equation we have
Hence the flow is incompressible if the divergence of the velocity field is identically zero. Note that the density field need not be uniform in an incompressible flow. All that is required is that the density of a fluid element should not change in time as it moves through space. For example, flow in the ocean can be considered to be incompressible even though the density of water is not uniform due to stratification.
Compressible flow can with good accuracy be approximated as incompressible for steady flow if the Mach number is below 0.3.
Dimensional analysis
Assume 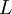 is the characteristic length,
is the characteristic length, 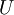 is the characteristic velocity, the magnitude of velocity gradient is
is the characteristic velocity, the magnitude of velocity gradient is 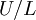 . The physical meaning of the incompressible flow is
. The physical meaning of the incompressible flow is
or
It is know that
where 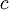 is the sound speed. Hence, the incompressible condition is,
is the sound speed. Hence, the incompressible condition is,
In general, for the liquid, 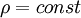 and
and 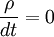 . So the question is that under what contion, the gas flow can be taken as incompressible flow?
. So the question is that under what contion, the gas flow can be taken as incompressible flow?
We have
where 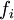 is the body force (taken as gravitational force in the present document),
is the body force (taken as gravitational force in the present document), 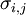 is the stress tensor defined as,
is the stress tensor defined as,
where 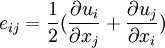 .
.
Then we can summarize as following,
- Steady incompressible flow
The steady flow can be taken as incompressible flow under the following conditions,
Then it arrives,
where 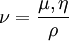 .
.
If 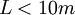 ,
, 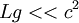 holds;
holds; 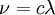 , so
, so 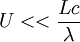 (
(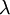 is the molecular free path) holds naturally for the continuous medium.
is the molecular free path) holds naturally for the continuous medium.
So for the steady flow, it can be taken as incompressible flow when 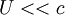 , i.e.
, i.e. 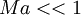 . In general, the flow will be taken as incompressible flow when
. In general, the flow will be taken as incompressible flow when 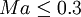 .
.
- Unsteady incompressible flow
For unsteady flow, if 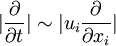 , the flow is incompressible when
, the flow is incompressible when 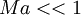 . But if
. But if 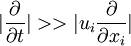 , it needs to figure out the condition. It is known that
, it needs to figure out the condition. It is known that
Hence,
where 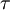 is the characteristic time.
is the characteristic time.
If 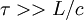 , then
, then 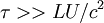 , and we get
, and we get
So for this case, the flow can be taken as incompressible flow when 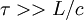 .
.
- Low speed atmospheric motion
For the atmospheric motion, one more condition is needed, 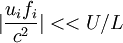 , i.e.
, i.e. 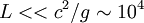 . But the characteristic length for the atmospheric motion is more than 10 km, the low speed atmospheric motion is not incompressible flow.
. But the characteristic length for the atmospheric motion is more than 10 km, the low speed atmospheric motion is not incompressible flow.
- Question for thinking: is the sound wave compresible or incompressible wave? Why?
Governing Equations
The Navier-Stokes equations for incompressible flow are
- Continuity equation
- Momentum equation
- Energy equation
where
-
 is the Laplacian operator
is the Laplacian operator
- E is the internal energy per unit mass
-
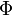 is the rate of dissipation of mechanical energy per unit mass
is the rate of dissipation of mechanical energy per unit mass
-
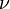 is the kinematic viscosity
is the kinematic viscosity
- k is the coefficient of thermal conductivity
- T is the temperature
However, the momentum equation is a composite equation, being the sum of the two equations,
which result from the Helmholtz decomposition. 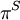 and
and 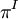 are the solenoidal (divergence-free) and irrotational projection operators.
are the solenoidal (divergence-free) and irrotational projection operators.
The divergence-free governing equation for the velocity is pressure-free, calling into question the interpretation of the pressure as the enforcer of continuity. Rather, this equation should be considered a kinematic equation with continuity as a conservation law. The equation for the pressure as a functional of the velocity can be recognized as a form of the pressure poisson equation.
If expressions for the projection operators are inserted, it is clear that these are integro-differential equations, rather than the differential-algebraic form of the composite equation. This inconvenience can be eliminated by use of the equivalent weak form,
where the weight functions 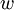 are divergence-free. The function of the projection operator has been replaced by the orthogonality of solenoidal and irrotational function spaces. Cast in discrete form, this forms the basis for finite element computations.
are divergence-free. The function of the projection operator has been replaced by the orthogonality of solenoidal and irrotational function spaces. Cast in discrete form, this forms the basis for finite element computations.
A question immediately comes to mind: If the governing equation does not involve the pressure, how does one specify boundary conditions for pressure-driven (Poiseuille) flow? A divergence-free field implies the existence of a stream function (or vector potential in 3D) 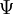 such that the velocity field is the curl of
such that the velocity field is the curl of 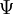 . Then specifying
. Then specifying 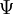 on a part of the boundary determines the flow from the Stokes theorem.
on a part of the boundary determines the flow from the Stokes theorem.
Physical characteristics
A consequence of incompressible flow is that there is no equation of state for pressure, unlike in compressible flow. Since there is no separate equation for pressure, it must be obtained from the continuity and momentum equations. The main role of pressure is to satisfy the zero divergence condition of the velocity field. Note that pressure is only determined up to a constant.
If the viscosity is assumed to be constant, then the energy equation is decoupled from the continuity and momentum equations.