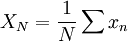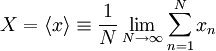Introduction to turbulence/Statistical analysis
From CFD-Wiki
(→The mean or ensemble average) |
(→The mean or ensemble average) |
||
| Line 47: | Line 47: | ||
In general, the <math> x_{n}</math> couldbe realizations of any random variable. The <math> X </math> defined by equation 2.2 representsthe ensemble average of it. The quantity <math> X </math> is sometimes referred to as the ''expacted value '' of the random variables <math> x </math> , or even simple its ''mean''. | In general, the <math> x_{n}</math> couldbe realizations of any random variable. The <math> X </math> defined by equation 2.2 representsthe ensemble average of it. The quantity <math> X </math> is sometimes referred to as the ''expacted value '' of the random variables <math> x </math> , or even simple its ''mean''. | ||
| - | For example, the velocity vector at a given point in space and time <math> x^{\rightarrow},t </math> , in a given turbulent flow can be considered to be a random variable, say <math> u_{i} \left( x^{\rightarrow},t \right) </math> | + | For example, the velocity vector at a given point in space and time <math> x^{\rightarrow},t </math> , in a given turbulent flow can be considered to be a random variable, say <math> u_{i} \left( x^{\rightarrow},t \right) </math>. If there were a large number of identical experiments so that the <math> u^{n}_{i} \left( x^{\rightarrow},t \right) </math> in each of them were identically distributed, then the ensemble average |
Revision as of 01:25, 17 May 2006
1 Foreword
Much of the study of turbulence requires statistics and stochastic processes, simply because the instanteous motions are too complicated to understand. This should not be taken to mean that the govering equations (usually the Navier-Stokes equations) are stochastic. Even simple non-linear equations can have deterministic solutions that look random. In other words, even though the solutions for a given set of initial and boundary conditions can be perfectly repeatable and predictable at a given time and point in space, it may be impossible to guess from the information at one point or time how it will behave at another (at least without solving the equations). Moreover, a slight change in the intial or boundary conditions may cause large changes in the solution at a given time and location; in particular, changes that we could not have anticipated.
Here will be introduced the simple idea of the ensemble average
Most of the statistical analyses of turbulent flows are based on the idea of an ensemble average in one form or another. In some ways this is rather inconvenient, since it will be obvious from the definitions that it is impossible to ever really measure such a quantity. Therefore we will spendlast part of this chapter talking about how the kind of averages we can compute from data correspond to the hypotetical ensemble average we wish we could have measured. In later chapters we shall introduce more statistical concepts as we require them. But the concepts of this chapter will be all we need to begin a discussion of the averaged equations of motion in Chapter 3
The ensemble and Ensemble Average
The mean or ensemble average
The concept of an ensebmble average is based upon the existence of independent statistical event. For example, consider a number of inviduals who are simultaneously flipping unbiased coins. If a value of one is assigned to a head and the value of zero to a tail, then the average of the numbers generated is defined as
|
| (2) |
where our 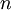 th flip is denoted as
th flip is denoted as 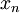 and
and 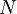 is the total number of flips.
is the total number of flips.
Now if all the coins are the same, it doesn't really matter whether we flip one coin 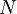 times, or
times, or 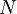 coins a single time. The key is that they must all be independent events - meaning the probability of achieving a head or tail in a given flip must be completely independent of what happens in all the other flips. Obviously we can't just flip one coin and count it
coins a single time. The key is that they must all be independent events - meaning the probability of achieving a head or tail in a given flip must be completely independent of what happens in all the other flips. Obviously we can't just flip one coin and count it 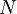 times; these cleary would not be independent events
times; these cleary would not be independent events
Unless you had a very unusual experimental result, you probably noticed that the value of the 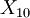 's was also a random variable and differed from ensemble to ensemble. Also the greater the number of flips in the ensemle, thecloser you got to
's was also a random variable and differed from ensemble to ensemble. Also the greater the number of flips in the ensemle, thecloser you got to 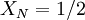 . Obviously the bigger
. Obviously the bigger 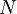 , the less fluctuation there is in
, the less fluctuation there is in 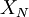
Now imagine that we are trying to establish the nature of a random variable 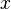 . The
. The 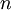 th realization of
th realization of 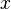 is denoted as
is denoted as 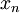 . The ensemble average of
. The ensemble average of 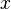 is denoted as
is denoted as 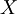 (or
(or 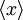 ), and is defined as
), and is defined as
|
| (2) |
Obviously it is impossible to obtain the ensemble average experimentally, since we can never an infinite number of independent realizations. The most we can ever obtain is the ariphmetic mean for the number of realizations we have. For this reason the arithmetic mean can also referred to as the estimator for the true mean ensemble average.
Even though the true mean (or ensemble average) is unobtainable, nonetheless, the idea is still very useful. Most importantly,we can almost always be sure the ensemble average exists, even if we can only estimate what it really is. The fact of its existence, however, does not always mean that it is easy to obtain in practice. All the theoretical deductions in this course will use this ensemble average. Obviously this will mean we have to account for these "statistical differenced" between true means and estimates when comparing our theoretical results to actual measurements or computations.
In general, the 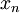 couldbe realizations of any random variable. The
couldbe realizations of any random variable. The 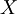 defined by equation 2.2 representsthe ensemble average of it. The quantity
defined by equation 2.2 representsthe ensemble average of it. The quantity 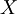 is sometimes referred to as the expacted value of the random variables
is sometimes referred to as the expacted value of the random variables 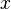 , or even simple its mean.
, or even simple its mean.
For example, the velocity vector at a given point in space and time 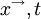 , in a given turbulent flow can be considered to be a random variable, say
, in a given turbulent flow can be considered to be a random variable, say 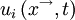 . If there were a large number of identical experiments so that the
. If there were a large number of identical experiments so that the 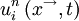 in each of them were identically distributed, then the ensemble average
in each of them were identically distributed, then the ensemble average