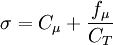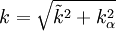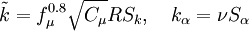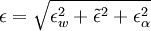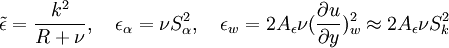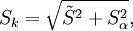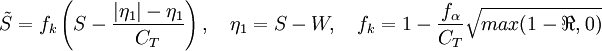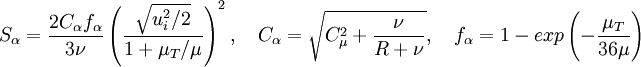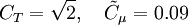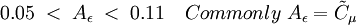Rahman-Siikonen-Agarwal Model
From CFD-Wiki
(Difference between revisions)
(→Introduction) |
(→Introduction) |
||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
| - | The Rahman | + | The Rahman-Agarwal-Siikonen (RAS) Turbulence model is a one-equation eddy viscosity model based on <math>k-\epsilon</math> closure. The R-transport equation along with the Bradshaw and other empirical relations are used to solve for the turbulent viscosity. A damping function, <math>f_\mu</math>, is used to represent the kinematic blocking by the wall. To avoid defining a wall distance, a Helmholtz-type elliptic relaxation equation is used for <math>f_\mu</math>. The model has been validated against a few well-documented flow cases, yielding predictions in good agreement with DNS and experimental data. |
== RAS Model == | == RAS Model == | ||
Latest revision as of 19:47, 8 July 2013
Introduction
The Rahman-Agarwal-Siikonen (RAS) Turbulence model is a one-equation eddy viscosity model based on 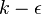 closure. The R-transport equation along with the Bradshaw and other empirical relations are used to solve for the turbulent viscosity. A damping function,
closure. The R-transport equation along with the Bradshaw and other empirical relations are used to solve for the turbulent viscosity. A damping function, 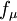 , is used to represent the kinematic blocking by the wall. To avoid defining a wall distance, a Helmholtz-type elliptic relaxation equation is used for
, is used to represent the kinematic blocking by the wall. To avoid defining a wall distance, a Helmholtz-type elliptic relaxation equation is used for 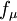 . The model has been validated against a few well-documented flow cases, yielding predictions in good agreement with DNS and experimental data.
. The model has been validated against a few well-documented flow cases, yielding predictions in good agreement with DNS and experimental data.
RAS Model
The turbulent eddy viscosity is given by
The R-transport Equation:
Realizable Time Scale:
Coefficient 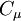 :
:
Damping Function:
Other Model Coefficients:
 and
and  :
:
Constants:
References
- Rahman, M. M., Siikonen, T., and Agarwal, R. K. (2011), "Improved Low Re-Number One-Equation Turbulence Model", AIAA Vol. 49, No.4, April 2011.

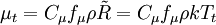
![\begin{matrix}
\frac{\partial \rho R}{\partial t} + \frac{\partial \rho u_j R}{\partial x_j} = \frac{\partial}{\partial x_j} \biggl[ \left(\mu +\frac{\mu_t}{\sigma}\right)\frac{\partial R}{\partial x_j} \biggr] +C_1 \rho \sqrt{P \tilde{R}} - C_2 \rho \left(\frac{\partial \tilde{R}}{\partial x_k}\right)^2
\end{matrix}](/W/images/math/d/3/2/d3291f6d4f59689da557c0eef4170cd4.png)
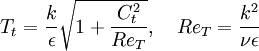
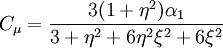

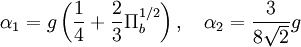
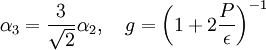
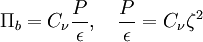
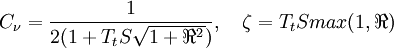
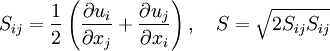
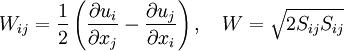
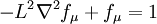
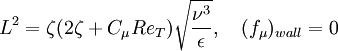
![C_1 = 2C_\mu \zeta (1-C_\mu \zeta), \quad C_2 = min \Biggl[ 2C_\mu,\; \tilde{C}_\mu \sqrt{1+\left( \frac{C_1}{6 \tilde{C}_\mu}\right)^2}\;\Biggr]](/W/images/math/4/a/7/4a7662c3bf356b3a87d6eb5a62cd91a7.png)