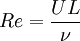Reynolds number
From CFD-Wiki
The Reynolds number is probably the single most important parameter in fluid dynamics. It characterises the relative importance of inertial and viscous forces in a flow. It is important in determining the state of the flow, whether it is laminar or turbulent. At high Reynolds numbers flows generally tend to be turbulent, which was first recognized by Osborne Reynolds in his famous pipe flow experiments. Consider the momentum equation which is given below
![\frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_i u_j + p \delta_{ij} \right] = \frac{\partial}{\partial x_j} \tau_{ij}](/W/images/math/2/9/2/292803eddd8e701579bdb8e0f9307a89.png)
The terms on the right are the inertial forces and those on the left correspond to viscous forces. If 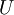 ,
, 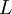 ,
, 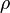 and
and 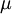 are the reference values for velocity, length, density and dynamic viscosity, then
are the reference values for velocity, length, density and dynamic viscosity, then
inertial force ~ 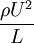
viscous force ~ 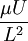
Their ratio is the Reynolds number, usually denoted as 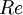
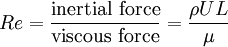
In terms of the kinematic viscosity
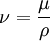
the Reynolds number is given by