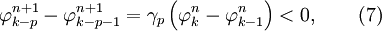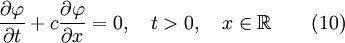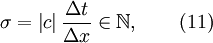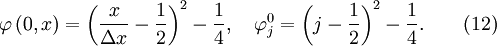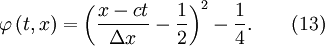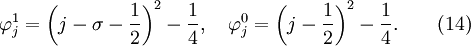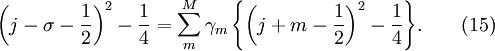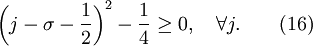Sand box Approximation Schemes
From CFD-Wiki
In numerical analysis and computational fluid dynamics, Godunov's theorem — also known as Godunov's order barrier theorem — is a mathematical theorem important in the development of the theory of high resolution schemes for the numerical solution of partial differential equations.
The theorem states that:
- Linear numerical schemes for solving partial differential equations (PDE's), having the property of not generating new extrema (monotone scheme), can be at most first-order accurate.
Professor Sergei K. Godunov originally proved the theorem as a Ph.D. student at Moscow State University. It is his most influential work in the area of applied and numerical mathematics and has had a major impact on science and engineering, particularly in the development of methodologies used in computational fluid dynamics (CFD) and other computational fields. One of his major contributions was to prove the theorem (Godunov, 1954; Godunov, 1959), that bears his name.
Contents |
The theorem
We generally follow Wesseling (2001).
Aside
Assume a continuum problem described by a PDE is to be computed using a numerical scheme based upon a uniform computational grid and a one-step, constant step-size, M grid point, integration algorithm, either implicit or explicit. Then if 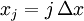 and
and 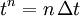 , such a scheme can be described by
, such a scheme can be described by
It is assumed that 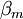 determines
determines 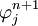 uniquely. Now, since the above equation represents a linear relationship between
uniquely. Now, since the above equation represents a linear relationship between 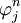 and
and 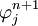 we can perform a linear transformation to obtain the following equivalent form,
we can perform a linear transformation to obtain the following equivalent form,
Theorem 1: Monotonicity preserving
The above scheme of equation (2) is monotonicity preserving if and only if
Proof - Godunov (1959)
Case 1: (sufficient condition)
Assume (3) applies and that 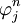 is monotonically increasing with
is monotonically increasing with 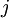 .
.
Then, because 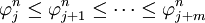 it therefore follows that
it therefore follows that 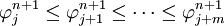 because
because
This means that monotonicity is preserved for this case.
Case 2: (necessary condition)
For the same monotonically increasing 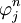 , assume that
, assume that 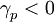 for some
for some 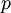 and choose
and choose
Then from equation (2) we get
Now choose 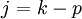 , to give
, to give
which implies that 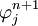 is NOT increasing, and we have a contradiction. Thus, monotonicity is NOT preserved for
is NOT increasing, and we have a contradiction. Thus, monotonicity is NOT preserved for 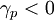 , which completes the proof.
, which completes the proof.
Theorem 2: Godunov’s Order Barrier Theorem
Linear one-step second-order accurate numerical schemes for the convection equation
cannot be monotonicity preserving unless
where 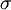 is the signed Courant–Friedrichs–Lewy condition (CFL) number.
is the signed Courant–Friedrichs–Lewy condition (CFL) number.
Proof - Godunov (1959)
Assume a numerical scheme of the form described by equation (2) and choose
The exact solution is
If we assume the scheme to be at least second-order accurate, it should produce the following solution exactly
Substituting into equation (2) gives:
Suppose that the scheme IS monotonicity preserving, then according to the theorem 1 above, 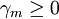 .
.
Now, it is clear from equation (15) that
Assume  and choose
and choose 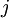 such that
such that 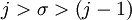 . This implies that
. This implies that 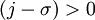 and
and 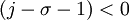 .
.
It therefore follows that,
which contradicts equation (16) and completes the proof.
The exceptional situation whereby 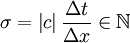 is only of theoretical interest, since this cannot be realised with variable coefficients. Also, integer CFL numbers greater than unity would not be feasible for practical problems.
is only of theoretical interest, since this cannot be realised with variable coefficients. Also, integer CFL numbers greater than unity would not be feasible for practical problems.
See also
References
- Godunov, Sergei K. (1954), Ph.D. Dissertation: Different Methods for Shock Waves, Moscow State University.
- Godunov, Sergei K. (1959), A Difference Scheme for Numerical Solution of Discontinuous Solution of Hydrodynamic Equations, Math. Sbornik, 47, 271-306, translated US Joint Publ. Res. Service, JPRS 7226, 1969.
- Wesseling, Pieter (2001), Principles of Computational Fluid Dynamics, Springer-Verlag.
Further reading
- Hirsch, C. (1990), Numerical Computation of Internal and External Flows, vol 2, Wiley.
- Laney, Culbert B. (1998), Computational Gas Dynamics, Cambridge University Press.
- Toro, E. F. (1999), Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer-Verlag.
- Tannehill, John C., et al., (1997), Computational Fluid mechanics and Heat Transfer, 2nd Ed., Taylor and Francis.

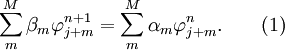
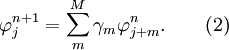
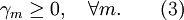
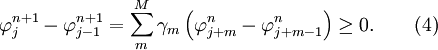
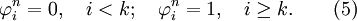
![\varphi _j^{n + 1} - \varphi _{j-1}^{n+1} = \sum\limits_m^M {\gamma _m } \left( {\varphi _{j + m}^{n} - \varphi _{j + m - 1}^{n} } \right) = \left\{ {\begin{array}{*{20}c}
{0,} & {\left[ {j + m \ne k} \right]} \\
{\gamma _m ,} & {\left[ {j + m = k} \right]} \\
\end{array}} \right . \quad \quad ( 6)](/W/images/math/c/e/0/ce0ac9e056c71c1d352f261c85678589.png)