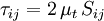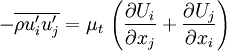Two equation turbulence models
From CFD-Wiki
| Line 1: | Line 1: | ||
| - | Two | + | Two equation turbulence models are one of the most common type of turbulence models. Models like the [[K-epsilon models|k-epsilon model]] and the [[K-omega models|k-omega model]] have become industry standard models and are commonly used for most types of engineering problems. Two equation turbulence models are also very much still an active area of research and new refined two-equation models are still being developed. |
| - | By definition, two | + | By definition, two equation models include two extra transport equations to represent the turbulent properties of the flow. This allows a two equation model to account for history effects like convection and diffusion of turbulent energy. |
Most often one of the transported variables is the [[Turbulent kinetic energy|turbulent kinetic energy]], <math>k</math>. The second transported variable varies depending on what type of two-equation model it is. Common choices are the turbulent [[Dissipation|dissipation]], <math>\epsilon</math>, or the [[Specific dissipation|specific dissipation]], <math>\omega</math>. The second variable can be thought of as the variable that determines the scale of the turbulence (length-scale or time-scale), whereas the first variable, <math>k</math>, determines the energy in the turbulence. | Most often one of the transported variables is the [[Turbulent kinetic energy|turbulent kinetic energy]], <math>k</math>. The second transported variable varies depending on what type of two-equation model it is. Common choices are the turbulent [[Dissipation|dissipation]], <math>\epsilon</math>, or the [[Specific dissipation|specific dissipation]], <math>\omega</math>. The second variable can be thought of as the variable that determines the scale of the turbulence (length-scale or time-scale), whereas the first variable, <math>k</math>, determines the energy in the turbulence. | ||
| - | The basis for all two | + | ==Boussinesq eddy viscosity assumption== |
| + | |||
| + | The basis for all two equation models is the [[Boussinesq eddy viscosity assumption]], which postulates that the [[Reynolds stress tensor]], <math>\tau_{ij}</math>, is proportional to the mean strain rate tensor, <math>S_{ij}</math>, and can be written in the following way: | ||
:<math>\tau_{ij} = 2 \, \mu_t \, S_{ij}</math> | :<math>\tau_{ij} = 2 \, \mu_t \, S_{ij}</math> | ||
| Line 13: | Line 15: | ||
:<math> -\overline{\rho u'_i u'_j} = \mu_t \, \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} \right)</math> | :<math> -\overline{\rho u'_i u'_j} = \mu_t \, \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} \right)</math> | ||
| - | The Boussinesq assumption is both the strength and the weakness of two equation models. This assumption is a huge simplification which allows one to think of the effect of turbulence on the mean flow in the same way as molecular viscosity affects a laminar flow. The assumption also makes it possible to introduce intuitive scalar turbulence variables like the turbulent energy and dissipation and to relate these variables to even more intuitive variables like [[Turbulence intensity|turbulence intensity]] and [[Turbulence length scale|turbulence length scale]]. | + | Normally the eddy viscosity, <math>\mu_t</math>, is computed from the two transported turbulence variables. |
| + | |||
| + | The Boussinesq assumption is both the strength and the weakness of two equation models. This assumption is a huge simplification which allows one to think of the effect of turbulence on the mean flow in the same way as molecular viscosity affects a laminar flow. The assumption also makes it possible to introduce intuitive scalar turbulence variables like the turbulent energy and dissipation and to relate these variables to even more intuitive variables like [[Turbulence intensity|turbulence intensity]] and [[Turbulence length scale|turbulence length scale]]. The weakness of the Boussinesq assumption is that it is not in general valid. There is nothing which says that the Reynolds stress tensor must be proportional to the strain rate tensor. In complex flows, like flows with strong curvature, this is not valid either. This give two equation models inherent problems to predict strongly rotating flows and other flows where curvature effects are significant. | ||
| + | |||
{{stub}} | {{stub}} | ||
Revision as of 21:15, 9 May 2006
Two equation turbulence models are one of the most common type of turbulence models. Models like the k-epsilon model and the k-omega model have become industry standard models and are commonly used for most types of engineering problems. Two equation turbulence models are also very much still an active area of research and new refined two-equation models are still being developed.
By definition, two equation models include two extra transport equations to represent the turbulent properties of the flow. This allows a two equation model to account for history effects like convection and diffusion of turbulent energy.
Most often one of the transported variables is the turbulent kinetic energy, 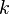 . The second transported variable varies depending on what type of two-equation model it is. Common choices are the turbulent dissipation,
. The second transported variable varies depending on what type of two-equation model it is. Common choices are the turbulent dissipation,  , or the specific dissipation,
, or the specific dissipation, 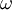 . The second variable can be thought of as the variable that determines the scale of the turbulence (length-scale or time-scale), whereas the first variable,
. The second variable can be thought of as the variable that determines the scale of the turbulence (length-scale or time-scale), whereas the first variable, 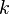 , determines the energy in the turbulence.
, determines the energy in the turbulence.
Boussinesq eddy viscosity assumption
The basis for all two equation models is the Boussinesq eddy viscosity assumption, which postulates that the Reynolds stress tensor, 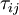 , is proportional to the mean strain rate tensor,
, is proportional to the mean strain rate tensor, 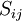 , and can be written in the following way:
, and can be written in the following way:
Where 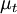 is a scalar property called the eddy viscosity. The same equation can be written more explicitly as:
is a scalar property called the eddy viscosity. The same equation can be written more explicitly as:
Normally the eddy viscosity, 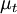 , is computed from the two transported turbulence variables.
, is computed from the two transported turbulence variables.
The Boussinesq assumption is both the strength and the weakness of two equation models. This assumption is a huge simplification which allows one to think of the effect of turbulence on the mean flow in the same way as molecular viscosity affects a laminar flow. The assumption also makes it possible to introduce intuitive scalar turbulence variables like the turbulent energy and dissipation and to relate these variables to even more intuitive variables like turbulence intensity and turbulence length scale. The weakness of the Boussinesq assumption is that it is not in general valid. There is nothing which says that the Reynolds stress tensor must be proportional to the strain rate tensor. In complex flows, like flows with strong curvature, this is not valid either. This give two equation models inherent problems to predict strongly rotating flows and other flows where curvature effects are significant.