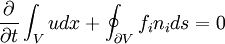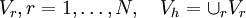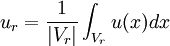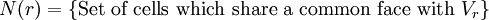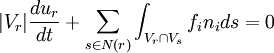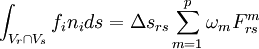Finite volume
From CFD-Wiki
The Finite Volume Method (FVM) is one of the most versatile discretization techniques used in CFD. Based on the control volume formulation of analytical fluid dynamics, the first step in the FVM is to divide the domain into a number of control volumes (aka cells, elements) where the variable of interest is located at the centroid of the control volume. The next step is to integrate the differential form of the governing equations (very similar to the control volume approach) over each control volume. Interpolation profiles are then assumed in order to describe the variation of the concerned variable between cell centroids. The resulting equation is called the discretized or discretization equation. In this manner, the discretization equation expresses the conservation principle for the variable inside the control volume.
The most compelling feature of the FVM is that the resulting solution satisfies the conservation of quantities such as mass, momentum, energy, and species. This is exactly satisfied for any control volume as well as for the whole computational domain and for any number of control volumes. Even a coarse grid solution exhibits exact integral balances.
FVM is the ideal method for computing discontinuous solutions arising in compressible flows. Any discontinuity must satisfy the Rankine-Hugoniot jump condition which is a consequence of conservation. Since finite volume methods are conservative they automatically satisfy the jump conditions and hence give physically correct weak solutions.
FVM is also preferred while solving partial differential equations containing discontinuous coefficients.
Integral form of conservation law
Consider a single partial differential equation in conservation form
where 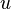 is a conserved quantity and
is a conserved quantity and
is the flux vector. Integrating this over any volume 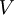 in
in 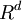 we get the integral form of the conservation law
we get the integral form of the conservation law
where the divergence theorem has been used to convert the divergence term to a surface integral over the surface 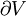 and
and 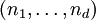 is the unit outward normal to
is the unit outward normal to 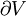 . The above equation is the starting point for the finite volume method.
. The above equation is the starting point for the finite volume method.
Finite volume formulation
The computational domain 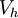 is divided into non-overlapping cells or finite volumes
is divided into non-overlapping cells or finite volumes
Usually these cells are polygons (triangles, quadrilaterals) in 2-D and polyhedra (tetrahedron, hexahedron, prims, etc) in 3-D.
Introduce the cell average value over the cell 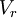
which is the basic unknown quantity in the finite volume method. Let
Then the integral conservation law for cell 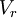 is
is
It now remains to approximate the flux integral. This can be achieved using gaussian quadrature. Taking 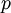 gaussian points we get
gaussian points we get
where 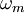 are the gaussian weights and
are the gaussian weights and 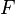 is an approximation to
is an approximation to 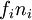 .
.
External links
- The Finite Volume Method (FVM) - An introduction by Oliver Rübenkönig of Albert Ludwigs University of Freiburg, available under the GNU Free Document License|GFDL.
Return to Numerical Methods

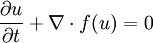
![f(u) = [ f_1(u), \ldots, f_d(u)]](/W/images/math/e/6/7/e671f66155b039e99a8afae464eb9888.png)