 |
|
|
[Sponsors] | |||||
How to set up a 2D Taylor-Couette case in FLUENT? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Magnus
Join Date: Feb 2020
Location: Norway
Posts: 5
Rep Power: 6  |
Hello fellow CFDers, I am quite new to FLUENT so any help would be greatly appreciated.
Problem description: I want to study the classic Taylor-Couette problem consisting of an annular fluid domain encased by two concentric cylinders, where the inner most cylinder is rotating while the outer most cylinder is stationary. See the attached image for reference Taylor_vortecies.png. As i want to study this problem using a 2D cross section of the concentric cylinders (z-r plane in the attatched image), I have encountered a problem with the boundary conditions for the rotating wall. I can not seem to find a way to give the rotating wall a speed in the theta (see attatch for ref) direction, i.e the normal direction of the crossectional 2D plane. I have tried to use the Axissymmetric option in FLUENT, but since the axis of rotations placement differs from the rotational wall placement. For example if you had a 100mm inner cylinder, the axis of rotation would lie in the middle of that cylinder, while the rotational wall would be the wall of that cylinder. FLUENT does not seem to like if this is the case. For 2D pipe flows this is not a problem since the axis of rotation is in the middle of the pipe. Thank you very much for reading. Any help is greatly appreciated! Best regards, Magnus |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
The only requirement Fluent has with respect to 2D cases is that the mesh should be in its x-y plane. It cannot be in any parallel plane either. So, z must be 0. Now, for concentric cylinders, their center point could be located anywhere, say, (10, 13.5). But the axis of rotation can only be (0, 0, 1). Rotation could be CW or CCW. What you need to provide correctly is the center point. Then it will work as expected.
Second thing, not related to Fluent or simulation, is Taylor-Couette Flow. Except for very low Re, flow is 3D, so, you would miss most of the features of the flow in a 2D case.
__________________
Regards, Vinerm PM to be used if and only if you do not want something to be shared publicly. PM is considered to be of the least priority. |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Magnus
Join Date: Feb 2020
Location: Norway
Posts: 5
Rep Power: 6  |
Quote:
Problem is that the axis of rotation must also be either x or y in my case, since i want to simulate a 2D case for the r-z plane (See the image below for ref.) CFD_example2_omega1.9_Re123.png Therefore i thought i would model it like this: CFDonline.png Where the line on the x axis is the axis of rotation and symmetry. And the rectangle above is the cross section of the cylinder, where the lower line is the moving cylinder wall. Thank you again! |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
|
That is not a possibility in 2D since the physics is no longer two-dimensional. Rotation around x-axis will make the case 3D because that would bring gradients in the
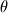 direction. So, the only viable solution is 3D. direction. So, the only viable solution is 3D.
__________________
Regards, Vinerm PM to be used if and only if you do not want something to be shared publicly. PM is considered to be of the least priority. |
|
|
|

|
|
|
|
|
#5 | |
|
New Member
Magnus
Join Date: Feb 2020
Location: Norway
Posts: 5
Rep Power: 6  |
Quote:
Do you have any suggestions on how to simulate this case without going to a full 3D case? The full 3D case will take a LOT of time to simulate, therefore it would be very helpfull to have a simpler case. Thanks Magnus |
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
|
I doubt if anyone has ever modeled TC flow in two-dimensions. It certainly is doable but not in standard coordinates; this would require transformation to different coordinates. Refer the following
https://rd.springer.com/article/10.1...65542509040162 What I can suggest is to model it in 3D but keep axial dimension confined to one cell (TC cell and not mesh cell) and apply translational periodicity on end faces of the cylinders.
__________________
Regards, Vinerm PM to be used if and only if you do not want something to be shared publicly. PM is considered to be of the least priority. |
|
|
|

|
|
 |
| Tags |
| boundary condition, rotating wall, taylor-couette |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| looking for a smart interface matlab fluent | chary | FLUENT | 24 | June 18, 2021 09:07 |
| [Commercial meshers] OpenFoam Mesh to Fluent Mesh in parallel case | DominicTNC | OpenFOAM Meshing & Mesh Conversion | 3 | November 22, 2017 09:19 |
| [snappyHexMesh] determining displacement for added points | CFDnewbie147 | OpenFOAM Meshing & Mesh Conversion | 1 | October 22, 2013 09:53 |
| Can't run a case in HelyxOS with an imported mesh from Fluent | HHOS | OpenFOAM Running, Solving & CFD | 0 | July 2, 2013 06:25 |
| How to show the transient case? | H.P.LIU | Phoenics | 7 | July 13, 2010 04:31 |