 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Jun 2010
Posts: 9
Rep Power: 16  |
Hello,
I am working the Re=3900 2-D cylinder problem for a turbulence class in graduate school. We were to use the k-e and k-w turbulence models and plot uu Reynolds stress profiles to compare to Kravchenko's paper. How do I back out the Reynolds stress components I need from the turbulent quantities given by these two models? I imagine I just use the Bouss Approx, and write a UDF to plot them, but I've never used the UDF's. Can someone give me some idiot-proof step by step instructions on how to do this? Thanks! |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Smith, John
Join Date: Nov 2010
Posts: 8
Rep Power: 15  |
i have the same question right now

|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Andre Novgorodcev
Join Date: Jan 2012
Posts: 3
Rep Power: 14  |
I'm facing the same problem right now.

|
|
|
|

|
|
|
|
|
#4 |
|
New Member
Join Date: Mar 2011
Posts: 7
Rep Power: 15  |
You have to use Bous. Approx.
Use the Define->Custom Field Functions to calculate delu=dx-velocity-dx + dy-velocity-dy + dz-velocity-dz then calculate strain rate tensor S_uu S_uu=dx-velocity-dx - 1 / 3 * dukxk Then use -u'u'=2*viscosity-turb*S_uu/density - 2/3*turb-kinetic-energy |
|
|
|

|
|
|
|
|
#5 | |
|
Super Moderator
|
Quote:
|
||
|
|

|
||
|
|
|
#6 | |
|
Member
Join Date: May 2013
Posts: 32
Rep Power: 13  |
Quote:
I need to define Reynolds stresses in fluent with k-e model. I also could not understand the term dukxk and you define in the beginning something called delu but you do not use it anywhere. could you explain what is that one also? Thank you very much, I really appreciate it. |
||
|
|

|
||
|
|
|
#7 |
|
New Member
Miloslav Dohnal
Join Date: Jan 2014
Location: Brno, The Czech Republic
Posts: 7
Rep Power: 12  |
Hello everyone
 Yesterday, I found this thread and spent almost whole day by searching for answer with some, let's say, proof or explanation. I found that the problem raises from the transport equation of k in two equation models; and it's one of the problems in turbulence modeling. In general, we have more unknowns to solve than available equations; and Boussinesq aproximation is used to enclose transport equation of k in one- or two- equation models. And now, back to problem: let's have the Boussinesq aproximation 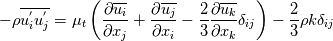 where 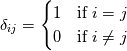 is Kronecker delta is Kronecker delta and also have those two vectors: position vector 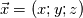 and velocity vector 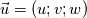 if the flow is incompressible, then 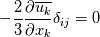 Now, it only depands what kind of Reynolds stress you want. For instance, if you want to know normal stress 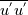 simply put simply put 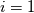 and and 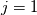 ; then, substitute first element in ; then, substitute first element in 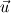 and and 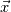 to the Boussinesq aproximation and do the math. You will obtain: to the Boussinesq aproximation and do the math. You will obtain: 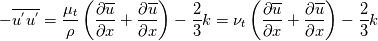 And if you want to know shear stress 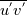 , just put , just put 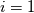 and and 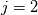 and you will get: and you will get: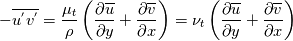 Apply same principle for any other Reynolds stress you want to know and just simply put this to Fluent using Custom Field Functions Reference Wilcox, D. C., 2006, Turbulence Modeling for CFD, 3rd ed., Dcw Industries, Incorporated. |
|
|
|

|
|
 |
| Tags |
| boussinesq, reynolds, stress |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Two questions on Fluent UDF | Steven | Fluent UDF and Scheme Programming | 7 | March 23, 2018 03:22 |
| Obtaining Reynolds Number in FLUENT | Emmanuel | FLUENT | 2 | April 7, 2016 01:46 |
| RMS velocity and reynolds stres with fluent | gina | FLUENT | 1 | May 20, 2013 04:05 |
| Reynolds stresses without velocity correlations? | Phil | Main CFD Forum | 1 | October 2, 2006 04:29 |
| Reynolds stresses and second law | JF | Main CFD Forum | 6 | June 2, 2005 22:57 |