 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Junaid Ahmad Khan
Join Date: Mar 2010
Location: Islamabad
Posts: 43
Rep Power: 16  |
HI to All,
I am trying to solve Lid Driven Cavity problem using Finite Volume Method, for that i want to use Simple Algorithm. I have all ready solve LDC using Artificial Compressibility now i want to use SIMPLE Algorithm to solve velocity-pressure coupling, for that i am following Versteeg's book. I am using steady navier stokes equations for LDC. The procedure that i have adopted is given below: 1. Initialize u*,v*,p* 2. Solve Discretised momentum equation and Calculated u*,v* NOW comes the problem. in step 3 when i try to calculate p'. 3. the equation is a[i,j]p'[i,j]=a[i-1,j]p'[i-1,j]+a[i+1,j]p'[i+1,j]+a[i,j-1]p'[i,j-1]+a[i,j+1]p'[i,j+1]+b'[i,j] a[i-1,j]=(d A)[i-1,j] a[i+1,j]=(d A)[i+1,j] a[i,j-1]=(d A)[i,j-1] a[i,j+1]=(d A)[i,j+1] b'[i,j] = (u*A)[i-1,j]-(u*A)[i+1,j]+(v*A)[i,j+1]-(v*A)[i,j-1] In this equation i need d to be calculated which is d=A/a where a is the centeral coefficient of velocity equation. where i try to calculate this it some how a become zero which makes d=infinity. and p' become undefined or infinity. that cause problems in step 4 i.e. 4. p[i,j]=p*[i,j]+p'[i,j] u[i,j]=u*[i,j]+d[i,j]*(p'[i-1,j]-p'[i,j]) u[i,j]=u[i,j]+u[i,j]*(p'[i,j-1]-p'[i,j]) 5. Set Boundary condition for u and v 6. Set Wall presure gradient to zero 7. Copy Values p*=p u*=u v*=v 8. Check Convergence. and goto Step 1 My main problem is step 3 any sugesstions for that? (I am using c++) Regards Junaid |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Join Date: Aug 2011
Posts: 272
Rep Power: 15  |
Quote:
I do not know how you defined your notations but your implementation is a bit weird. You should rather have something like: ap[i,j]p'[i,j]=aw[i,j]p'[i-1,j]+ae[i,j]p'[i+1,j]+as[i,j]p'[i,j-1]+an[i,j]p'[i,j+1]+b'[i,j] |
||
|
|

|
||
|
|
|
#3 |
|
Member
Junaid Ahmad Khan
Join Date: Mar 2010
Location: Islamabad
Posts: 43
Rep Power: 16  |
Yes your are correct yours make more sense. Mine your are same.
So any thoughts how to calculate d |
|
|
|

|
|
|
|
|
#4 |
|
Member
Michail
Join Date: Apr 2009
Location: Lithuania
Posts: 41
Rep Power: 17  |
Hi Junaid Ahmad!
Take a look here http://www.cfd-online.com/Wiki/Sampl...9_-_Fortran_90 Hope this will help Last edited by Michail; August 13, 2012 at 01:17. |
|
|
|

|
|
|
|
|
#5 |
|
Member
Junaid Ahmad Khan
Join Date: Mar 2010
Location: Islamabad
Posts: 43
Rep Power: 16  |
This is Pressure Correction File. First let me tell you that i have no working knowledge of FORTRAN So its hard for me to understand this. If I am not wrong then its your code. it will be very help full if you explain it and tell me which book you follow to develop your understanding. Or at least explain the Highlighted terms in this code.
Regards Junaid !************************************************* ********************* Subroutine Solve_Pressure_Correction include 'icomm_1.f90' DpU(2:NXmax,2:NYmax) = 1./Ap(2:NXmax,2:NYmax,1) DpV(2:NXmax,2:NYmax) = 1./Ap(2:NXmax,2:NYmax,2) !************************************************* *************************************** ! vertical faces East - e Do 101 I=1,NXmax Do 101 J=1,NYmax-1 If((i.ne.1).and.(i.ne.NXmax))then DXc_e = Xc(i+1,j+1) - Xc(i,j+1) S_e = Y(i ,j+1) - Y(i,j ) VOL_e = DXc_e * S_e !------------------------------------------------------------- APU_e = 0.5 * ( DpU(i,j+1) + DpU(i+1,j+1) ) Ul_e = 0.5 * ( F(i,j+1,1) + F(i+1,j+1,1) ) DPl_e = 0.5 * ( DPx_c(i,j+1) + DPx_c(i+1,j+1) ) DPx_e = ( F(i+1,j+1,4) - F(i,j+1,4) ) / DXc_e U_e = Ul_e + APU_e * VOL_e * ( DPl_e - DPx_e) !-------------------------------------------------------------- Con_e(i,j) = U_e * S_e End If Con_e(1,j) = 0. Con_e(NXmax,j) = 0. 101 continue !************************************************* *************************************** ! horisontal faces Do 102 I=1,NXmax-1 Do 102 J=1,NYmax If((j.ne.1).and.(j.ne.NYmax))then DYc_n = Yc(i+1,j+1) - Yc(i+1,j) S_n = X(i+1,j ) - X(i ,j) VOL_n = DYc_n * S_n !----------------------------------------------------------- APV_n = 0.5 * ( DpV(i+1,j) + DpV(i+1,j+1) ) Vl_n = 0.5 * ( F(i+1,j,2) + F(i+1,j+1,2) ) DPl_n = 0.5 * ( DPy_c(i+1,j) + DPy_c(i+1,j+1) ) DPy_n = ( F(i+1,j+1,4) - F(i+1,j,4) ) / DYc_n V_n = Vl_n + APV_n * VOL_n * ( DPl_n - DPy_n ) !----------------------------------------------------------- Con_n(i,j) = V_n * S_n End If Con_n(i,1) = 0. Con_n(i,NYmax) = 0. 102 continue !************************************************* *************************************** Summ = 0. Do 200 I=2,NXmax Do 200 J=2,NYmax S_e = Y(i ,j) - Y(i,j-1) S_n = X(i ,j) - X(i-1,j) An(i,j) = 0.5 * ( DpV(i,j) + DpV(i,j+1) ) * S_n * S_n As(i,j) = 0.5 * ( DpV(i,j) + DpV(i,j-1) ) * S_n * S_n Ae(i,j) = 0.5 * ( DpU(i,j) + DpU(i+1,j) ) * S_e * S_e Aw(i,j) = 0.5 * ( DpU(i,j) + DpU(i-1,j) ) * S_e * S_e Ap(i,j,3) = (An(i,j) + As(i,j) + Ae(i,j) + Aw(i,j)) Sp(i,j,3) = -1. * ( Con_n(i-1,j) - Con_n(i-1,j-1) + Con_e(i,j-1) - Con_e(i-1,j-1) ) Summ = Summ + Sp(i,j,3) ! 200 continue write(*,*)'Sum',summ !************************************************* ********************************** !************************************************* ********************************** write(*,*) Summ write(*,*)'solve PP' niter = 0 20 call Convergence_Criteria(3,Res_sum_before) niter= niter + 1 Call TDMA_1(3) call Convergence_Criteria(3,Res_sum_After) If((abs(Res_sum_before-Res_sum_After).Ge.0.0000001).and.(niter.le.500).an d.(abs(Res_sum_After).ge.0.0001))go to 20 write(*,*)'Res_sum_before-Res_sum_After',Res_sum_before-Res_sum_After,niter !************************************************* ********************************** !************************************************* ********************************** ! velocities and pressure correction Do 300 I=2,NXmax Do 300 J=2,NYmax DY = Y(i,j)-Y(i,j-1) DX = X(i,j)-X(i-1,j) PPe = 0.5 * ( F(i,j,3) + F(i+1,j,3) ) PPw = 0.5 * ( F(i,j,3) + F(i-1,j,3) ) PPn = 0.5 * ( F(i,j,3) + F(i,j+1,3) ) PPs = 0.5 * ( F(i,j,3) + F(i,j-1,3) ) F(i,j,1) = F(i,j,1) + (PPw - PPe) * DpU(i,j) * Dy F(i,j,2) = F(i,j,2) + (PPs - PPn) * DpV(i,j) * Dx F(i,j,4) = F(i,j,4) + 0.1 * F(i,j,3) 300 continue !************************************************* ********************************** ! correct convective fluxes through vertical East faces Do 701 I=1,NXmax Do 701 J=1,NYmax-1 If((i.ne.1).and.(i.ne.NXmax))then Con_e(i,j) = Con_e(i,j) + Ae(i,j+1) * (F(i+1,j+1,3)-F(i,j+1,3) ) end if if((i.eq.1).or.(i.eq.NXmax))Con_e(i,j)=0. 701 continue ! correct convective fluxes through horisontal North faces Do 702 I=1,NXmax-1 Do 702 J=1,NYmax If((j.ne.1).and.(j.ne.NYmax))then Con_n(i,j) = Con_n(i,j) + An(i+1,j) * (F(i+1,j+1,3)-F(i+1,j,3) ) end if if((j.eq.1).or.(j.eq.NYmax))Con_n(i,j)=0. 702 continue !************************************************* ********************************** Do 501 I=1,NXmaxC F(i,1,4) = F(i,2,4) ! F(i,NYmaxC,4) = F(i,NYmaxC-1,4)! 501 continue Do 502 J=1,NYmaxC F(1,j,4) = F(2,j,4) ! F(NXmaxC,j,4) = F(NXmaxC-1,j,4) ! 502 continue F(:,:,4) = F(:,:,4) - F(3,4,4) !************************************************* ********************************** Return End |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Join Date: Aug 2011
Posts: 272
Rep Power: 15  |
Hi Junaid,
The code of Michail is really well writen and the notations are very understanable because intuitive. Greatings for him !! You should first read a book on finite volume method and SIMPLE like the ones of Patankar, Peric or Versteek. The one of Peric should be better because Michail used colocated variables arrangement based on Rhie and Chow interpolation. So for this purpose I think Peric's book is better oriented. However just reading the code of Michail you understand what he is talking about... Quote:
Really get a book on FV , SIMPLE algorithm with Rhie and Chow interpolation and everything will be clear for you because the code is really clear!! |
||
|
|

|
||
|
|
|
#7 |
|
Member
Junaid Ahmad Khan
Join Date: Mar 2010
Location: Islamabad
Posts: 43
Rep Power: 16  |
Thanks,
I am following verseek's book, and in it d(i-1,j)=A(i-1,j)/ap(i-1,j) A(i-1,j) is area of west face ap(i-1,j) is central coefficient of velocity the problem is when i calculate ap by use the value of u* and v* and use it to find p' it some how blow up the velocity field, and when i use that to calculate ap which is ap = aw+ae+an+as+dF For Hybrid scheme in that e.g. ae=Max(De-Fe/2,-Fe,0) and Fe=0.5*(uP+uE) De=Gama if dx=dy so when velocity blowup everything went side ways. So what should i use when i calculate ap do i use u* or u the corrected velocity. Anyways i try to find this book of Peric and see how it works. |
|
|
|

|
|
|
|
|
#8 |
|
Member
Michail
Join Date: Apr 2009
Location: Lithuania
Posts: 41
Rep Power: 17  |
Dear Leflix
May I'll include Your explanations into the code? I guess it'l be better for future? Regards Michail F(:,:,1) - U-velocity F(:,:,2) - V-velocity F(:,:,3) - pressure correction F(:,:,4) - pressure |
|
|
|

|
|
|
|
|
#10 |
|
Member
Michael Moor
Join Date: May 2012
Location: Ireland
Posts: 30
Rep Power: 13  |
I have a working Poiseulle flow problem based on Versteeg which matches nicely to the Hagen-Poiseulle velocity profile. It is extremey well annotated and culd be of great help.
It has under-relaxation and uses the JAcobi method, and was possible due to members of this forum such as Ztdep and houkensjtu. The only problems that i have, are that the momentum resuduals do not get much better that 1e-3, and that the largest mesh that i am able to solve for (without divergence or stagnation) is about 34*34.... I would greatly appreciate any help, but for right now, you can look at my code... Regards, Michael |
|
|
|

|
|
|
|
|
#11 |
|
Member
Junaid Ahmad Khan
Join Date: Mar 2010
Location: Islamabad
Posts: 43
Rep Power: 16  |
If you implemented versteeks method then would realy like to take a look at it. you may give me the like of send me the code at tojunaidahmad@hotmail.com
Regards Junaid |
|
|
|

|
|
|
|
|
#12 |
|
Member
Michail
Join Date: Apr 2009
Location: Lithuania
Posts: 41
Rep Power: 17  |
Dear Junaid
I offer to take a look through M.Peric codes ftp://ftp.springer.de/pub/technik/peric/ There are both staggered and collocated grids codes for SIMPLE-algorithm. As concerned M.Peric book I offer to check torrents and previous posts on CFD-online. Fight for CFD and CFD will fight for You  Best wishes Michail Last edited by Michail; August 15, 2012 at 13:36. |
|
|
|

|
|
|
|
|
#13 |
|
Member
Junaid Ahmad Khan
Join Date: Mar 2010
Location: Islamabad
Posts: 43
Rep Power: 16  |
Thanks Michail, i need to know what is the best time to add under relaxation factor in the calculation of p, u, and v. now when i revisit the literature i find out that it is the under relaxation factor that cause divergence to me solution.
Regards Junaid |
|
|
|

|
|
|
|
|
#14 |
|
Member
Michael Moor
Join Date: May 2012
Location: Ireland
Posts: 30
Rep Power: 13  |
were you using implicit under-relaxation for u and v? what values were you using for under-relaxation to make it diverge? I am having a similar issue...
|
|
|
|

|
|
|
|
|
#15 |
|
Member
Junaid Ahmad Khan
Join Date: Mar 2010
Location: Islamabad
Posts: 43
Rep Power: 16  |
what is the good method for under relaxation do i use
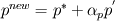 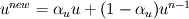  or use URF embedded in the discretised momentum equation Regards Junaid Last edited by JunaidAhmad; August 16, 2012 at 16:04. |
|
|
|

|
|
|
|
|
#16 | |
|
Member
Michael Moor
Join Date: May 2012
Location: Ireland
Posts: 30
Rep Power: 13  |
Quote:
AS for pressure under-relaxation, I understand it such that only the correction is under-relaxed... i.e. pnew = p* +alphap*p' |
||
|
|

|
||
|
|
|
#17 |
|
Member
Junaid Ahmad Khan
Join Date: Mar 2010
Location: Islamabad
Posts: 43
Rep Power: 16  |
I don't understand i did exactly what is written in book. it didn't work. I did the same think using artificial compressibility and it worked but using SIMPLE method it did not. the only thing left for me is to paste the code a let you guys decide what is wrong with it.
But first i have to go through one more time. |
|
|
|

|
|
|
|
|
#18 |
|
Member
Michael Moor
Join Date: May 2012
Location: Ireland
Posts: 30
Rep Power: 13  |
||
|
|

|
|
|
|
|
#19 |
|
Member
Junaid Ahmad Khan
Join Date: Mar 2010
Location: Islamabad
Posts: 43
Rep Power: 16  |
Yes i got the code . and its approach and mine is the same i.e. hi-bride scheme.
why we need SIMPLE Algorithm when We have Artificial compressibility? 
|
|
|
|

|
|
|
|
|
#20 |
|
Member
Michael Moor
Join Date: May 2012
Location: Ireland
Posts: 30
Rep Power: 13  |
||
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Finite Volume -- SIMPLE Algorithm | Roger | Main CFD Forum | 9 | September 25, 2023 12:04 |
| SIMPLE algorithm in 3D cylindrical coordinates | zouchu | Main CFD Forum | 1 | January 20, 2014 17:02 |
| SIMPLE algorithm confusion | lost.identity | Main CFD Forum | 1 | October 7, 2010 11:48 |
| SIMPLE OR SIMPLER algorithm | Sergio Costa | Main CFD Forum | 2 | July 29, 2007 06:44 |
| About Phase Coupled SIMPLE (PC-SIMPLE) algorithm | Yan Kai | Main CFD Forum | 0 | April 18, 2007 03:48 |