 |
|
|
[Sponsors] | |||||
Spalart-Allmaras and "Non-Conservative Diffusion" |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Peter Doings
Join Date: Sep 2012
Location: Portugal
Posts: 4
Rep Power: 13  |
Hello.
I'm an undergrad student and I'm implementing the S-A model for incompressible flow in a FV solver; I have access to STAR-CCM+'s documentation and there I found an entry explaining that they did not discretize explicitly one of parcels of the diffusion term but that they combined it with the conservative diffusion one. I tried to get to the formula on my own using the identity: 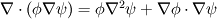 And got a very similar result to STAR's: ![\frac{1}{\sigma_\nu}[\int_S(\nu+\tilde{\nu})\nabla\nu \cdot dS + \int_V C_{b2} (\nabla \nu \cdot \nabla \nu)dV] \frac{1}{\sigma_\nu}[\int_S(\nu+\tilde{\nu})\nabla\nu \cdot dS + \int_V C_{b2} (\nabla \nu \cdot \nabla \nu)dV]](/Forums/vbLatex/img/b32a9e45dfd99838353fc48a0cc7112b-1.gif) 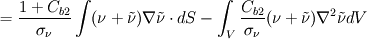 Except that in the documentation it appears as a 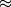 and the last term has, instead of the Laplacian, a and the last term has, instead of the Laplacian, a 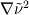 which I assume is their mistake (is it?). which I assume is their mistake (is it?).My questions are: a) is this common practice? and b) I'll treat the first term as a regular diffusion term with the diffusivity given by last iteration's 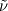 , but how can I best discretize the last one? Explicitly calculate the laplacian on a cell by cell basis, multiply by , but how can I best discretize the last one? Explicitly calculate the laplacian on a cell by cell basis, multiply by 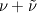 and put the result in the right-hand side? and put the result in the right-hand side?Any help apreciated. |
|
|
|

|
|
 |
|
|