 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Nov 2014
Posts: 1
Rep Power: 0  |
Hi
I am new to this forum and very much new to CFD, I have used commercial codes in the past but have never really delved into the theory until now. I have been set at university a lab to convert a 1-D Convection Diffusion problem into matrix form within Excel. I am using finite difference schemes to approximate the derivatives to the problem. I am using a central difference scheme to approximate the diffusion term and a first order upwind approximation for the convection term. The governing equation is 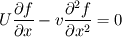 Boundary conditions - f=0 at x=0 and f=1 at x=L My problem is, I have created the matrices of these terms and completed a combined coefficient matrix and my task is to comment on accuracy, stability when varying the Peclet number. Beyond that I also have to modify the convection scheme from the first order upwind scheme to a second-order central difference scheme and compare. So First Order Upwind Scheme 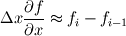 Modified to Second Order Central Difference 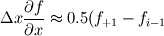 These are constructed into a 11x11 matrix following the discretised form of the equation. This is just [Pe(Delta(x))*AConv+Adiff]*F = B The matrices bar the convection matrix are pretty irrelevant to my question so with relation to the convection upwind scheme equation used above it is easy and is just 1's down the central diagonal apart from the corners for boundary conditions and the diagonal below is just -1's. Everything else is 0. I'm just wondering for the conversion of this matrix to a second-order central difference, how should the matrix look. I know it will be 0's instead of 1's down the central diagonal but the 0.5? I am getting very erratic results for different Peclet numbers with the second order central difference implementation I have tried so I'm thinking I have entered the matrix in wrong. Sorry if this is a little confusing, I can attempt to share my spread sheet if required. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
Could you share your solution for different Peclet numbers? Say, from 0.5 to 4 with steps 0.5?
How do you expect the solutions to behave at the different Peclet numbers and why? |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| problem with diffusion | katya | FLUENT | 1 | March 29, 2016 16:07 |
| How to solve natural convection problem in fluent? | samantasubho | FLUENT | 7 | April 17, 2014 02:07 |
| Is there a template for this problem (convection)? | massive_turbulence | OpenFOAM Programming & Development | 1 | May 25, 2013 03:55 |
| Heat sink with forced convection problem | Prasad | FLUENT | 5 | December 20, 2011 01:10 |
| Natural Convection Problem - Helium | marzoa | STAR-CCM+ | 0 | April 18, 2011 14:12 |