 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Guest
Posts: n/a
|
Hey,
1. What is the physical interpretation of the pressure in an incompressible fluid? 2. It seems to me that if we are solving the momentum equations explicitly in an incompressible fluid, then we use the pressure-velocity coupling to ensure that we actually are solving the problem implicitly (which sounds correct). Do we actually need the pressure to make this implicit coupling of the velocities in the domain? |
|

|
||
|
|
|
#2 |
|
Guest
Posts: n/a
|
There's always the option of using the sream function / vorticity formulation (for 1 or 2-d problems with constant viscosity). An extension of that with further manipulation gives a biharmonic equation for the stream function alone (with the same restrictions).
In either case the pressure is eliminated from the calculation - although a pressure field can be retrieved from the stream function solution. |
|

|
||
|
|
|
#3 |
|
Guest
Posts: n/a
|
the disavantages of stream function vorticity include, but not limited to:
6 components in 3d, while 4 components in 3d for velocity-pressure; vorticty is the derivative of velocity, so it demands more smoothness |
|

|
||
|
|
|
#4 |
|
Guest
Posts: n/a
|
physical interpretation of the pressure in incompressible flows?
pressure is just the pressure, the normal-direction force per area acting on the surfaces you are interested in. nothing fancy for the pressure in incompressible flows, in terms of concept. however, the propagation of the pressure in the incompressible flows is at an infinite speed. when you want to consider the hydroacoutsics, this is not the case (the speed of sound in water is more than 1000m/s, i don't remember exactly), but otherwise it is. in air, the propagation of pressure is the speed of the sound in air. that "the pressure progagate at infinite speed" equates a tiny chnage in the density can have a consequence of big change in pressure field. this is called stiffness. i don't understand your second question, so her i just say something i know. the role of pressure in incompressible flows is a lagrangian multiplier, which means the pressure demands the velocity field you obtained (with the moving the pressure to the right-hand-side of momentum equations) satify the conservation of mass. with pressure on the right hand side, where the pressure can be obtained by the approximation from the previous time step, you can get a velocity field. but you can a lot of, as a matter of fact infinite number of, velocity fields. however, such a field must satisfy the continuity equation. in penalty formulation, you can incorporate the continuity equation into the momentum equation & kind of limintate the pressure. so, you can work out the velocity field alone. penalty formulation reflects the epcicenter of "lagrangian multiplier" literatelly, but it is a bad approach and i surely suggest you not go for it. in compressible flows, the navier-stokes flows are solved in a mixed formulation, which simply means the most natural approach. unfornulately, at low sonic speed, the stiffness issue occurs and the mixed approaches does very poorly. you may use artificail compressibility or pressure stabilization methods, to try to extend the "mixed formulation"-which is excellent for compressibel flows & compressible elasticity to the incompressible limit. unfortunately, the extension is not successful, either due to implemental complexibity or performance/speed or both. so, the best category of handling incompressible flows is the splitting. and there are 3 categories for this business: 1. continuous splitting: you can derive a pressure poisson equation from the momentum and continuity, in a continuous sense; and impose boundary a neumann boundary condition for the pressure poisson; the boundary condition can be derived from application of momentum equation on the normal direction of the boundary. this approach is a little pain at the beginning, due to the boundary condtion; but once you have then ready, it's easy to proceed; 2. discrete splitting: you can continue the "mixed formulation" or the natural formulation, and get all matrices; then you do some manipulations to get a sub systems for the velocity and a pressure-poisson-like subsystem for the pressure. this apporach share a lot with the mixed formulation, so that it's easy to communicate with traditional compressible slovers. unfortunately, you still need add additonal boundary conditions onto matrices you just got. the reason, after you convert the matrices you just got into subsytems for the velocity and pressure, some information may get inactive, even the conversion is a one-on-one conversion. there are other types of discrete splitting, such as the one presented in the famous paper published in 1965 on "physics of fluids", in which this technqiue, finite volume method, staggered grid, and MAC free-surface capturing technique can be found (in one single paper -- can we find this kind of highly original papers now?) 3. semi-discrete approach this is simply the famous "fractional step" or "projection" by Chorin. I don't the "velocity correction" approach implemented in "Fluent" belongs to which category, such as SIMPLE, SIMPLER, and so on. but the procedures being used by commercial software must be good, which is not necessary a case for those published on journa papers. |
|

|
||
|
|
|
#5 |
|
Guest
Posts: n/a
|
a little calrification:
suppose we onvert system A to system B, in a one-on-one manner. we might think: since these two systems are equivalent to each other, solving B is the same as soliving A. unfortunately, this is a wrong idea. system B indeed equates system A, they contain the same information; however, some information may hide inside the system and simply can't be utilized. in other words, some information stored in system A may become intrinsic in B. as a consequence, we can't solve B and get the correct results. |
|

|
||
|
|
|
#6 |
|
Guest
Posts: n/a
|
"pressure is just the pressure, the normal-direction force per area acting on the surfaces you are interested in. nothing fancy for the pressure in incompressible flows, in terms of concept. "
I'm a bit confused here, let me reformulate my first question: Do we have some pressure acting in the incompressible system other than the dynamic pressure? |
|

|
||
|
|
|
#7 |
|
Guest
Posts: n/a
|
You have the static pressure, but in terms of the solution of the equations all that is important is the pressure gradient. You can add or subtract a gauge pressure from the flo field and get the same velocity field.
|
|

|
||
|
|
|
#8 |
|
Guest
Posts: n/a
|
Is it possible to eliminate the pressure term (by say assuming p = 0.5*rho*u≤) and do a least-squares fit to the resulting two equations (x-momentum and continuity) in a 1d problem?
|
|

|
||
|
|
|
#9 |
|
Guest
Posts: n/a
|
Yes. So what is the pressure gradient in an incompressible fluid? I understand that it resolves from the solution of the equations but is there a physical meaning behind it?
|
|

|
||
|
|
|
#10 |
|
Guest
Posts: n/a
|
In the incompressible equations the pressure (usually referred to as the dynamic pressure to distinguish it from the thermodynamic one) is the internal force required maintain mass conservation (which also prevents cavitation). Basically it describes the coupling between the momentum equation and the continuity equation;i.e. it's the force required to ensure that the velocity evolves in a manner that conserves mass (strictly speaking it's volume in the incompressible equations). If you know about classical mechanics (Lagrange & Hamilton) then in an inviscid fluid the pressure (p) is the "Lagrange multiply" that multiplies the mass-conservation constraint when added to the Lagrangian -variations with respect to p gives the mass conservation equation while variation of the other parameters yields the momentum equations.
|
|

|
||
|
|
|
#11 |
|
Guest
Posts: n/a
|
The interpretation of the pressure in incompressible flow as a Lagrange multiplier is the result of a particular mathematical analysis of NSE. If the equations are rewritten in the stream function-vorticity form or the stream function form, there is no pressure in the problem. The incompressible velocity field exists and can be computed without regard to the pressure. The incompressibility/mass conservation is being maintained without reference to a pressure. Where is a Lagrange multiplier in this case? If one expands the velocity field in terms of a divergence-free basis, the expansion will always be divergence-free no matter what expansion coefficients are chosen. If the expansion coefficients are chosen to best approximate the solution to the NSE, this solution will be divergence-free without regard to the pressure. The incompressibility condition acts like a conservation law. The "pressure" derived from the velocity field (say by the pressure Poisson equation) is that pressure-like quantity consistent with the flow field. How can we say that the pressure drives incompressible flow if there is no pressure appearing in the governing equation? Incompressibility drives the flow and pressure responds!
|
|

|
||
|
|
|
#12 |
|
Guest
Posts: n/a
|
"The interpretation of the pressure in incompressible flow as a Lagrange multiplier is the result of a particular mathematical analysis of NSE."
No - it follows from the derivation of the inviscid equations using a Lagrangian. This is also true for compressible flows! The streamfunction is the mathematical device. It's just a way of hiding the pressure, just like using the vorticity form in the 3D problem. "The incompressibility condition acts like a conservation law." No - it behaves as a constraint on the flow. The pressure is gradient is the force required to enforce the constraint. The constraint actually corresponds to the conservation of volume not mass (unless density is constant). Sara, If you're OK with the (thermodynamics) pressure in the compressible equations then one way of understanding the corresponding term in the incompressible equations is to nondimensionalize the compressible equations and perform a low Mach number asymptotic expansion of the equations. There are many examples of this procedure in papers within the Journal of Fluid mechanics. |
|

|
||
|
|
|
#13 |
|
Guest
Posts: n/a
|
Excellent answer Jonas, thank you, this was the essence of my confusion.
|
|

|
||
|
|
|
#14 |
|
Guest
Posts: n/a
|
No No No The confusion,if there is any, is the result of the definition of pressure in the mechanical sense, i.e., the normal component of force ..etc. The Kinetic theory of Gases gives the definition of pressure as the momentum exchange between the molecules or between the molecules and solid boundaries. in other words, it is another thermodynamic property of matter. If you adopt this definition then there will be a pressure whether we treat the flow as incompressible or compressible or whatever. It is a property of matter. Good Luck.
|
|

|
||
|
|
|
#15 |
|
Guest
Posts: n/a
|
But the original question was about INCOMPRESSIBLE flow.
|
|

|
||
|
|
|
#16 |
|
Guest
Posts: n/a
|
i suggest you not to try these kinds of approaches.
in fundamenatal and long-standing things, it's better to use something popular; once you reach to the front of the research field, try hard something unconventional |
|

|
||
|
|
|
#17 |
|
New Member
john mckelliget
Join Date: Mar 2009
Posts: 7
Rep Power: 17  |
The original question was about the PHYSICAL interpretation of pressure, so forget Lagrange multipliers.
Suppose you have a fluid completely at rest. The molecules are moving at high speed with random thermal motion. The molecules collide either with a real surface, or with the molecules on the other side of an imaginary surface. The average of these forces of collision give a normal force (the tangential forces cancel statistically) called the pressure. Now, if there is a velocity gradient the tangential forces do not quite cancel and a normal and a shear force are exerted on the surface. The normal force is called pressure and the tangential force is called viscosity. Incompressible or compressible - same thing Last edited by jwm; March 16, 2009 at 08:45. |
|
|
|

|
|
|
|
|
#18 |
|
Senior Member
Jonas T. Holdeman, Jr.
Join Date: Mar 2009
Location: Knoxville, Tennessee
Posts: 128
Rep Power: 18  |
No, John M, the question was
"1. What is the physical interpretation of the pressure in an incompressible fluid?" The key word here is "incompressible." We must distinguish between "incompressible flow" (a property of real fluids) and an "incompressible fluid" (which is an idealized concept). The incompressible fluid provides a model for incompressible flow. Being a concept, we do not have access to an incompressible fluid to experiment with and experimentally infer its properties. The closest thing in nature to an incompressible fluid might be the core of a neutron star, but we don't have access to that. So we must be careful of applying intuition, and examine the fluid from its mathematical description. There are (at least) two time (and spacial) scales associated with a real fluid, one associated with the speed of the fluid  and one associated with the speed of sound c(pressure variations) in the fluid. We may charactize the relation between these two by the Mach number and one associated with the speed of sound c(pressure variations) in the fluid. We may charactize the relation between these two by the Mach number 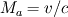 . For very small Mach number the nonstationary equations become stiff and computations become difficult. Taking the limit as . For very small Mach number the nonstationary equations become stiff and computations become difficult. Taking the limit as 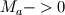 eliminates one of these scales giving the incompressible NSE and better-conditioned computations, but at a price. eliminates one of these scales giving the incompressible NSE and better-conditioned computations, but at a price. If we expand the density  , pressure , pressure 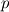 and velocity and velocity  in powers of in powers of 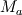 and collect terms with the same power, we find that to lowest order, the pressure appearing in the momentum equation (which is now the incompressible NSE) is the coefficient of and collect terms with the same power, we find that to lowest order, the pressure appearing in the momentum equation (which is now the incompressible NSE) is the coefficient of 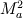 , two orders higher than the density or velocity. Thus an important part of what was the physical pressure is missing in the INSE momentum equation. So we should not be surprised that the pressure in the momentum equation does not behave quite like the physical pressure. Since leading pieces (which lead via energy conservation to the continuity equation) are missing, this cannot be a thermodynamic pressure. , two orders higher than the density or velocity. Thus an important part of what was the physical pressure is missing in the INSE momentum equation. So we should not be surprised that the pressure in the momentum equation does not behave quite like the physical pressure. Since leading pieces (which lead via energy conservation to the continuity equation) are missing, this cannot be a thermodynamic pressure. So what is the interpretation of this pressure? I can say a lot about it, but I am not entirely comfortable saying what it is in physical terms. |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
Join Date: Mar 2009
Posts: 157
Rep Power: 17  |
Quote:
Interesting discussion. So where does this put compressible flows, seeing that we use the thermodynamic pressure in the cNSE, which magnitude depends on effects we do not model? Is it one part "physical reasoning" and one part numerical? |
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
Ahmed
Join Date: Mar 2009
Location: NY
Posts: 251
Rep Power: 18  |
Quote:
This is a very old discussion that dates back to the 19th centuray and when the Navier Stokes equation was written. But it would be of benfit if we recall the origin of the incompressible flow definition, so here it is, Engineers have found that in a process where changes in the density of a fluid are less than 3% can be neglected and hence we can treat the flow as a constant density fluid/flow. The result of this engineering criterion is that the divergence is Zero and hence the simplified Navier Stokes equation. In short, when that criterion is adopted, we say that density changes are neglected and nothing more than that. (bear in mind that density changes may be the result of pressure or temperature changes or both) but for engineering design purposes we neglect that change in the magnitude of the density but not in the causes of that change. Hope that will help |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Pressure instabilities with interDyMFoam for the floatingObject case | nbadano | OpenFOAM Running, Solving & CFD | 15 | October 15, 2021 06:35 |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 06:27 |
| Using pressure outlet BC | Shreyansh | FLUENT | 0 | November 5, 2010 14:57 |
| Setup/monitor points of pressure and force coefficients | siw | CFX | 3 | October 22, 2010 06:07 |
| Setting pressure and velocity in inlet | Asghari | FLUENT | 5 | September 22, 2006 13:23 |