 |
|
|
[Sponsors] | |||||
FVM for unsteady diffusion with convective BC. |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Abhi
Join Date: Dec 2014
Posts: 28
Rep Power: 11  |
I am working on a 3D cylindrical code for unsteady diffusion equation using FVM. When I am applying the Dirichlet BC and Neumann BC, I am getting grid independence however when I am applying the convective BC, the solution is changing with the refinement of grid? Can anybody explain this behavior and also how to apply the convective BC for FVM. I think I may be applying the convective BC incorrectly but then the solution should be erratic, what I am getting seems physically possible but then refinement of grid makes it spread more b/w the initial temp., To and ambient temp, Ta.
|
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,272
Rep Power: 34   |
Quote:
You mean you have convective term in purely diffusion equation? Or do you have a transport equation and it also have convective part. |
||
|
|

|
||
|
|
|
#3 |
|
New Member
Abhi
Join Date: Dec 2014
Posts: 28
Rep Power: 11  |
its a pure diffusion equation with a convective boundary condition.
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
you cannot use a convective BC.s (like d/dn = 0) in the pure diffusion problem!
|
|
|
|

|
|
|
|
|
#5 | |
|
New Member
Abhi
Join Date: Dec 2014
Posts: 28
Rep Power: 11  |
Quote:
-k( 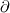 T/ T/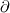 n)=h(Ts-T_ n)=h(Ts-T_ ) )
|
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
df/dn = q is a Neumann bc and can be used in the pure diffusion problem provided that q is the known physical flux. However, that is not denoted as "convective bc"
|
|
|
|

|
|
|
|
|
#7 |
|
New Member
Abhi
Join Date: Dec 2014
Posts: 28
Rep Power: 11  |
I have mentioned what I meant by convective or mixed type BC. What you wrote is a a fixed flux (i.e neumann type BC) Can u plz elaborate on the application of the mixed type (mentioned in my above comment) BC for unsteady diffusion eqn using FVM.
|
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
q is the RHS (divided by k) of your bc and must be known.
This is a non homogeneous neumann bc, not a robin one |
|
|
|

|
|
|
|
|
#9 | |
|
New Member
Abhi
Join Date: Dec 2014
Posts: 28
Rep Power: 11  |
Quote:
-k(dt/dn)=h(T  -T -T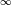 ) )
|
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Have a look at
An introduction to computational fluid dynamics. The finite volume method. H. K. VERSTEEG and W. MALALASEKERA. |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
in a 1D example, the equation is
dT/dt = d/dx(k*dT/dx) with the BC: dT/dn=-h(T  -T -T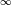 )/k =q )/k =qin a FV method, when you integrate the equation over each FV of measure h, you get dT_av/dt = (k*dT/dx|e - k*dT/dx|w)/h where |e and |w are the fluxes location at the faces of the FV. Thus, when the equation has a face coincident to the boundary, you just substitute the known flux q. Note that to produce a finite solution for any time, the Neumann BC.s must fulfill a compatibility condition otherwise dT_av/dt -> +Inf |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 06:20 |
| FVM discretization of diffusion term on crvlnr gr | Michail | Main CFD Forum | 3 | March 14, 2008 06:52 |
| FVM for diffusion problem or dispersive problems? | Wen | Main CFD Forum | 0 | February 22, 2006 13:34 |
| comments on FDM, FEM, FVM, SM, SEM, DSEM, BEM | kenn | Main CFD Forum | 2 | July 18, 2004 18:28 |