 |
|
|
[Sponsors] | |||||
Weiss & Smith Preconditioned Density Based Solver, Algebraic Multigrid, etc. |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
|
Dear all,
This is going to be a very long post. I might have splitted it in more parts, but that didn't look like the best strategy neither, after all. So, sorry about that. I'm working on the development of an unstructured, cell-centered, finite volume solver based on the preconditioned density based approach by Weiss & Smith. In particular, i'm focusing on the following work: Weiss et al., Implicit Solution of Preconditioned Navier-Stokes Equations Using Algebraic Multigrid, AIAA J. Vol. 37, N. 1, 1999 http://arc.aiaa.org/doi/abs/10.2514/2.689 which, however, obviously builds on top of their previous works in 1994, 1995 and 1997. My experience, with the code i developed up to now, is that it is actually working pretty good and, probably because of a different implementation of the entropy fix in the Roe flux difference splitting scheme (which is not mentioned in the paper; i use an all speed HLLE+ scheme as entropy fix), i might have something which is more stable and less dissipative than their method. In particular, tests on the incompressible lid driven cavity at Re 1k and 10k, on the thermally driven cavity at Ra 100k and 10M and on the 5 Toro tests on the shock tube seem to confirm this. Note that i assume the latest Fluent to be, somehow, representative of their method. I guess this assumption can't be totally inaccurate, also because people that moved from ansys to cd-adapco (e.g., Caraeni) keep referencing those works nowadays. Well, with this premise, there are still some aspects of the method (even if not necessarily related to their particular one) on which i have doubts and for which i'd really like to hear from you, experienced or not on this particular subject. Unfortunately, in this era of open source, there is no publicly available code based on this work. And even the codes by Dr. Jiri Blazek: http://booksite.elsevier.com/9780080...amplecodes.php whose book has now (3rd edition) a full description of a very similar method, do not actually implement it the way it is described. Notably, the use of conservative variables (in place of the primitive ones) and the use of a basic formulation for the preconditioning velocity make a major difference between the codes and the method described in the book. So, here we go: 1) What is, probably, one of the fundamental aspects of the method is their choice of preconditioning (matrix) and preconditioning velocity 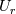 : :(1) 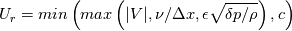 where 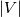 is the local velocity magnitude, is the local velocity magnitude,  is the kinematic viscosity, is the kinematic viscosity, 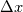 is an intercell length scale, is an intercell length scale, 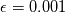 is a constant, is a constant, 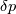 is apressure difference between adjacent cells, is apressure difference between adjacent cells, 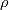 is the local density and is the local density and  is the local speed of sound (which, however, is not practically considered for fully incompressible cases as it is ideally infinite in these cases). is the local speed of sound (which, however, is not practically considered for fully incompressible cases as it is ideally infinite in these cases).Now, there is a large amount of works based on this formulation, all of them exactly reporting the same stuff. Still, there is only one relevant work which gets into the details (see page 9): http://raphael.mit.edu/darmofalpubs/JCP_vol151_p728.pdf and they thank Dr. Weiss for the suggestion on the pressure term. All the works preceding these two, to the best of my knowledge, always used a formulation similar to the following one: 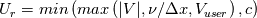 where the pressure term is replaced by an user-specified velocity. Now, i worked a lot on this and, while i used the already available pressure gradient to recover an estimate of 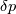 , i found that the minimum reasonable working constant that i need is , i found that the minimum reasonable working constant that i need is 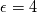 (actually i work with (actually i work with 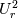 , so i actually use 20 as constant). Nonetheless, there are still cases that require a minimum , so i actually use 20 as constant). Nonetheless, there are still cases that require a minimum 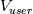 at the startup to avoid instabilities. So, the first question is: has anybody had a similar experience? Such a difference in the pressure term (3 orders of magnitude) is not something i would reduce to "depends from the specific setting". at the startup to avoid instabilities. So, the first question is: has anybody had a similar experience? Such a difference in the pressure term (3 orders of magnitude) is not something i would reduce to "depends from the specific setting".To search for an answer, i tried to reverse engineer the Fluent formulation starting from the variable that the code provides in post-processing and which, in theory, should correspond to 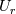 . Now, this got interesting because what i found is that (besides the specific formulation for . Now, this got interesting because what i found is that (besides the specific formulation for 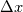 , which is quite complex and non obvious) all the terms actually correspond to the formulation used in the paper except that: a) the pressure term doesn't actually contain that small , which is quite complex and non obvious) all the terms actually correspond to the formulation used in the paper except that: a) the pressure term doesn't actually contain that small  value and b) once the value and b) once the 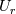 is computed according to (1), it is then multiplied by a factor is computed according to (1), it is then multiplied by a factor 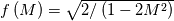 , with the resulting effect that the actual cut on the preconditioning is not for M=1 but for M=0.5. So, here it comes the second question: while this factor is also cited in the Darmofal paper above, no actual reference can be found in other works based on the Weiss & Smith one, their work included, so, what is your experience on this? Mine is that it actually slowed down my convergence a lot instead of helping it (as it was supposed to do). , with the resulting effect that the actual cut on the preconditioning is not for M=1 but for M=0.5. So, here it comes the second question: while this factor is also cited in the Darmofal paper above, no actual reference can be found in other works based on the Weiss & Smith one, their work included, so, what is your experience on this? Mine is that it actually slowed down my convergence a lot instead of helping it (as it was supposed to do).2) My second doubt is about how the second order is implemented within the Roe flux difference splitting scheme when working in primitive variables (u,v,w,p,T). While in the Weiss paper they explicitly state that they do not use Roe but simple averages, i decided to follow a more regular route and use the Roe ones. However, while the implementation is quite obvious when working in conserved variables (see Blazek codes), it is not anymore in primitive ones (at least not for me). Indeed, to compute Roe averages one needs the left and right density states but two options are possible: a) compute cell centered density gradients and extrapolate them as the remaining primitive variables; b) use the extrapolated p and T to build, trough the thermodynamic relations, the density. So, the question is: while i use option (a), i feel (b) might be the consistent one (also because that's how cell centered density values are obtained in the first place). What do you think about it? The same also applies for the enthalpy, of course (which is the other dependent variable). A similar aspect regards instead the preconditioning velocity, which is needed on the cell faces for the convective scheme and in the cell centers for the pseudo-time derivative term. I decided to compute and store it in the cell centers, using a Roe average for its value on the cell faces. How do you compute it? I also tought about not storing it at all and computing it consistently wherever required, but i'm not yet sure about the performance issues this would imply. 3) The third aspect which puzzles me is the overall advancement in pseudo-time toward a steady state. The original paper does not mention at all the possibility of using under-relaxation factors (URF). So the idea should be: "use the largest stable CFL with unitary URF". However, the chance of using them is clearly there and, indeed, i typically found that a minimum is really necessary, at least at startup. What are your experiences on this? Sometimes i found the Fluent strategy faster than using URF, but i couldn't find a definite answer on this. Note, however, that Fluent has a separate "pseudo-time something" option (which actually sets the local time step instead of the global CFL), without which i typically found Fluent to diverge, no matter how simple the case is or how small the CFL is set. 4) At the moment, my code relies on PETSc 3.7.2 for the linear algebra part. That is, at each pseudo-time step the linearized system is soved by a SGS preconditoned GMRES. As an alternative i also have an internally coded block SGS solver. While, for the moment, i am pretty happy with them, i would like to move to AMG in the future. However, so far, my experience on this has been quite disappointing. After a long struggle i managed to work with hypre BoomerAMG (still trough PETSc as GMRES+AMG) but: a) whenever AMG worked as expected (e.g., lid driven cavity), it was no more performant than SGS as preconditioner, in terms of non-linear outer iterations required to converge to a specified tolerance (in practice, solving the linear problem to machine accuracy in few iterations, which is the advantage of AMG, did not improve the outer iterations convergence); b) in some cases (e.g., thermally driven cavity) it completely failed at the first inner iteration while SGS preconditioning still worked like a charm (in this specific case the implicit part due to gravity worked against the stability for AMG, while increased it for SGS); c) in no case i was able to use Hypre BoomerAMG as solver (opposed to preconditioner) as proposed in the Weiss et al. paper. Now, i am working toward using the PETSc native AMG (instead of the hypre one) as well as on using Hypre directly (and not trough PETSc) but, i was wondering if someone of you has some experience in using their AMG (hypre or PETSc) in cell centered finite volume codes and would like to share it. I know that the workhorse in commercial CFD codes, as also reported by the Weiss paper, is the additive correction strategy by Hutchinson and Raithby (obviously adapted to the non structured case). What i don't know is if this method is somehow replicable with the tools available in PETSc or Hypre. Probably PETSc AMG with NON smoothed aggregation should be close to that, and that's the route i'm following right now, but i'm not really sure. I know that i should have asked on the PETSc mailing list first but, i saw people asking for the exact same thing and eventually ending up implementing their own AMG because of the total non-sense of the answer they got. In principle i could also try implementing it by myself, but the parallel aspects are those that scare me off the most (besides the fact that it might easily be one of the things which do not work as described in the reference paper). Working on a serial version (or AMG over each subdomain) does not seem, at the moment, a strategy which would pay off (considering that i already have the linear algebra working). So, i ask: is there some obvious way to implement the Additive Correction Algebraic Multigrid in parallel which i'm not seeing? I know that most of these questions are more easily answered hands-on trough testing but, i already found, somehow, a sweet spot for my overall setting (in math terms, the local minimum/maximum) and i found it difficult to move from here one aspect at the time. So i tried to separate the aspects i have doubts on (the ones above) from the others, before moving on. Hopefully, with your help, i can get this straight. Moreover, consider that i have no strong background on any of these topics; so, even stupid, probably obvious, hints are welcome here. Thank you all for your attention. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Paolo, I am not able to give a real help about these issue but I can just say that the primitive variables approach cannot be suitable for working with flux-based method.....or at least I am not aware of that
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
I have spend most of my time working on pressure-based algorithms. I have read many of the papers you reference, but I have not implemented any of those schemes myself.
I can offer some recommendations about AMG. Parallel AMG generally does NOT coarsen across parallel domain boundaries. This is a part of the reason why AMG convergence characteristic are different for different parallel partitionings/CPU counts. Where I implementing these algorithms now, I would do two things: (1) implement mixed OpenMP/pthreads with MPI to better handle 16+ core shared memory segments and allow coarsening on all meshes on the same shared-memory node. (2) look at additive Schwartz approaches that introduce additional layers of ghost cells for parallel decompositions and permits more locality in the smoother portitions and more consistent convergence. Also, while you didn't ask, I would also mention that if you are rolling your own grid agglomeration algorithms, you might consider doing it for the full non-linear problem and building an FAS solver. You will need hierarchical grids with connectivity, face areas and centroids, and cell volumes and centroids, but whatever your current solver currently does could be used as a smoother such an FAS formulation. You might find better overall performance with this approach versus, even if it just an FMG start-up method to prime the fine-grid solution. I sincerely wish I had more insight into your other questions. They are all tempting topics, but I can't spare the time to dig too deeply into them now. Good luck. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
While I can't help you with your quest for the reason that i never implemented density based solver, however i do have this paper and had a look.
You should remember two things (which actually you get but i enforce it). 1. Fluent and Starccm at the base are this method. As you mentioned people moving from fluent to adapco. 2. Both these solvers at their base are written long ago. Fluent before 1999 and starccm started off in 2001 so expect that it was first written around 2002 or so. But then lots of people have made changes in the code because of feedback from users on various aspect and then people other than Wayne and Jonathan working on them. So expect that in last 10 to 15 years a lot to be changed and the changes are due to other people. |
|
|
|

|
|
|
|
|
#5 | ||
|
Senior Member
|
Quote:
i guess that it probably went unnoticed, due to the long post, but i actually have a working code. However, if you delve into the details of the formulation, you will see that, to formulate the flux, the primitive variables (their differences entering the "upwind" part of the formulation) are first properly transformed. When advancing in time explicitly (or solving the linear system implicitly) then everything is transformed back to the primitive formulation. In practice, the overall approach is not really different from an artificial compressibility method, just solved coupled instead of segragated, and with a specific convective scheme. Moreover, primitive variables are strictly necessary when solving in the incompressible limit, where density will stay constant. Still, i really cannot avoid thinking that no examples of such an approach are available, and you might be right in that, in practice, this is not how it is implemented. But, again, i have a working code, and i'm not considering to change the primitive variable approach until, somehow, forced to do it. Which, in practice, is the reason i started this post, trying to have all the pieces of the map right, to correctly draw the path to my final destination. Quote:
that really is a valuable piece of advice which, i guess, would somehow explain also why some teams have put a certain effort in dropping the AMG part to the local accelerators. However, what i have doubts on is the following. Let us assume that every processor has its own coarsening limited to its own sub-domain. This, i guess, means that no ghost cell is ever agglomerated to any of the local coarse cells. Up to this, i still follow. What i miss is: how do you locally handle the agglomeration among ghost cells which is taking place in a different processor? Is this something to consider? I guess that this strictly depends from when, in the process, ghost cells are exchanged. If these are only exchanged at the beginning of each cycle, then i could also consider something like: - do the ghost exchange - move ghost terms to the RHS - do local AMG cycle (a purely serial version) - collect residuals and repeat Did you refer to something like this? Or maybe you suggest to have, with sufficient layers of ghosts, a local agglomeration of ghost cells (where feasible, of coarse)? Otherwise, having to handle all the off-processor agglomerations and relative exchnages really looks like a sort of parallel AMG implementation to a novice like me. Probably, the whole point here is that i'm really thinking the AMG on top of the matrix structure instead of the grid one (which somehow you seem to suggest). I know that the additive correction flavour is not a "black-box" AMG solver but, somehow, i liked the idea to write something expendable on a general matrix. Thanks |
|||
|
|

|
|||
|
|
|
#6 | |
|
Senior Member
|
Quote:
that's also a point. Also, for very obvious reasons, i can imagine several details to be missing from their papers. Still, i find hilarious that works made after those simply refer to the exact same approach. |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Paolo I cannot help, I don't know the details of this formulation...I wonder what numerical flux function is formulated ....
I mean, starting from the system of equations written in conservative form you can derive the quasi-linear form by expliciting the Jacobian but the primitive formulation has a very different structure of the matrix... I would learn how the numerical fluxes are formulated starting from the quasi-linear form of the primitive formulation.... 
|
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
Quote:
Second, you coarsen locally first before you do anything with ghost cells. Once you have all of your mesh levels built, then you assemble the ghosts cells FOR EACH level of the mesh. Then when you communicate across the parallel boundaries, you send ghost data for all of the mesh levels. Note that you will end up with some odd-shaped cells and odd numbers of neighbors and because you don't coarsen across parallel boundaries, you may have multiple ghost cells touching an internal cell where you'd only expect one. You may be able to avoid this by agglomerating parallel interface FACES first, communicating that agglomeration to both PEs and then coarsening the cells to match. Honestly, I don't think that is commonly done...the coarse meshes are going to have awkward shaped cells with poor interpolation accuracy even away from the parallel interfaces. It is generally sufficient for them to just be representative of the bulk solution behavior to provide convergence benefits. Third, i'd recommend that you read up on Additive Schwarz before you go too far down the pure MG development path. SGS-smoothed MG is still a valid solution scheme/preconditioner but is honestly a poor fit for current and future massive core SMP systems. Additive Schwarz allows large amounts of work to be done (in cache) on blocks of the problem as a preconditioner and then stitched together via GMRES and/or Newton-Krylov. It gives you more tuning flexibility, and you can always dial it down to one ghost layer and one additive block per PE and get right back to where a normal MG scheme would be. David Keyes papers cover these techniques in some detail in a NK context. That is where I came to learn about them. Again, I wish I had more to offer. |
||
|
|

|
||
|
|
|
#9 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
The commercial codes don't agglomorate across the processors. My code (FVUS/wildkatze) too does not coarsen across the processors.
I do have interest in implementing generalized R.A.P (or coarse operator) which shall support coarsening across processors. But I am short on time and I also think that the impact is not worth exploring as most of the problem could be handled by better smoother. I have polynomial smoother implemented in Wildkatze for exactly same purpose. This one http://www.sciencedirect.com/science...21999103001943 I did implement this for starccm too (which did not make to release version) and I tried it with coupled solver (that you have) and I could see that it worked better than other smoothers. So I think if you are facing problems in parallel part first explore this option, if problem still persists try coarsening across partitions (for additive corrective AMG it shall be relatively easier, for other AMGs it could be real pain in A). |
|
|
|

|
|
|
|
|
#10 | |||
|
Senior Member
|
Quote:
this was also one of the concerns i had (the ugly part you described, reported below). What i don't get is how this is going to work for systems which are the result of a linearization (while it is crystal clear why it is the method of choice for, say, the pressure equation). At a given iteration i might have a matrix with different entries in different positions with respect to the previous iteration. Now, one of the few things i think i got about AMG is that the burden on the smoother which is typical of geometrical multigrid (line, zebra, alternating planes, etc.) is moved to the agglomeration strategy, which works according to the matrix structure and entries. If my agglomeration is frozen, i don't see anymore how this is going to work. Even considering that Weiss et al. only used the A(1,1) coefficient of the 5x5 matrix block A (similarly to what Raw et al. did for the coupled pressure solver in CFX), that still contains a non-linearity for an all-speed solver (i.e., the matrix coefficient depends on the solution). Quote:
 . .Still, i guess i can surely find some hints in PETSc/Hypre on how to do it starting from the matrix, instead of the mesh. Quote:
thank you for the suggestion. While i'm not considering any other smoother at the moment, i understand that the whole story that the agglomeration takes care of everything in AMG is certainly not always accurate. Still, i would not probably go beyond ILU(0) as linear algebra is not exactly my field and i could end up spending months in something wrong without realizing that. |
||||
|
|

|
||||
|
|
|
#11 | |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
Quote:
The AMG concept is that the A matrix leads directly to the hierarchical coarse matrices and guides the inter-grid transfer operations and it is driven by the desire to produce a drop-in replacement for ICCG or ILU-GMRES that will work with any sparse matrix. FVM/FEM derived matrices a certainly not general matrices. If you build the mesh hierarchy and reuse it, say as a list of cells that are agglomerated to form each coarse cell, then you have a template to take a new A matrix, press it down through the coarsening template that you have already assembled and fill hierarchical data regions that are already pre-allocated and populated with connectivity information. Then, coarsening A becomes a fully local process and you already know what ghost information has to go to which PEs. A_fine -> A-course, x_fine -> x_coarse, b_fine -> b_coarse all by the recipe. You may find that some mesh coarsenings don't work well for all transport equations due to aspect ratios, flux/flow directions, or extreme differences in, say, diffusivities. If that is the case, you can coarsen and store a different recipe for each special case transport equation, as needed. But again, you do that once or occasionally and most of the time reuse the same recipe. And yes, I don't want to over-simplify the process. You are right to be wary of it. But, if you do build it, then you have a powerful tool both for linear and non-linear preconditioning and smoothing. But before you do any of that, again, I recommend that you look at Schwarz decompositions. You may find that heirarchial meshes are not necessarily, but just doing a few (fully local) iterations of GMRES leads to better rates of convergence and solution stability. |
||
|
|

|
||
|
|
|
#12 | |
|
Senior Member
|
Quote:
Just out of curiosity, i checked what Fluent does with the density based algorithm (lid driven cavity at Re 10k), and it seems that, at least for the first 20 iterations, it keeps changing the number of cells in the multigrid levels (in both serial and parallel, with the default F-cycle for my case as well as with a V-cycle). However, once the whole method is in place, i guess that using it once or at every iteration is just a matter of choice (and good programming). I am not ignoring your advice on (DD) Schwarz methods. Actually, i am pretty sure that they are, in some flavor, already available in PETSc (PCASM, or something like that) and i would have given them a straight try... but, today, the site of MCS division @ ANL seems completely off and i cannot find any copy of the manual at the moment. I'll let you know how that goes vs. a full GMRES+SGS. |
||
|
|

|
||
|
|
|
#13 | |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
Quote:
|
||
|
|

|
||
|
|
|
#14 | |||
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
Quote:
Quote:
Since polynomial smoothers work only on matrix vector product that are not affected by partitioning. But if you have ILU(0) implemented than it works good for coupled system. |
||||
|
|

|
||||
|
|
|
#15 | ||
|
Senior Member
|
Quote:
that's interesting as i know for sure that (for steady state cases) i only have the time step at the denominator of a matrix with only positive terms on the diagonal (the preconditioning matrix 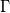 in the paper). In contrast, i only have possibly negative terms in the convective part (central flux jacobian and upwind correction, but i'm not sure on their combined behavior), without any time step involved. Am i missing something? What i tipically observe is that: in the paper). In contrast, i only have possibly negative terms in the convective part (central flux jacobian and upwind correction, but i'm not sure on their combined behavior), without any time step involved. Am i missing something? What i tipically observe is that:1) For a given problematic case i can lower the CFL until i get stability (if things are problematic it means i'm also already using URF). 2) If (1) is not working i tipically need to increase the 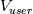 from the default 0 value to few % of the characteristic velocity in the domain. from the default 0 value to few % of the characteristic velocity in the domain.Quote:
 . What i meant is that, besides Fluent, there are dozens of papers using GMRES+ILU on the preconditioned density based solver. So, i would not have to invent anything and just use a proven recipe. In contrast, i have no clue on the feasibility of other options (e.g., why, in the paper you cited, they just focus on symmetric matrices if the method is also applicable to non-symmetric ones?). . What i meant is that, besides Fluent, there are dozens of papers using GMRES+ILU on the preconditioned density based solver. So, i would not have to invent anything and just use a proven recipe. In contrast, i have no clue on the feasibility of other options (e.g., why, in the paper you cited, they just focus on symmetric matrices if the method is also applicable to non-symmetric ones?).
|
|||
|
|

|
|||
|
|
|
#16 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
Quote:
PS: From the person who as looked into this AMG stuff or have implemented most of these things, keep in mind that polynomial smoother will be easier to implement than ILU type. (it is whole lot of discussion about why so lets leave it for now). |
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
What polynomial did you use? Chebychev? How did you do your spectral radius estimates? That always seems like the complex point to me. The rest is just matvecs.
|
|
|
|

|
|
|
|
|
#18 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
Currently its Arnoldi iteration based in Wildkatze solver. I can share the implementation in case someone implements it. Here is the working code from FVUS/Wildkatze. (works for block matrix too, as you can see from bsize) Code:
void
Smoother::
spectralRadiusArnoldi()
{
int const blkSize = _A->blockSize ();
int const bSize = _A->rows () * blkSize;
int const tsize = xSize ();
int const maxiter = _maxSpRadItrs;
int const currLevel = _A->getLevelIndex();
if (bSize < 1)
return;
delete[] _di;
_di = new double[tsize * blkSize + 4];
std::vector< std::vector<double> > Vvec;
Vvec .resize(maxiter + 1);
std::vector<double> oneBySqrtDi;
std::vector<bool > isActive;
std::vector<double> vvec;
std::vector<double> gvec;
std::vector<double> hvecLong;
std::vector<double> Hvec;
oneBySqrtDi.resize(bSize);
isActive. resize(bSize);
vvec. resize(bSize);
gvec. resize(bSize);
hvecLong. resize(tsize);
Hvec. resize((maxiter + 1) * (maxiter + 1));
double const small = 1.0E-20;
// 1 / sqrt( Dia )
// isActive will find the Dirilichet bc and degenerate points
getOneBySqrtDia(oneBySqrtDi, isActive);
/// it works with col = 0, 1, 2, .....
int currCol = 0;
for (int i = 0; i < Hvec.size(); i++)
{
Hvec[i] = 0;
}
for (int i = 0; i <= maxiter; i++)
{
Vvec[i].resize(bSize);
}
double sum_sqr(0);
srand(time(NULL));
for (int i = 0; i < bSize; i++)
{
if (isActive[i])
{
Vvec[currCol][i] = (double) (std::rand() / ((double) RAND_MAX));
sum_sqr = sum_sqr + Vvec[currCol][i] * Vvec[currCol][i];
}
else
Vvec[currCol][i] = 0;
}
sum_sqr = GlobalMpiCommGroup::getSingleton().allSumD(sum_sqr);
// the l2 norm
// note: using the inverse
sum_sqr = 1.0 / std::sqrt(sum_sqr);
/// normalize it
for (int i = 0; i < bSize; i++)
{
Vvec[currCol][i] = (isActive[i]) ? (Vvec[currCol][i] * sum_sqr) : 0;
}
for (int curr_itr = 0; curr_itr < maxiter; curr_itr++)
{
for (int i = 0; i < bSize; i++)
{
vvec[i] = (isActive[i]) ? Vvec[currCol][i] * oneBySqrtDi[i] : 0;
}
_A->matrixVecProduct(vvec, gvec, hvecLong);
for (int i = 0; i < bSize; i++)
{
gvec[i] = (isActive[i]) ? gvec[i] * oneBySqrtDi[i] : 0;
}
//// Orthogonalize against Vs
for (int index = 0; index <= currCol; index++)
{
// for v = V[index]
Hvec[index * (maxiter + 1) + curr_itr] = vecDotProduct(Vvec[index], gvec);
for (int i = 0; i < bSize; i++)
{
if (isActive[i])
gvec[i] = (gvec[i] - Hvec[index * (maxiter + 1) + curr_itr] * Vvec[index][i]);
}
}
Hvec[(curr_itr + 1) * (maxiter + 1) + curr_itr] = std::sqrt(vecDotProduct(gvec, gvec)); // norm(w); // norm2
// if (Hvec[curr_itr +1,curr_itr ] < breakdown):
for (int i = 0; i < bSize; i++)
{
gvec [i] = (isActive[i]) ?
(gvec[i] / (Hvec[(curr_itr + 1) * (maxiter + 1) + curr_itr] + small))
: 0;
Vvec[currCol + 1][i] = gvec[i];
}
currCol++;
}
// next is power iteration to estimate max eigenvalue
double sum, lambda = 0, para;
unsigned int iter = 30;
double tol = 1E-5;
std::vector<double> x;
x.resize (maxiter + 2);
std::vector<double> x0;
x0.resize (maxiter + 2);
for (unsigned int i = 0; i <= maxiter; i++)
{
x0[i] = 1;
}
for (unsigned int i = 0; i < iter; i++)
{
para = lambda;
for (unsigned int j = 0; j < maxiter; j++)
{
sum = 0;
for (unsigned int k = 0; k < maxiter; k++)
{
sum = sum + Hvec[j * (maxiter + 1) + k] * x0[k];
}
x[j] = std::fabs(sum);
}
lambda = x[maxiter - 1]; // stores the highest eigen value
for (unsigned int l = 0; l < maxiter; l++)
{
x[l] = x[l] / (lambda + small);
}
if (fabs(lambda - para) < tol)
{
break;
}
for (unsigned int l = 0; l < maxiter; l++)
{
x0[l] = x[l];
}
}
// delete the memory
for (unsigned int i = 0; i <= maxiter; i++)
{
Vvec[i].resize(0);
}
Vvec.resize(0);
// Does not allow negative value. Negative value typically arise
// from failure of spectral radius calculations.
// Again it does not have that frequently but when it happens
// it might make simulation diverge. This is safegaurd against such failures
lambda = std::fabs(lambda);
setSpectralRadValue(lambda);
MultiLevLinearSolver* mlSolver = _A->getSolver();
double mSpRa = lambda;
if(mlSolver)
mSpRa = _A->getSolver()->getMaxSpectralRadius();
setSpectralRadValue(mSpRa);
}
|
||
|
|

|
||
|
|
|
#19 |
|
New Member
Karpenko Anton
Join Date: Aug 2009
Location: Saint-Petersburg
Posts: 4
Rep Power: 16  |
Sorry for my English))
Paolo, 1) In my program codes I did not use the pressure gradient 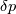 for preconditioning velocity. for preconditioning velocity. But calculations were carried out on similar relations (for example, for a compressible gas): 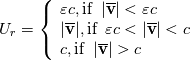  -- is small parameter, if V very small -- -- is small parameter, if V very small -- 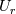 not tends to zero and remains constant. not tends to zero and remains constant.When calculating the viscous flux is necessary that the velocity of propagation pseudo-acoustic perturbations 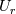 is not less than the velocity propagation of viscous perturbation: is not less than the velocity propagation of viscous perturbation: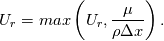 Some refs about problem: Fist work for pseudo compressible flows -- Chorin A.J. A numerical method for solving incompressible viscous flow problems // Journal of Computational Physics. 1967. Vol. 2. No. 1. P. 12--26. D. Choi, C. L. Merkle Application of time-iterative schemes to incompressible flow // AIAA Journal, 1985, Vol. 23, No. 10, pp. 1518-1524. Y.H. Choi, C.L. Merkle The Application of Preconditioning in ViscousFlows // Journal of Computational Physics, 1993,Vol. 105, Issue 2, P. 207–223 E. Turkel Preconditioned Methods for Solving the Incompressi and Low Speed Compressible Equations // Journal of Computational Physics, 1987, Vol. 72, p. 277-298 2) In Weiss paper and my code I do not use Roe averges, but use simple averages. Roe flux difference splitting scheme looks: 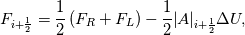 U -- is conservative variable, dissipative term transforms: 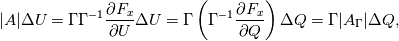 Where Jacobian precondition system is: 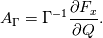 Then diagonalize Jacobian we get: 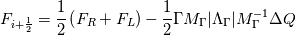 For solve 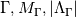 use simple averages. use simple averages.3,4) I do not know about this, because i use only explicit schemes. |
|
|
|

|
|
|
|
|
#20 | |
|
Senior Member
|
Dear Anton,
first of all, thank you for your help. Quote:
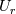 just because it had another small parameter ( just because it had another small parameter (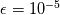 ) which was, again, much smaller than what i typically need (order 1 without pressure gradient, order 0.1 in problematic cases when i use the pressure gradient term). What is your experience on this? I also tried to use the Fluent recipe for ) which was, again, much smaller than what i typically need (order 1 without pressure gradient, order 0.1 in problematic cases when i use the pressure gradient term). What is your experience on this? I also tried to use the Fluent recipe for 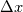 but, again, it turned out to slow down my convergence a lot for incompressible cases. Now i simply use the smallest cell dimension. but, again, it turned out to slow down my convergence a lot for incompressible cases. Now i simply use the smallest cell dimension.Quote:
 ). Is there any particular reason for which you decided to use averages (instead of Roe averages), besides trying to follow closely the paper? ). Is there any particular reason for which you decided to use averages (instead of Roe averages), besides trying to follow closely the paper?So, i guess, you also use simple averages for 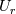 on the faces when computing the fluxes. on the faces when computing the fluxes.
|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Pressure based and Density based Solver | Xobile | Main CFD Forum | 39 | August 19, 2020 06:04 |
| "Solid" in density based solver | songpen1985 | Fluent Multiphase | 0 | July 2, 2015 04:52 |
| algebraic multigrid vs geometric multigrid | Anna Tian | Main CFD Forum | 5 | June 18, 2013 05:03 |
| Strange residuals of the Density Based Solver | Pat84 | FLUENT | 0 | October 22, 2012 15:59 |
| MIGAL- coupled algebraic multigrid solver? | George Bergantz | Main CFD Forum | 0 | December 1, 2000 01:39 |