 |
|
|
[Sponsors] | |||||
Another discussion on velocity-pressure coupling |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Dec 2015
Posts: 27
Rep Power: 10  |
Hi all,
I am looking to get some different, more rigorous insights on the infamous velocity-pressure coupling in incompressible flows. First off, I always come back to this thread, which I really enjoy; however, I need to hear more peoples take on this topic. I understand that pressure works as a Lagrange multiplier to enforce the incompressibility constraint, and I have gone through several exercises using Stokes' equations to prove this. Whenever I think about this, I always look at in matrix form. The saddle-point problem is 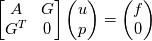 So in terms of the Lagrange multiplier, I view pressure as additional "arbitrary" unknowns that fill the columns of the system matrix so that there are an equal number of equations and unknowns. Without such pressures, assuming that the trial space is the space of all H^1, there would be more equations than unknowns and thus overdetermined. If instead, the trial space is all divergence-free H^1 functions, then there is no need for the constraint equation and thus no need for the pressures. So from a physical perspective, can we think of this as a weird type of one way coupling? The velocity affects the pressure, but the pressure does not really affect the velocity in the normal way we are used to thinking. I know this technically isn't correct since the whole point of pressure is to force the velocity to be solenoidal; however, the pressure can be whatever it needs to be to do this. For example, I was playing around with this on a FEM Stokes' solver I wrote. I was curious what would happen if I changed the discretization of pressure to something completely wrong. What happened was interesting. The velocity didn't change, only the pressure did. So all though this erroneous pressure does keep the velocity solenoidal, it seems it is completely arbitrary; just a mathematical artifice. I guess I am just having trouble reconciling the math and physics here. Maybe its not even possible with incompressible flows? I would very much appreciate all of your insight on this weird phenomenon. |
|
|
|

|
|
|
|
|
#2 | ||
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
Quote:
Quote:
I know the discussion is for incompressible flows, but you're starting with the assumption that pressure somehow magically makes (all) flows divergence free. You are assigning properties to the pressure field that it doesn't normally have, it only has that behavior after you assume the velocity field is divergence free. |
|||
|
|

|
|||
|
|
|
#3 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
I am not sure about the actual key of the question, I have my opinion about the general issue:
1) first, we call pressure only a mathematical function that acts by means of a gradient. That has no physical meaning related to the classical action of the pressure. 2) if I multiply the momentum equation for the velocity vector field and integrate, the "pressure" disappears. In this sense, the pressure has no action on the velocity field. However, this is the classical weak form for which a possible solution is not necessarily unique. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
|
Not really an expert here, especially not in math related stuff. Still, let me give you my 2 cents.
When you take the divergence of the incompressible momentum equations, you end up with a poisson equation for the pressure which, formally, has a solution trough the biot-savart law. It's an integral involving only the velocity field. You can put that back in the momentum equation and you end up with a single equation for the velocity field (ok, 3, but you know what I mean). Which is along the line of what you mentioned. The integral nature of the equation means that the velocity in each point of the domain is affected by the velocity in any other point in the domain. No more pressure involved. Now, question: by looking at such equation, do you understand the physical behavior of fluids under incompressible flow conditions? Also, do you interpret the relative PDEs according to their physical meaning (I mean, you have a physical system that happens to closely follow your PDE, you should at least consider it in order to understand your PDE)? The real point of the matter here, I think, is if you are interested in this questions or not. If you are, I don't think you can neglect where the equations really come from and how you reach that limiting behavior known as incompressible flows, which actually doesn't physically exists, it's just how things seem to happen under an uncorrect time scale. So, as others have stated, you might look at the pressure as auxiliary variable, but you can also look at pressure as that very variable that balances momentum equation with its gradient while actually being subject to a poisson equation. There's actually only one such field for well posed conditions... + an arbitrary constant for incompressible flows. But do we actually observe that constant to be really arbitrary? Only in the sense that we can have an incompressible behavior around most baseline pressure values. Such baseline value does not seem to play a role in the flow dynamics as long as it stays incompressible. Still, not all baseline pressure values are physically possible for an incompressible behavior. Put still differently: if you decided the pressure role should be simplified to the incompressible case, does this change its role in the matter? I don't think so. My point of view is that the pressure role for incompressible flows is just exactly the same for compressible flows. It's just us that, looking at the flow behavior under an uncorrect time scale (so that we filter out the compressibility), only see this lagrange multiplier that automagically makes the velocity field divergence free. That correction to the velocity field actually happened in a finite time, constrained by an hyperbolic equation for the mass. So, in conclusion: yes, you can get the velocity field without knowing the pressure (it actually happens for streamfunction-vorticity approaches) and consider the pressure as whatever mathematical object best fits its role in your simplified incompressible equations. Is this view correct? I don't think so (or only partially). To me it is just a mathematically obfuscated interpretation of a physical field which happen to have a very specific role in the dynamics of the equations it appears in. That dynamics is just the same as for compressible flows, just much faster than the flow velocity. In a more broad sense, is like if the time filtering responsible for the incompressible approximation has made the problem non unique with respect to the variable involved (i.e., you can't recover the unfiltered variable from a filtered one if filtering leads to a loss of information). From the math point of view you are free to search for any possible solution to your problem. Physically, I knew what the true unfiltered solution really was and I'm not interested in the other ones (nor, I think, are those who need computations to analyse physical scenarios). P.S. +1 for the thread title |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Let me just recall that if the model is based on the assumptions rho and temperature constant, we have mathematically grad p=0. Therefore, it is clear the mathematical artifact of introducing such a gradient...
|
|
|
|

|
|
|
|
|
#6 | |||||
|
New Member
Join Date: Dec 2015
Posts: 27
Rep Power: 10  |
Quote:
Quote:
Quote:
Quote:
Quote:
|
||||||
|
|

|
||||||
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Just to highlight some points:
1) why the velocity for incompressible flows should not be onto the subspace of divergence-free functions? 2) the continuity equation remains hyperbolic also in the incompressible model. It is transformed in an elliptic equation for the pressure. Again, this is a consequence of the model. 3) Physically, the pressure has always action on a flow motion but here we are discussing about a mathematical model where rho=const, T= const therefore p=constant if we would use the thermodynamics. Formally, no pressure gradient would appear in the momentum and we have one equation for one unknown constrained by the divergence-free equation. 4) considering the low-Mach model, maybe it would be more physical from your point of view. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Forget to say to have also a look to the brief paragraph in the book of Peric & Ferziger
|
|
|
|

|
|
|
|
|
#9 | |
|
Senior Member
|
Quote:
https://crd.lbl.gov/assets/pubs_presos/AMCS/ANAG/A213.pdf https://link.springer.com/article/10.1007/s002200050308 In the first link you will also find the commonly used form of the equations for the low Mach limit. From that you see that you really need to look at the incompressible limit as an expansion around a background thermodynamic pressure, so nothing really collapses there (not even the physical meaning). Another way I like to see the matter is by deriving a pressure equation from the density one (obtained itself by taking the divergence of the momentum equations, the time derivative of the continuity equation and mixing the two): ![\frac{\partial^2 \rho}{\partial t^2} =
\frac{\partial^2}{\partial x_i x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] \frac{\partial^2 \rho}{\partial t^2} =
\frac{\partial^2}{\partial x_i x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right]](/Forums/vbLatex/img/5fa795eb9d663dd3950c0b7a5ce1f803-1.gif) where 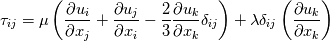 If you expand the density in terms of the pressure and temperature you end up with a wave-like equation for the pressure. If you look at that as a sort of spring-mass system where the role of the spring constant is played by the sound speed squared, you really see the physics going on here. The faster the sound the faster the system gets to the equilibrium. Infinitely fast for me then just means instantaneous equilibrium. The filtering analogy comes from considering any steady state equation as coming from a time average over an infinite time interval (e.g., RANS equations are obtained in this manner). I agree on the different nature of the equations when the temporal term exactly disappears, but from the physics point of view you can agree, I think, that filtering better represents what is really going on while producing the exact same result (the unsteady term disappears). So, if your point is understanding what's the role of the pressure in the incompressible limit, I think you can still look at it only from the math point of view. What I'm saying is just that if you want to understand why it looks so weird you have to understand what's going on physically. Now you tell me how all of this can be translated in the algebraic view you started with  (*) EDIT: I clearly misunderstood your use of the term singularity, which is correct and I actually agree upon it. Still, what I meant in practice (that there is convergence in the limit) still applies. Last edited by sbaffini; August 9, 2017 at 09:42. |
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Maybe, a simple physical example can also seen in the 1D Euler equations. The eigenvalues u-a,u,u+a and the slopes of the characteristic lines 1/(u-a),1/u,1/(u+a) could give a simple picture of the physical meaning of the pressure waves for Ma->0. Of course, that not exactly correspond to the assumption rho=const and T=const but gives some ideas.
|
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
|
As this never comes out in such discussions, I just want to add another point of view.
When a Fourier representation of the velocity field can be applied, the pressure also seems to disappear from the incompressible picture. That is, you can solve for the velocity without considering the pressure by applying a projector to the non linear terms. What is hidden from the view is that the pressure is still there, balancing the remaining part of the non linear term. So, in a certain sense, the role of the pressure for incompressible flows is to always balance a certain part of the momentum equations. If you can write those two part autonomously with a proper projection then you are obviously free to treat them separately. But would you conclude that pressure is ininfluent or that you were clever enough to separate the two parts of the problem? Perhaps (but this is matter for Filippo), this is just the very heart of the Helmholtz-Hodge decomposition. The incompressible pressure is there just to balance the gradient part of the velocity field (so that it never produces a divergence). But, as such, it is only a correction over a baseline thermodynamic pressure which, in contrast, doesn't affect the incompressible momentum equations. |
|
|
|

|
|
|
|
|
#12 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
When I analysed this issue, my first thought was to write the momentum equation as it is (without introducing any fractional method for the time integration), in terms of the acceleration a +grad p = a*. And this is nothing else that still a form for the Hodge decomposition. What we call "pressure", is just a potential function for an acceleration a' that must ensure the divergence-free constraint for the field a= a*-a'. There is no thermodynamic pressure in this issue. Thermodynamic pressure should be just p=rho*R*T = constant and the pressure gradient is zero. Since the decomposition is valid even for inviscid flows (a* has only the convective term) and we know that Bernoulli (unsteady) integral exists, we can try to think about a dynamic pressure equivalence. |
||
|
|

|
||
|
|
|
#13 | |
|
Senior Member
|
Quote:
Also, note that preconditioned density based codes written for primitive variables (p,u,v,w,T) can always compute a pressure and its gradient, even for fully incompressible flows. It is the density that then shows up as constant (but in such codes that's just a dependent variable). In this case, the only way for the pressure to sense its background thermodynamic part is via boundary conditions. If you look at the expansions of p in terms of M, to the lowest order, the thermodynamic part of the pressure is constant, and the acoustic one is constant to a certain extent. So, the gradient part, to the lowest order, is really the dynamic one only. |
||
|
|

|
||
|
|
|
#14 | ||
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
Quote:
You are considering coupling as between distinct objects (a separate fluid and a separate structure). In fluid-structure coupling they each can have their motions that can be completely uncoupled from the other, we call certain special interactions where they affect each other coupling. In pressure-velocity coupling, they always affect each other and are always coupled, which makes it difficult to say who is affecting who because you cannot pull these effects apart. It's not that the coupling is one-way and only goes from velocity to pressure. The coupling in this case is just so strong they are less independent from one another. Using the pressure driven pipe flow as both a compressible and incompressible example... You are saying that for a given flow or velocity field, the pressure gradient is unique and therefore velocity affects the pressure but not the other way around. A numerical example is you applied the mass-flow rate as a boundary condition and you measure the resulting pressure gradient. Thus the pressure reacts to the flow and not the other way around. What you did not consider is the case where you apply the pressure difference as your boundary conditions and then observe or measure the velocity field. So for a given pressure gradient, what does the flow in the pipe look like? Physically you do this more often. To achieve a flow in a pipe you generate a pressure head by using a pump or an elevated (water) tank elsewhere. I.e. you started with a known velocity field without questioning how it got there. Note that when we say that for an incompressible flow the pressure is whatever it needs to be to satisfy the divergence free constraint, we have assumed that the velocity field already is divergence free. The caveat is that when we solve these things we tend to impose the velocity constraint first so that it is already satisfied which gives the appearance that only pressure changes and not velocity. Velocity has already changed without us noticing. Quote:
Last edited by LuckyTran; August 10, 2017 at 16:29. |
|||
|
|

|
|||
|
|
|
#15 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Do not forget that we can solve the problem by prescribing enterely and only BC.s in terms of velocity, without any BC for the pressure...This also shows that the pressure is an "auxiliary" variable.
|
|
|
|

|
|
|
|
|
#16 | |
|
New Member
Join Date: Dec 2015
Posts: 27
Rep Power: 10  |
Quote:
|
||
|
|

|
||
|
|
|
#17 | |
|
Senior Member
|
Quote:
 What I wrote in the first part is about something that happens when you solve NS equations in spectral space (so we are talking here about a very specific, 3D periodic and homogeneous case). In that case, you can rewrite the convective term so that the part balanced by the pressure gradient is already filtered out. In practice, the momentum equation ends up being without both the pressure gradient and a part of the convective term, because they always balance each other. It is shown very well in the book of Pope, Turbulent Flows, chapter 6, paragraph 6.4.2, page 213. Now, as stated, this does not usually comes out in discussions on the pressure role, so I have no reference stating what I'm stating here. However, if you look at the equations in that page, there really is nothing to prove, the pressure gradient exactly, and constantly in time, balances a part of the convective term (the one parallel to wavenumber vector, see eq. 6.142 in the book). Just as a sidenote, the Taylor-Green vortex solution is one where you can see this clearly happening in physical space, but the remaining part of the convective term is null in this case. So, for this solution, you also have that viscous and unsteady terms also perfecftly balance each other. The whole point here, I think, is agreeing on the fact that, even if I can choose a transformation that makes my pressure disappear from the equations, that doesn't actually affect the true pressure role. In the very specific case of my example this is also very apparent, because the resulting, pressure free, equations governing the evolution of the velocity field are not actually the same as the original equations. What followed in my post might look somehow more obscure, but what I meant, speculatively, is that, maybe, given the previous case, such role for the pressure can be spotted in other, less restrictive, cases or transformations. I cited the HH decomposition, on which FMDenaro produced a quite detailed paper, as an example. When the velocity field is splitted in a gradient and a curl part, it is only the gradient part that is affected by the pressure, not the curl part (take the curl of the incompressible momentum equations to see it). Still, differently from the spectral case, the curl part still needs the whole velocity field to be advected, so we either need to solve for the streamfunction or to correct the velocity field with the gradient part (which, accidentally, happens to be proportional to the pressure gradient to the lowest order). The whole point of my discussion was that there are several examples from which you can see that the role of the pressure is linked to a very specific part of the velocity field. In some cases you can arrange things so that that very specific part is not anymore responsible for advancing the whole velocity in time (the spectral case). In less fortuitous cases you can't achieve the same exceptional result, but still see how the pressure is linked only to a very specific part of the velocity field. All of this, of course, has to be interpreted in relation to the pressure for fully incompressible flows, which has to be interpreted as a correction with respect to the background thermodynamic pressure. Such thermodynamic pressure only affects the divergence of the velocity field via its time derivative (again, see the paper above as a reference for this). Hope this is more clear. |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Pressure loss Velocity coupling | CFXMUFFIN | CFX | 1 | February 6, 2016 04:43 |
| Pressure drop using Superficial velocity and interstitial velocity | Tanjina | FLUENT | 0 | November 8, 2015 23:25 |
| UDF to set velocity and pressure in inlet | GerardX89 | Fluent UDF and Scheme Programming | 0 | July 16, 2012 10:15 |
| Pressure velocity coupling | L Raiyaz Ahamed | CFX | 1 | August 29, 2009 11:08 |
| what the result is negatif pressure at inlet | chong chee nan | FLUENT | 0 | December 29, 2001 05:13 |