 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Peter Maroul
Join Date: May 2018
Posts: 52
Rep Power: 8  |
Hello every body.
I study on the multi-phase & phase change flow simulation by the Front tracking model. It's noted in the papers that the front tracking is not mass conserved. In the other word, the mass imbalance in this solver, is natural. My questions are presented as follows: 1- Why doesn't this model solve multi-phase flows as mass conserved? 2- What is the remedy for this deficiency (weakness) ? Thanks in advance for any attention & advice. P.Maroul |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
The motion of the phase front is exactly that. It has nothing to do with mass. Front tracking methods are usually level-set methods, they are ballistic. Ballistic equations don't describe anything except the trajectory.
Mass conservation come from a separate equation (the continuity equation). First you need an equation that guarantees mass conservation (i.e. the continuity equation). Then your choice of solving the discretized equations must also support this. FEM for example breaks conservation in the discretized equations, FVM preserves the conservation. Too often someone says something about oranges and somehow apples are involved. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
|
Not an expert on this but, on a general level, conservation of stuff (mass, momentum, etc.) is not guaranteed whenever it depends on interpolation.
As for the LuckyTran example, FE (and FD) methods do not typically discretize conservation equations, while FV methods do (and conservation is discretely fullfilled at any grid resolution). In the multiphase world, VOF methods actually discretize mass conservation equations while, in contrast, Level Set ones (and front tracking ones by extension) discretize, somehow, the domain of the phases and interpolations are involved on the boundaries between them. |
|
|
|

|
|
|
|
|
#4 |
|
Member
Peter Maroul
Join Date: May 2018
Posts: 52
Rep Power: 8  |
Dear Sirs.
Therefore-Based on your explanations-if I use FVM, the solution will be mass conserved. won't it? Is it enough? |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Join Date: Dec 2017
Posts: 153
Rep Power: 8  |
Hi, sbaffini is right! Level set is not mass conserving even in fvm. You need a special procedure called re-initialization to improve mass conservation. VoF is conservative but badley evaluate curvature giving raise to spurious currents (which you can correct with special force balanced methods). Thus as usally happens, the blanket is always short ��
Last edited by AliE; December 8, 2018 at 08:59. |
|
|
|

|
|
|
|
|
#7 | |
|
Member
Peter Maroul
Join Date: May 2018
Posts: 52
Rep Power: 8  |
Quote:
|
||
|
|

|
||
|
|
|
#8 | |
|
Member
Peter Maroul
Join Date: May 2018
Posts: 52
Rep Power: 8  |
Quote:
|
||
|
|

|
||
|
|
|
#9 |
|
Senior Member
Join Date: Dec 2017
Posts: 153
Rep Power: 8  |
If you are using level set method, yes or it can at least mitigate the problem. There are some papers in jcp about this procedure. For a good reference manual and more bibio, you can look also at the book on multiphase flows by tryggvason & prosperetti. Hightly reccomended for a nice overview!
|
|
|
|

|
|
|
|
|
#10 |
|
Member
Peter Maroul
Join Date: May 2018
Posts: 52
Rep Power: 8  |
Dear ALiE
I use the front tracking not Level Set. I imagine they are slightly different. Aren't they? What's the term jcp stand for? Would you plz indicate some papers only by paper address/number? Thanks anyway. |
|
|
|

|
|
|
|
|
#12 | |
|
Member
Peter Maroul
Join Date: May 2018
Posts: 52
Rep Power: 8  |
Quote:
I didn't find out the reason. I present mass continuity& mass transfer equations involved in the front tracking procedure and are probably the cause for the mass leak as follows:  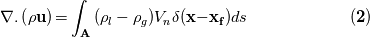 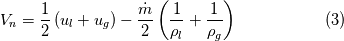 which above expression (equation) is responsible for the mass imbalance? Thanks for any answer. |
||
|
|

|
||
|
|
|
#13 |
|
Member
Peter Maroul
Join Date: May 2018
Posts: 52
Rep Power: 8  |
||
|
|

|
|
|
|
|
#14 | |
|
Senior Member
|
Quote:
You should follow the references backward starting from the source where you first read about the mass conservation issue and you will certainly find some that will go into the details. |
||
|
|

|
||
|
|
|
#15 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
The key of the problem is in Eq.(2) where the Dirac function is approximated on the discrete grid of finite size |
||
|
|

|
||
|
|
|
#16 |
|
Member
Peter Maroul
Join Date: May 2018
Posts: 52
Rep Power: 8  |
A fairly complete explanation of this topic is given in the paper "A Front-Tracking Method for the Computations
of Multiphase Flow by G. Tryggvason and et al" as follows " While the momentum equations are usually solved in the conservative from, the advection of the front is not conservative. Unlike the VOF method, for example, errors are likely to result in changes in the total mass. Accurate advection of the front points minimizes this error and we have done numerous simulations of bubbles, for example, where the change in mass remains within 1–2% during a time when the bubbles move about 100 diameters. In some cases, particularly for very long runs with many bubbles or drops where the resolution of each particle is relatively low, we have encountered changes in mass that are unacceptably high. In these cases, we correct the size of the particles every few time steps. Since the correction is very small at each time, the effect on the result is negligible. The inaccuracy in the advection of the front is due to errors coming from the interpolation of the velocities and the integration scheme. Increasing the accuracy of the front advection by using a higher order time stepping method is straightforward. The error due to the interpolation comes from the fact that although the discrete velocity field may be divergence-free (for incompressible flows), the interpolated velocity field is not necessarily divergence-free. An interpolation scheme that produces a divergence-free velocity at the front points has been developed by Peskin and Printz [89]. The result is, however, a more complex pressure equation, and we have not implemented this technique. Interpolation errors appear primarily to be due to poor resolution and should therefore generally be small. A test of the accuracy of the time integration has been done by Juric [59] who advected an initially circular blob of fluid by a prescribed velocity field that deformed the blob into a long ligament. Mass was conserved very well during the simulation and when the velocity was reversed, the circle was recovered nearly perfectly. This test has been used for several other methods that either track or capture interfaces, and it is generally found that tracking produces superior results. Adding and deleting front points and elements can also lead to changes in area and volume. However, by using a relatively large number of points and inserting points using a second-order curve fit, this effect is minimized." I have specified possible reasons for the mass leak as red colour. However, the real reason for mass leakage is still ambiguous for me. Thanks anyone for the more detailed description. |
|
|
|

|
|
|
|
|
#17 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Yes, I strongly suggest to read the series of papers of Peskin when the issue is analysed. The source of the error is the "interpolation" induced by the use of the discrete Dirac function
|
|
|
|

|
|
|
|
|
#18 |
|
Member
Join Date: Jul 2013
Posts: 56
Rep Power: 12  |
Touré, Fahsi and Soulaïmani (2016) proposed a level-set correction that extends the mass conservation of the method by constraining the level-set field to remain a signed distance function.
|
|
|
|

|
|
 |
| Tags |
| front tracking, mass conservation |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| mass flow rate not conserved in turbomachine, interface defined wrong? | wildli | FLUENT | 3 | September 15, 2022 12:19 |
| mass flow in is not equal to mass flow out | saii | CFX | 12 | March 19, 2018 05:21 |
| Multiphase flow - incorrect velocity on inlet | Mike_Tom | CFX | 6 | September 29, 2016 01:27 |
| Front capturing or tracking ? | Tony | Main CFD Forum | 10 | September 10, 2015 08:34 |
| Front tracking | Don Hawken | Main CFD Forum | 1 | December 12, 1999 13:29 |