 |
|
|
[Sponsors] | |||||
linear vs quadratic triangle and divergence theorem |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Join Date: Oct 2011
Posts: 239
Rep Power: 16  |
Dear all,
In a classic 2D unstructured finite volume code with linear triangles, I always get using mid-point quadrature rule 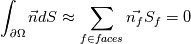 up to machine precision, where up to machine precision, where 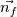 is unit normal and is unit normal and 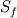 edge length. edge length.Now, let's say I have a triangle with two straight edges  and one "quadratic" edge and one "quadratic" edge 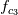 , e.g. a curved edge defined with three points: , e.g. a curved edge defined with three points: 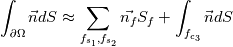 . .With 3 points defining my curved edge, I understand I can build a unique 2nd degree polynomial using Lagrange basis. Then I can approximate 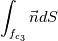 with a 3 points quadrature rule (Simpson if quadratic point is located at mid-distance). with a 3 points quadrature rule (Simpson if quadratic point is located at mid-distance).Problem is that numerical test gives me an integral which is not machine 0. With straight triangle edges, I understand mid-point rule is exact because the integrand is constant over the edge. In the same way, I expected Simpson's quadrature exact for 2nd degree polynomial and as such get 0 up to machine precision as well. Am I missing something or I possibly made a mistake in my numerical tests ? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
In what space is your curve defined. Perhaps you are confusing different reference spaces
 . If your curve is a polynomial (quadratic) in . If your curve is a polynomial (quadratic) in  and and 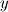 it might not be in it might not be in  and and 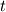 . .Note that the Jacobian determinante is defined as: 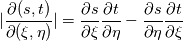 , ,or 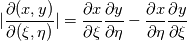 , ,or 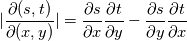 . .Regards Edit: I doubt that it is possible to integrate 2-D curved elements (quadratic) with a simple Simpson rule. The 2-D case is different to the 1-D case. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Oct 2011
Posts: 239
Rep Power: 16  |
Thank you for your reply !
You are certainly right, I am confusing something for sure. Let's say I have a straight triangle. I manually set 3 extra points somewhere in each edge bisector. This way, my "curved edges" are circle arcs and my "quadratic points" are at equal distance to the vertices of the triangle. Now I apply the quadrature along the three circle arcs. For each curved edges, I have three unit normals poiting outwards along the line joining the center to each nodes, the circle arc length and 1/6-4/6-1/6 weights. If I sum up these for the three edges, result is not 0. Last edited by naffrancois; October 9, 2020 at 07:57. Reason: image |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
Are the normal vectors taken from the exact circle?
For a consistent integration you should take the normals given by the quadratic approximation. They are not identical. This might result in an integration error and therefore in geometric aliasing. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Join Date: Oct 2011
Posts: 239
Rep Power: 16  |
The normal vectors are indeed taken from the exact circle arcs.
For each edge, I simply compute from the 3 points (let's say index 1 and 2 are vertices and 3 the extra point) the center and radius of the circle arc passing through the points. Then the normals are just 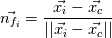 . . Length of circle arc is obtained from radius, center and vertices coordinates as 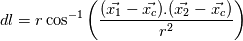 For each edge, I simply apply: 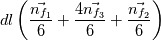 Well... in fact neither 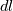 nor nor  are polynomials in x and y, is it in line with what you suggested in your first post ? May I conclude that the error I get on the integration is due to this fact ? are polynomials in x and y, is it in line with what you suggested in your first post ? May I conclude that the error I get on the integration is due to this fact ?
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
The first step would be to calculate all lengths and derivatives (normals and tangentials) from your polynomial quadratic approximation. Because these are the correct metrics if you consider three points for each curve.
I am quite sure with this it should work. The only problem is, that you mix different metrics. Simply be aware that you do not integrate the exact circle with three points. Otherwise you would have to use a number of infinity collocation points. |
|
|
|

|
|
|
|
|
#7 | |
|
Senior Member
Join Date: Oct 2011
Posts: 239
Rep Power: 16  |
Quote:
On the other hand, let's say now I exclusively work with a polynomial representation of my curved edges, from which I extract lengths and derivatives to compute the normals. Then if this polynomial can be integrated exactly by the quadrature rule, then I would recover sum nds=0. Many thanks for your help ! |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
Yes! If you are considering nodal basis functions (Lagrange kernels) the only possibility is to increase the number of points respectively the uniquely linked quadrature rule.
You may also consider other basis functions, e.g. modal ones. With them you easily can integrate the circle exact with only one mode. However, in practice you are not able to describe arbitrary geometry shapes with algebraic functions. Regards |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Join Date: Oct 2011
Posts: 239
Rep Power: 16  |
Many thanks for your answers, now I can go on

|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,773
Rep Power: 71    |
I read only the original question, not the replies so I can be quite junk in my answer.
I want to stress an issue... The Simpson rule is exact for a 1D homogeneous distribution of nodes and a quadratic function, that is something like Int[a,b] x^2 dx should be exactly computed by Simpson. That means you have to transform you curved edge in a computational plane where it is a straight edge and you apply Simpson. But when you go back to the physical plane you have the metric. Is that the problem you are discussing? |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Join Date: Oct 2011
Posts: 239
Rep Power: 16  |
Thank you FMDenaro for your input. After the intervention of Eifoehn4 I thought I conceptually moved forward in the understanding but I am confused again. I feel I miss some concepts of calculus.
I will restate the problem. I have a 2D unstructured mesh composed of quadratic triangles, e.g. 6 nodes triangles. I use a finite volume code so I need area of element as well as length of edges and normals. I want to apply a high order flux integration over the edges so I need the normals at different locations on the edges. Obviously if edges are straight, no problem. Let's imagine a general quadratic triangle where "mid points" does not lie on the segments formed by the vertices. What I have are x,y coordinates of the 6 triangle nodes, given by gmsh. At first I thought of a naive approach: constructing circle arcs for each edge passing through the 3 nodes. This way I could easily compute length of curved edges, area of element and normals. Problem occured when trying to apply 3 points quadrature integration per edge to compute 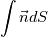 . I do not get 0. As explained by Eifoehn4, if I understood correctly, this is because I am trying to integrate a circle arc which cannot be written as a 2nd order polynomial in an explicit form as y=f(x). If I increase the number of nodes in the quadrature the approximation of . I do not get 0. As explained by Eifoehn4, if I understood correctly, this is because I am trying to integrate a circle arc which cannot be written as a 2nd order polynomial in an explicit form as y=f(x). If I increase the number of nodes in the quadrature the approximation of 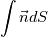 tends to 0, which makes sense. tends to 0, which makes sense.So now I follow a different approach by constructing for each edge a quadratic polynomial 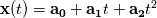 passing by the 3 nodes. But to compute curved edge length I think I need to evaluate the integral passing by the 3 nodes. But to compute curved edge length I think I need to evaluate the integral 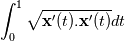 . This integral seems to have a rather complicated analytic expression, then I guess I would have to integrate it numerically as well using a pretty high quadrature rule. Next, with the curved edges lengths in hand I thought of simply applying 3 points quadrature rule (assuming third node is located at mid distance on the curve this is Simpson, otherwise I have to calculate different weights) to compute . This integral seems to have a rather complicated analytic expression, then I guess I would have to integrate it numerically as well using a pretty high quadrature rule. Next, with the curved edges lengths in hand I thought of simply applying 3 points quadrature rule (assuming third node is located at mid distance on the curve this is Simpson, otherwise I have to calculate different weights) to compute 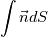 . .Do you think this is the way to go or would you have some references to read ? Many thanks for your help and advice ! |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
Are you familiar with the creation of interpolation and differentiation matrices on triangles for arbitrary polynomial degrees?
|
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,773
Rep Power: 71    |
Quote:
Maybe you can find some suggestions here https://www.researchgate.net/publica...mulation_codes https://www.researchgate.net/publica...ructured_grids |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Join Date: Oct 2011
Posts: 239
Rep Power: 16  |
Hello Eifoehn4,
Long time ago when I worked with structured boundary fitted grids I had to deal with grid metrics, mapping from physical->computational plane with chain rule and Jacobian. This is the furthest I went and I barely remember anything. Is this somehow related with your question ? |
|
|
|

|
|
|
|
|
#15 | |
|
Senior Member
Join Date: Oct 2011
Posts: 239
Rep Power: 16  |
Quote:
Thank you for the suggestions, I will have a look. |
||
|
|

|
||
|
|
|
#16 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
Quote:
__________________
Check out my side project: A multiphysics discontinuous Galerkin framework: Youtube, Gitlab. Last edited by Eifoehn4; October 12, 2020 at 09:12. |
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
Join Date: Oct 2011
Posts: 239
Rep Power: 16  |
Many thanks Eifoehn4 and FMDenaro for your help.
Thanks to your hints I could get it working for a single general quadratic triangle. I used one set of 2nd degree shape functions for the triangle in order to get the area. I used 3 sets of quadratic shape functions for the 3 curved segments to get edge integrals and normals. It turns out that triangle area, edges lengths and normals have all analytic expression using a 2nd degree Lagrange representation (edge length expression is a bit lengthy though). I checked that using a formal calculus software. I finally get 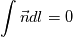 to machine precision using 3 points 1/6-4/6-1/6 quadrature on the mapped space. to machine precision using 3 points 1/6-4/6-1/6 quadrature on the mapped space.    edit: after reconsideration and following your comments I was doubtful about the exactness of simpson's rule, but under the 2nd degree mapping I get: ![\int_{\partial\Omega}\vec{n}dl=\sum_{f\in{1,3}}\left(\int_0^1\vec{n}_f(\xi)\sqrt{\left(\frac{\partial x_f}{\partial\xi}\right)^2+\left(\frac{\partial y_f}{\partial\xi}\right)^2}d\xi\right)=\sum_{f\in{1,3}}\left(\int_0^1\left[\frac{\partial y_f}{\partial\xi},-\frac{\partial x_f}{\partial\xi}\right]d\xi\right) \int_{\partial\Omega}\vec{n}dl=\sum_{f\in{1,3}}\left(\int_0^1\vec{n}_f(\xi)\sqrt{\left(\frac{\partial x_f}{\partial\xi}\right)^2+\left(\frac{\partial y_f}{\partial\xi}\right)^2}d\xi\right)=\sum_{f\in{1,3}}\left(\int_0^1\left[\frac{\partial y_f}{\partial\xi},-\frac{\partial x_f}{\partial\xi}\right]d\xi\right)](/Forums/vbLatex/img/511478c87d327ad6d5b7947c3b437b35-1.gif) . The integrand is linear so the 3 points rule is exact . The integrand is linear so the 3 points rule is exact
Last edited by naffrancois; October 15, 2020 at 05:42. |
|
|
|

|
|
|
|
|
#18 |
|
Super Moderator
|
Quote:
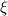 would be exact !!! would be exact !!!
|
|
|
|

|
|
|
|
|
#19 |
|
New Member
Join Date: Oct 2020
Posts: 2
Rep Power: 0  |
Last edited by blancot; October 27, 2020 at 13:09. |
|
|
|

|
|
|
|
|
#20 |
|
New Member
gail jacob
Join Date: Sep 2021
Posts: 1
Rep Power: 0  |
Bear in mind that, for a given number of elements, quadratic elements allow better representation of a curved boundary.
paperwritingservice |
|
|
|

|
|
 |
|
|