 |
|
|
[Sponsors] | |||||
Discrete Adjoint derivative computation - help understanding Finite Difference |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
topheruk
Join Date: Mar 2018
Posts: 5
Rep Power: 8  |
I am looking for some guidance on the implementation of the Discrete Adjoint method, specifically the computation of the partial derivatives via Finite Differencing.
source(s): DAFoam: An Open-Source Adjoint Framework for Multidisciplinary Design Optimization with OpenFOAM https://arc.aiaa.org/doi/10.2514/1.J058853 The first major step in solving the Discrete Adjoint is computing the partial derivatives of the vector of flow residuals ( 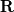 ) with respect to the vector state variables ( ) with respect to the vector state variables (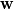 ). This is possible via Finite Difference: ). This is possible via Finite Difference:Set ![\textbf{w}=[u,v,w,p,\nu,\phi] \textbf{w}=[u,v,w,p,\nu,\phi]](/Forums/vbLatex/img/a3462954911bec7812d80d7569ac8f9c-1.gif) and and ![\textbf{R}=[R_u,R_v,R_w,R_p,R_\nu,R_\phi] \textbf{R}=[R_u,R_v,R_w,R_p,R_\nu,R_\phi]](/Forums/vbLatex/img/377ae71a3dcce14ff24686f21096d61c-1.gif) , ,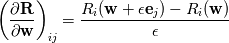 where the subscripts 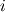 and and 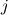 are the row and column indices, respectively, are the row and column indices, respectively,  is the step size, and is the step size, and 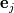 is a unit vector with unity in row is a unit vector with unity in row 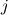 . As I understand it, this involves sequentially perturbing each element of the state variable vector in a reference cell and recomputing the residual vector. This should produce a . As I understand it, this involves sequentially perturbing each element of the state variable vector in a reference cell and recomputing the residual vector. This should produce a 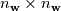 matrix, with matrix, with 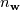 calls to residual function (equal to the number of columns). Is this correct? calls to residual function (equal to the number of columns). Is this correct?In the DAFoam implementation, a graph-colouring method is used to accelerate the computation of the partial derivatives via Finite Difference. This works by exploiting the sparsity of a Jacobian matrix to simultaneously perturb sets of columns that influence independent rows. An example is given for a 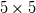 diagonal Jacobian matrix but I am not sure what step this relates to in the context of computing the partial derivates for diagonal Jacobian matrix but I am not sure what step this relates to in the context of computing the partial derivates for 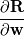 , particularly for a 3D problem. , particularly for a 3D problem.Assumptions: 1. For an unperturbed and converged flow solution, each cell contains a 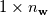 vector of flow variables and a vector of flow variables and a 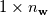 vector of residuals. vector of residuals.Questions: 1. when the source(s) discusses graph-colouring, what matrix are they referring to? Is the 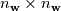 Jacobian of Jacobian of 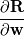 in each cell? in each cell?2. when perturbing a flow variable e.g. the u-component of velocity, is  added to the reference value in a specific cell only, or does this perturbation affect the reference values in neighbouring cells? added to the reference value in a specific cell only, or does this perturbation affect the reference values in neighbouring cells?3. how does perturbing a flow variable in a cell influence other rows in the matrix? Appreciate any input, Chris Last edited by topheruk29; July 21, 2021 at 06:57. Reason: missed out vector definitions |
|
|
|

|
|
 |
| Tags |
| adjoint, mathematics, optimization |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| The adjoint equation in the discrete adjoint solver | Zhen ZHANG | SU2 | 3 | July 16, 2021 07:59 |
| Nonlinear derivative in finite difference | BoxQwerty | Main CFD Forum | 2 | February 23, 2021 12:49 |
| Fixed CL Mode and Discrete Adjoint Question | Parth Kumar | SU2 | 0 | January 29, 2020 22:30 |
| Direct derivatives | kmandar | SU2 | 12 | May 2, 2016 15:18 |
| finite difference method for navier-stokes problem | dallybird | Main CFD Forum | 5 | February 17, 2003 22:00 |